Пример 1

Определить допустимый ток для медной шины, поперечное сечение которой 120×10 мм. Шина установлена на ребро в спокойном воздухе горизонтально. Частота переменного тока f=50 Гц, допустимая температура нагрева шины Т_доп=85 ºС, температура окружающей среды Т_о=35 ºС.

Решение

Тепловая энергия, выделяющаяся в проводнике при протекании по нему тока, должна отводиться в окружающую среду с поверхности:

(1+ )

где

Вт/(м²·К).

Тогда I²·1,62·10^-8(1+0,004385) ·

где F=0,12·1·2+0,01·1·2=0,26 м² – площадь боковой поверхности шины длиной 1 м; S=0,12·0,01=0,0012 м² – площадь поперечного сечения шины; α=0,0043 – температурный коэффициент сопротивления, К^-1.

Таким образом, допустимый ток I=0,3·10⁴ А.

Пример 2

Определить длительно допустимое значение плотности переменного тока для цилиндрической катушки индуктивности, которая намотана проводом d=2 мм, имеет число витков W=500, наружный диаметр D_нар=136 мм, внутренний D_вн=70 мм, ее высота h=72 мм и допустимая температура нагрева Т_доп=90 ºС.

Решение

Уравнение баланса тепловой энергии, выделяющейся в теле катушки и отводимой с ее поверхности,

где α=0,0043 К^-1; Т_о=35 ºС – температура окружающей среды; F=3,14(136+70)·72·10^-6+2·3,14(136²-70²)·10^-6/4=0,067 м² – теплоотдающая поверхность катушки; l_ср=π(D_нар+D_вн)/2=3,14(136+70) )·10^-3/2=0,323 м – средняя длина витка катушки; ρ_о=1,62·10^-8 Ом·м;

К_T=3,6[1+0,005(T_доп-Т_о)] Вт/(м²·К).

Полагая коэффициент поверхностного эффекта k_п=1, плотность тока определим как

А/м².

Пример 3

Составить уравнение кривой нагрева алюминиевой шины прямоугольного поперечного сечения 100×100 мм, если в момент времени t=0 она нагружается постоянным током I=2000 А. В начальный момент времени температура шины Т₀=50 ºС, температура окружающего воздуха Т₀=35 ºС, коэффициент теплоотдачи с наружной поверхности шины k_т=20 Вт/(м²·К). При расчете учесть изменение удельного сопротивления алюминия от температуры.

Решение

Для алюминия Ом·м; α=0,0042 К^-1; λ=210 Вт/(м·К) – коэффициент теплопроводности; с=950 Дж/(кг·К) – удельная теплоемкость; γ=2700 кг/м³. Зависимость температуры токоведущей части электрического аппарата от температуры в процессе нагрева определяется по следующему выражению:

,

где Т_уст, Т_нач – установившееся и начальное значения температуры,

Т_уст=

где , если длина шины l=1 м,

ºС;

– площадь теплоотдачи поверхности шины; S=0,1·0,01=10^-3 м² – площадь сечения шины.

Определяем постоянную времени:

с,

где m – масса шины длиной 1 м; P_o=4·10⁶·2,62·10^-8· =105 Вт.

Тогда уравнение кривой нагрева будет иметь вид

.

Пример 4

Вычислить время, через которое медная труба с поперечными размерами d_вн=25 мм, d_нар=30 мм нагреется до температуры t=110 ºС в результате протекания тока I=9400 А. С целью охлаждения по трубе протекает вода, средняя температура которой t_ср=40 ºС. Коэффициент теплоотдачи с внутренней поверхности трубы k_т=1500 Вт/(м²·К). Удельное сопротивление меди ρ=1,75·10^-8 Ом·м.

Решение

Уравнение нагрева электропроводящей части электрического аппарата до заданной температуры имеет вид

T=T_уст где T_уст= ,

где F=πd_вн·1=3,14·25·10^-3·1=78,5·10^-3 м² – теплоотдающая внутренняя поверхность трубы;

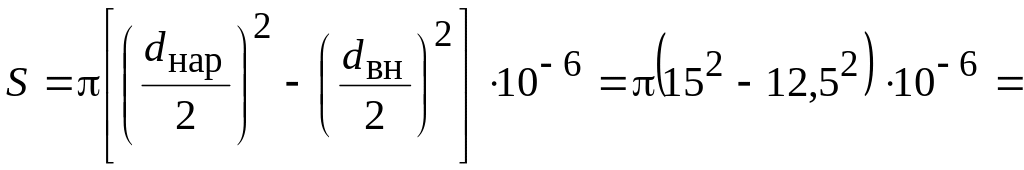
– площадь поперечного сечения трубы; α=0,0043 К^-1;

Так как ›› , то постоянную времени находим по формуле

с,

где т= γ·v=γSl·8700216∙10^-6·1=1,88 кг; γ=8700 кг/м³; с=390 Дж/(кг·К) – удельная теплоемкость.

Установившееся значение температуры будет равно

Подставив полученные значения в первоначальную формулу, получим

или откуда t=10,3 с.