12. Последовательность этапов практической реализации алгоритмов симплекс-метода при решении задач линейного программирования.

Алгоритм симплексного метода решения задач линейного программирования

Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:

• Привести задачу к каноническому вид

• Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)

• Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода

• Если выполняется признак единственности оптимального решения, то решение задачи заканчивается

• Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения

13.Двойственная задача лп.

Рассмотрим основные понятия и выводы специального

раздела линейного программирования — теорию двойственности.

В гл. 2 показано, что любую задачу линейного программирования

можно записать следующим образом:

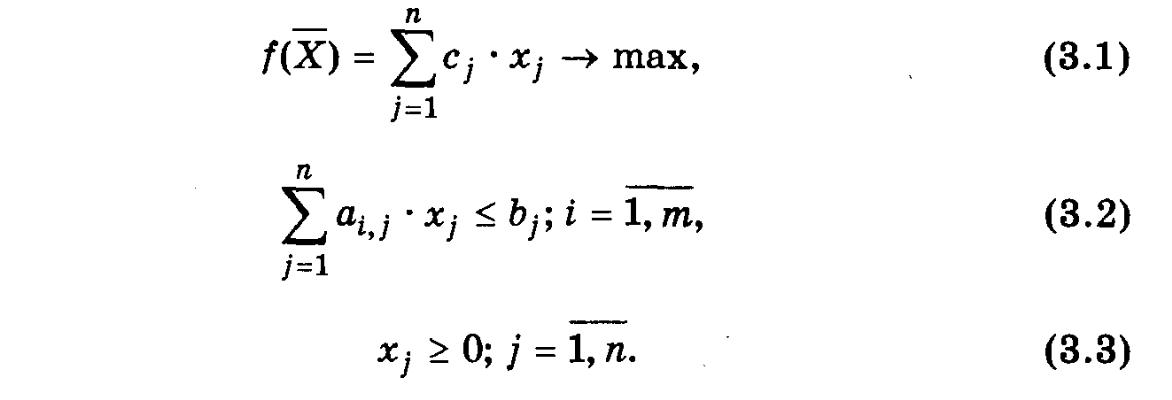
В этой главе для большей наглядности используются

записи типа f(X) -» max(min).

С каждой задачей линейного программирования тесно

связана другая линейная задача, называемая двойственной;

первоначальная задача называется исходной или прямой.

Связь исходной и двойственной задач заключается, в частности,

в том, что решение одной из них может быть получено

непосредственно из решения другой.

Хорошо разработанный математический аппарат линейного

программирования позволяет не только получать с помощью

эффективных вычислительных процедур оптимальный

план, но и делать ряд экономически содержательных выводов,

основанных на свойствах задачи, двойственной к исходной

ЗЛП. Переменные двойственной задачи у; называют объективно

обусловленными оценками., или двойственными оценками.

Модель двойственной задачи имеет вид:

Каждая из задач двойственной пары фактически является

самостоятельной задачей линейного программирования и

может быть решена независимо от другой. Однако при определении

симплексным методом оптимального плана одной

из задач находится решение и другой задачи.

Двойственная задача по отношению к исходной составляется

согласно следующим правилам:

1) целевая функция исходной задачи (3.1)-(3.3) формулируется

на максимум, а целевая функция двойственной

задачи (3.4)-(3. 6) — на минимум, при этом в задаче на

максимум все неравенства в функциональных ограничениях

имеют вид <,= а в задаче на минимум — вид >=;

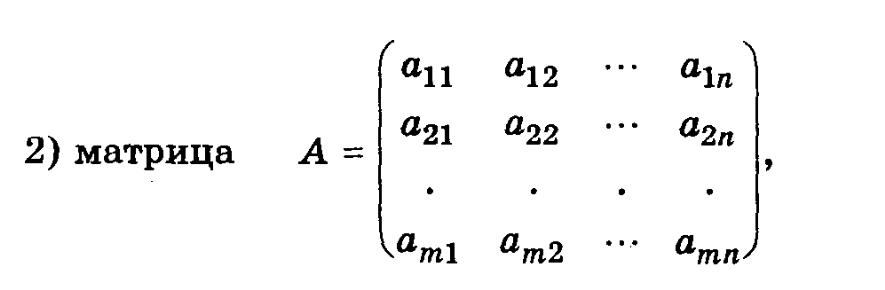
составленная из коэффициентов при неизвестных в системе

ограничений (3.2) исходной задачи, и аналогичная матрица

в двойственной задаче получаются друг из друга транспонированием

3) число переменных в двойственной задаче равно числу

функциональных ограничений (3.2) исходной задачи, а

число ограничений в системе (3.5) двойственной задачи —

числу переменных в исходной задаче;

4) коэффициентами при неизвестных в целевой функции

(3.4) двойственной задачи являются свободные члены в

системе (3.2) ограничений исходной задачи, а правыми

частями в ограничениях (3.5) двойственной задачи —

коэффициенты при неизвестных в целевой функции (3.1)

исходной задачи;

5) каждому ограничению одной задачи соответствует переменная

другой задачи: номер переменной совпадает с

номером ограничения; при этом ограничению, записанному

в виде неравенства <, соответствует переменная,

связанная условием неотрицательности. Если функциональное

ограничение исходной задачи является равенством,

то соответствующая переменная двойственной задачи

может принимать как положительные, так и отрицательные

значения.

Математические модели пары двойственных задач могут

быть симметричными и несимметричными. В несимметричных

двойственных задачах система ограничений исходной

задачи задается в виде равенств, а двойственной — в виде

неравенств, причем в последней переменные могут быть и

отрицательными. В симметричных задачах система ограничений

как исходной, так и двойственной задачи задается

неравенствами, причем на двойственные переменные налагается

условие неотрицательности.

Итак, согласно теории линейного программирования каждой

ЗЛП вида (3.1)-(3.3) соответствует двойственная ей

ЗЛП: (3.4)-(3.6).