4. Принцип оптимальности в планировании и управлении.

5. Общая задача оптимального программирования.

6. Классификация задач оптимального программирования.

Линейное программирование — это частный раздел оптимального

программирования. В свою очередь оптимальное

(математическое) программирование — раздел прикладной

математики, изучающий задачи условной оптимизации. В

экономике такие задачи возникают при практической реали-

-зации принципа оптимальности в планировании и управлении.

Необходимым условием использования оптимального

подхода к планированию и управлению (принципа оптимальности)

является гибкость, альтернативность производственно-

хозяйственных ситуаций, в условиях которых приходится

принимать планово-управленческие решения. Именно

такие ситуации, как правило, и составляют повседневную

практику хозяйствующего субъекта (выбор производственной

программы, прикрепление к поставщикам, маршрутизация,

раскрой материалов, приготовление смесей и т.д.).

Суть принципа оптимальности состоит в стремлении выбрать

такое планово-управленческое решение X = (Х1, Х2… Хп), где

Хj, (j = 1, п ) — его компоненты, которое наилучшим образом

учитывало бы внутренние возможности и внешние условия

производственной деятельности хозяйствующего субъекта.

Слова «наилучшим образом» здесь означают выбор некоторого

критерия оптимальности, т.е. некоторого экономического

показателя, позволяющего сравнивать эффективность

тех или иных планово-управленческих решений. Традиционные

критерии оптимальности: «максимум прибыли», «минимум

затрат», «максимум рентабельности» и др.

Слова «учитывало бы внутренние возможности и внешние

условия производственной деятельности» означают, что

на выбор планово-управленческого решения (поведения) накладывается

ряд условий, т.е. выбор X осуществляется из

некоторой области возможных (допустимых) решений D;

эту область называют также областью определения задачи.

Таким образом, реализовать на практике принцип оптимальности

в планировании и управлении — это значит решить

экстремальную задачу вида:

Условие (2.5) необязательно, но его всегда при необходимости

можно добиться. Обозначение [<,=,>} говорит о том,

что в конкретном ограничении возможен один из знаков:

<,= или >. Более компактная запись:

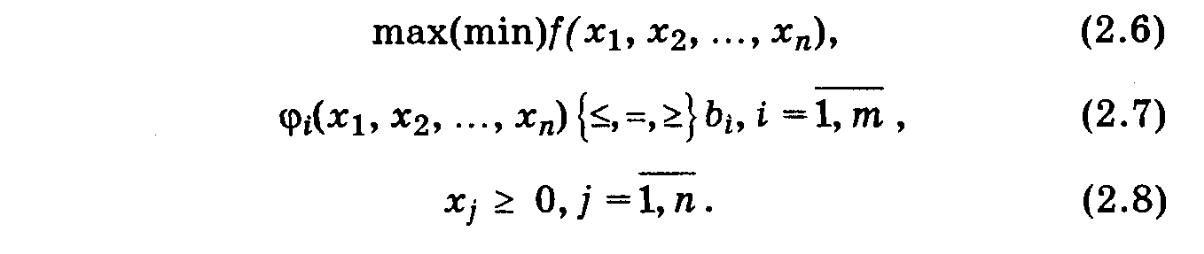Задача (2.6)-(2.8) — общая задача оптимального (математического)

программирования, иначе — математическая

модель задачи оптимального программирования, в основе

построения (разработки) которой лежат принципы оптимальности

и системности.

Вектор X (набор управляющих переменных Xj, j = 1, п )

называется допустимым решением, или планом задачи оптимального

программирования, если он удовлетворяет системе

ограничений. А тот план X (допустимое решение), который

доставляет максимум или минимум целевой функции

f(Х1, Х2 ..., хп), называется оптимальным планом (оптимальным

поведением, или просто решением) задачи оптимального

программирования.

Таким образом, выбор оптимального управленческого поведения

в конкретной производственной ситуации связан с

проведением с позиций системности и оптимальности экономико-

математического моделирования и решением задачи

оптимального программирования.

Задачи оптимального программирования в наиболее общем

виде классифицируют по следующим признакам.

1. По х а р а к т е р у в з а и м о с в я з и между

п е р е м е н н ы м и —

а) линейные,

б) нелинейные.

В случае а) все функциональные связи в системе ограничений

и функция цели — линейные функции; наличие нелинейности

хотя бы в одном из упомянутых элементов приводит

к случаю б).

2. По х а р а к т е р у и з м е н е н и я п е р е м е н н

ы х —

а) непрерывные,

б) дискретные.

В случае а) значения каждой из управляющих переменных

могут заполнять сплошь некоторую область действительных

чисел; в случае б) все или хотя бы одна переменная

могут принимать только целочисленные значения.

3. По у ч е т у ф а к т о р а в р е м е н и —

а) статические,

б) динамические.

В задачах а) моделирование и принятие решений осуществляются

в предположении о независимости от времени

элементов модели в течение периода времени, на который

принимаетсяпланово-управленческое решение. В случае б)

такое предположение достаточно аргументированно принято

не может быть и необходимо учитывать фактор времени.

4. По н а л и ч и ю и н ф о р м а ц и и о п е р е м е н н

ы х —

а) задачи в условиях полной определенности (детерминированные),

б) задачи в условиях неполной информации,

в) задачи в условиях неопределенности.

В задачах б) отдельные элементы являются вероятностными

величинами, однако известны или дополнительными

статистическими исследованиями могут быть установлены

их законы распределения. В случае в) можно сделать предположение

о возможных исходах случайных элементов, но

нет возможности сделать вывод о вероятностях исходов.

5. П о ч и с л у к р и т е р и е в о ц е н к и а л ь т е р на т и в —

а) простые, однокритериальные задачи,

б) сложные, многокритериальные задачи.

В задачах а) экономически приемлемо использование одного

критерия оптимальности или удается специальными

процедурами (например, «взвешиванием приоритетов») свести

многокритериальный поиск к однокритериальному; примеры

многокритериальных задач рассмотрены в гл. 3.

Сочетание признаков 1—5 позволяет группировать (классифицировать)

в самом общем виде задачи и методы оптимального

программирования, например: 1а)2а)3а)4а)5а) —

задачи и методы линейного программирования, 1б)2а)3а)

4а)5а) — задачи и методы нелинейного программирования,

1а)2б)3а)4а)5а) — задачи и методы целочисленного (дискретного)

линейного программирования и т.д.