46. Задачі багатокритеріальної оптимізації.

Многокритериальные задачи оптимизации являются, пожалуй, самым молодым направлением экстремального управления. Основной проблемой здесь является изыскание эффективных способов введения дополнительной информации, которая необходима для отыскания единственного решения. Многокритериальная задача оптимизации в методе обратного распространения рассматривается как набор однокритериаль-ных - на каждой итерации происходят изменения значений параметров сети, улучшающие работу лишь с одним примером обучающей выборки. Такой подход существенно уменьшает скорость обучения. В многокритериальных задачах оптимизации проблема формирования эвристик часто решается довольно просто: каждое правило должно соответствовать одному из имеющихся критериев оптимальности. В многокритериальных задачах оптимизации или задачах векторной оптимизации множеству критериев соответствует и множество функций цели, сформулированных перед системой управления, которые математически могут выражаться линейными или нелинейными функционалами. Важный класс многокритериальных задач оптимизации составляют те задачи, в которых между критериями существуют отношения предпочтения, не фиксированные жестко. Этот класс задач решается методом последовательных уступок. Стратегия решения многокритериальной задачи оптимизации при использовании аддитивной целевой функции имеет серьезный недостаток, который обусловлен конфликтностью критериев. Максиминная стратегия решения многокритериальных задач оптимизации нацелена на максимальное удовлетворение технических требований, предъявляемых к объекту проектирования. При использовании максиминной стратегии решения многокритериальной задачи оптимизации затраты времени на анализ чувствительности еще более возрастают, так как в этом случае целевой функцией на различных шагах поиска может оказаться функция любого из критериев. Рассмотрена проблема принятия решения в многопараметрической и многокритериальной задаче оптимизации, когда веса целевых функций неизвестны либо одинаковы. Предложен способ принятия решения, основанный на анализе многомерной таблицы испытаний. Один из наиболее часто применяемых подходов к решению многокритериальной задачи оптимизации состоит в сведении ее к однокритериальной посредством агрегирования в одном критерии нескольких показателей качества со своими весовыми коэффициентами или путем выделения наиболее важного показателя в качестве единственного критерия с переводом остальных показателей в разряд ограничений. изации.

Постановка задачи многокритериальной оптимизации.

Будем называть каждый из скалярных критериев оптимальности частным критерием оптимальности. Совокупность частных критериев оптимальности будем называть векторным критерием оптимальности. Положим, что ставится задача минимизации каждого из частных критериев оптимальности ф₁( ), ф₂( ), ... , ф_s( ) в одной и той же области допустимых значений .

Решение задачи многокритериальной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, а оказывается некоторым компромиссом для вектора в целом.

Задачу многокритериальной оптимизации будем записывать в виде

(1)

где — множество допустимых значений вектора варьируемых параметров .

Прежде, чем применить тот или иной метод решения задачи (1), обычно производят нормализацию частных критериев, приводя все частные критерии оптимальности к одному масштабу. Чаще всего при этом используют относительные отклонения частных критериев от их минимальных значений:

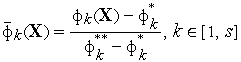
где

Метод относится к классу стохастических методов оптимизации

Сохраним за нормализованными частными критериями оптимальности обозначения .