
- •Федеральное агентство по образованию
- •1.Системы линейных алгебраических уравнений
- •1.1. Основные понятия и определения
- •1.2.Методы решения систем линейных уравнений
- •1.2.1.Метод Крамера
- •Замечание. Если главный определитель системы отличен от нуля 0, то система имеет единственное решение.
- •1.2.2.Матричный метод
- •Эту систему можно записать в матричном виде с помощью матричного уравнения
- •1.2.3 Метод Гаусса
- •Полученная матрица соответствует системе
- •1.3 Задачи для самостоятельного решения
- •1.4. Вопросы для подготовки к экзамену по теме «Системы линейных алгебраических уравнений»
- •2. Комплексные числа
- •2.1.Понятие и представления комплексных чисел
- •2.2.Формы записи комплексных чисел
- •2.3.Действия над комплексными числами
- •2.4 Задачи для самостоятельного решения
- •2.5 Вопросы для подготовки к экзамену по теме «Комплексные числа»
- •3. Линейные преобразования собственные значения и собственные векторы
- •Задачи для самостоятельного решения
- •Оглавление
- •Библиографический список
- •660025, Г. Красноярск, ул. Вавилова, 66 а
- •660025, Г. Красноярск, ул. Вавилова, 66 а
1.2.3 Метод Гаусса
Одним из наиболее универсальных и эффективных методов решения систем линейных алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.
Рассмотрим систему (1)
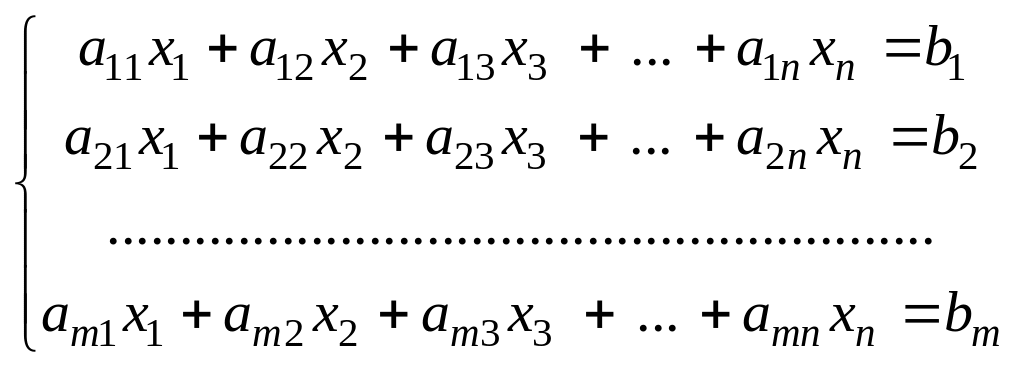 .
.
Процесс решения такой системы методом Гаусса состоит из трех этапов.
На первом этапе с помощью элементарных преобразований получают систему уравнений, эквивалентную системе (1). Другими словами систему (1) сводят к ступенчатому виду
 (7)
(7)
где
![]() -
коэффициенты при неизвестных и свободные
члены, полученные в результате элементарных
преобразований.
-
коэффициенты при неизвестных и свободные
члены, полученные в результате элементарных
преобразований.
На втором этапе исследуют систему линейных алгебраических уравнений, то есть определяют количество ее решений по теореме
Кронекера - Капелли.
Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы
![]() .
.
Правила практического поиска всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение
![]() .
.
Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений
![]() .
.
На третьем этапе последовательно находят все решения, начиная поиск неизвестных членов хi c последнего уравнения эквивалентной системы (7) .
Пример 3. Решить систему методом Гаусса:
 .
.
![]() Решение.
Переход к эквивалентной системе проведем
с помощью элементарных преобразований
расширенной матрицы заданной системы
уравнений (получим нули под главной
диагональю):
Решение.
Переход к эквивалентной системе проведем
с помощью элементарных преобразований
расширенной матрицы заданной системы
уравнений (получим нули под главной
диагональю):
 ~
~
 ~
~
 ~
~
 ~
~ .
.
Полученная матрица соответствует системе
 .
.
Ранг
расширенной матрицы
![]() =
=
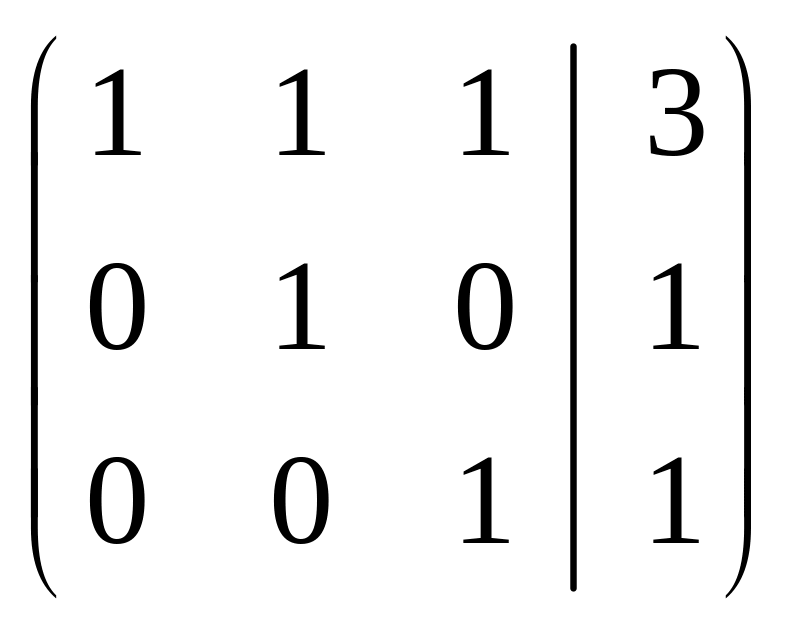 равен трем,
равен трем,
![]() ,
,
т.к. в ней содержится минор наивысшего третьего порядка, отличный от нуля
 ,
,
т.е. (матрица состоит из трех не нулевых строк).
Ранг
основной матрицы системы
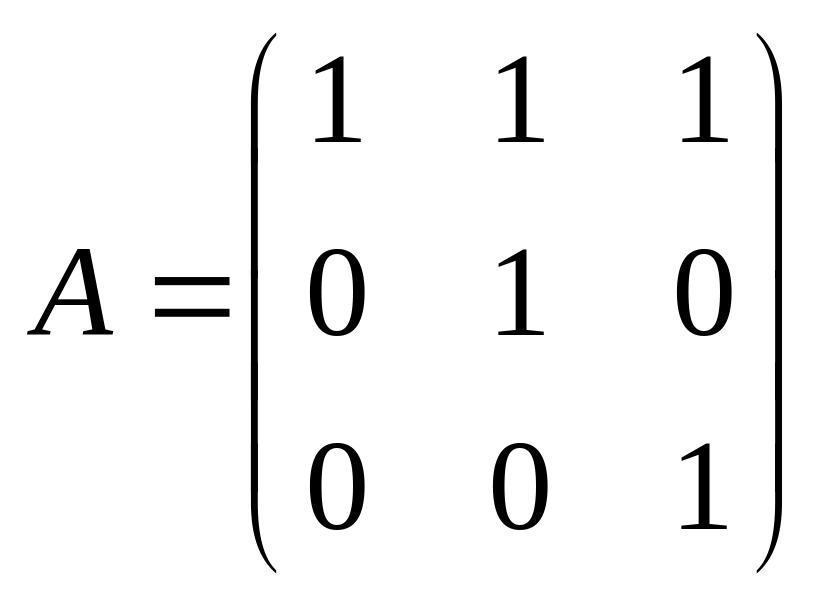 также равен трем
также равен трем
![]() .
.
Так как ранги расширенной и основной матрицы равны между собой и равны количеству неизвестных
![]() ,
,
то система уравнений имеет единственное решение.
Начиная с последнего уравнения системы найдем последовательно значения неизвестных х3, х2, х1:
х3 = 1,
х2 = 1,
х1 = 3 – х2 – х3 ,
откуда окончательно имеем решение системы х3 = 1, х2 = 1, х1 = 1.
Ответ. (1,1,1).
Пример 4. Решить систему методом Гаусса:
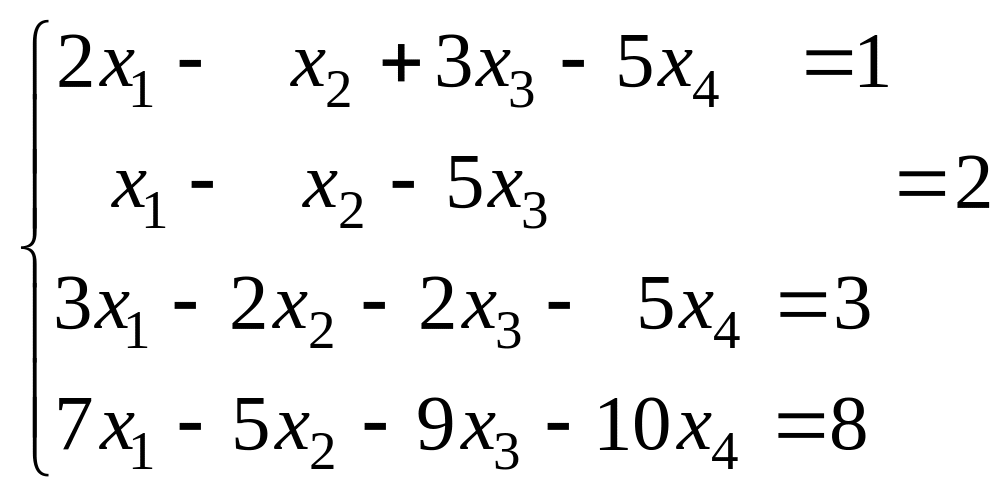 .
.
Решение. Составим расширенную матрицу системы и обнулим с помощью элементарных преобразований элементы, стоящие под главной диагональю:
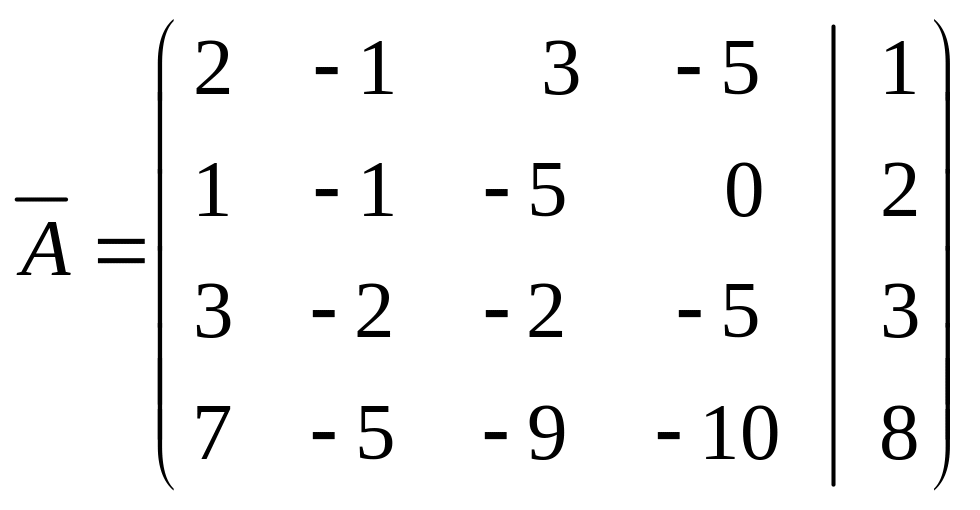 ~
~ ~
~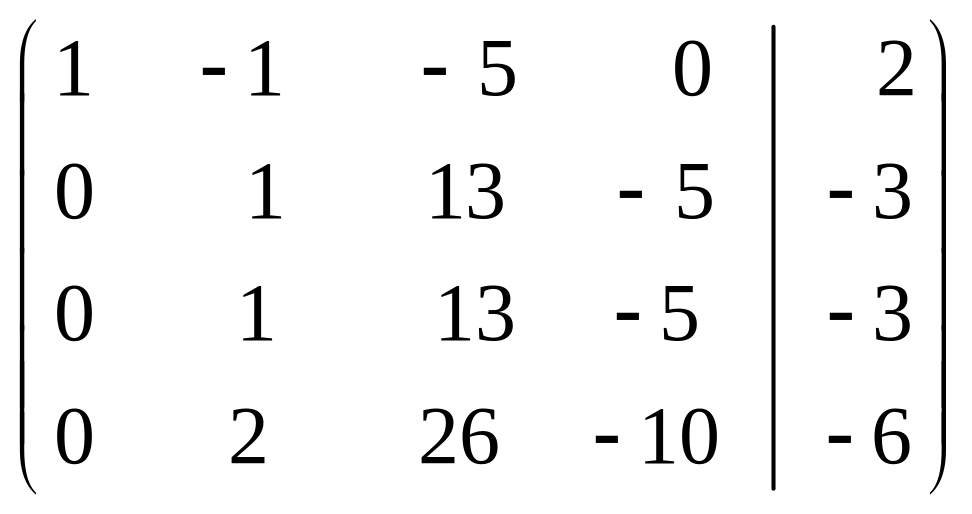 ~
~ ~
~![]() .
.
Составим эквивалентную систему
![]()
и определим количество ее решений:
ранг расширенной матрицы
 равен двум
равен двум
 ,
т.к.
,
т.к.
 ,
,ранг основной матрицы системы
 равен двум
равен двум
 ,
т.к.
,
т.к.
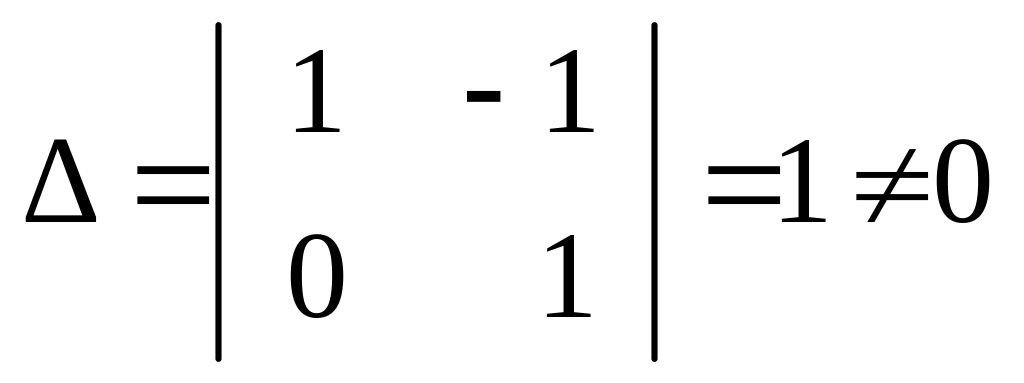 ,
,количество неизвестных хi равно четырем n = 4.
Так
как выполнено условие
![]() ,
то делаем вывод, что система имеет
множество решений.
,
то делаем вывод, что система имеет
множество решений.
Получим общее решение системы. Рассмотрим последнее уравнение системы уравнений
![]() .
.
Выразим из него х2 , придавая при этом неизвестным х3 и х4 произвольные значения х3 = С1, х4 = С2:
х2 = - 3 – 13С1 +5С2 .
Подставим в первое уравнение системы найденные значения неизвестных х2, х3, х4 и выразим из него х1:
х1 = 5С2 – 8С1 – 1.
Таким образом, общее решение системы уравнений будет иметь вид
х1 = 5С2 – 8С1 – 1,
х2 = - 3 – 13С1 +5С2,
х3 = С1,
х4 = С2.
Из общего решения легко можно получить частное решение. Если положить, например, х3 = 0, х4 = 0, то х1 и х2 будут соответственно равны -1 и -3. Частное решение системы можно представить в виде совокупности четырех чисел (-1, -3, 0, 0).
Ответ.
 ,
где С1
и С2
– любые числа.
,
где С1
и С2
– любые числа.
Пример 5. Решить методом Гаусса систему
![]() .
.
Решение. Составим расширенную матрицу системы и обнулим с помощью элементарных преобразований элементы, стоящие под главной диагональю:
![]() ~
~
![]()
Ранг расширенной матрицы системы равен двум
![]() ,
,
т.к. данная матрица содержит наивысший минор второго порядка, отличный от нуля
![]() .
.
Ранг
основной матрицы системы
![]() равен одному
равен одному
![]() ,
,
т.к.
отличный от нуля минор имеет первый
порядок
![]() .
Поскольку ранги основной и расширенной
матриц системы не равны между собой
.
Поскольку ранги основной и расширенной
матриц системы не равны между собой
![]() ,
,
то данная система линейных алгебраических уравнений решений не имеет.
Ответ. Решений нет.
