54. Статистичний розподіл вибірки двомірної випадкової величини та числові характеристики її складових.

У ході статистичного дослідження системи двох випадкових величин Х і У, як і в одновимірному випадку, спершу будується емпіричний закон сумісного розподілу. Для цього формується вибірка певного обсягу n, елементами якої є відповідні пари чисел (x_і , у_і). Таку вибірку записують у формі таблиць.

Числові характеристики для не згрупованої вибірки

М^*(Х) = х_в= , М^*(Y) = y_в= ;

D^*(Х) = D_вx= , D^*(Y) = D_вy= .

Для згрупованої вибірки:

М^*(Х) = х_в= , М^*(Y) = y_в= ,

D^*(Х) = D_вx= , D^*(Y) = D_вy= ,

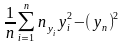52. Перевірка гіпотез про вигляд математичного сподівання нормально розподіленої випадкової величини у випадку коли дисперсія відома.

Коли дисперсія генеральної сукупності Д_r(Х) відома. Допускається, що відомі п,а₁,а.

Правило 1. Якщо Н₀:а = а₀, а Н₁ : а а₀, то перевірка гіпотези здійснюється за правилом:

1. Обчислюється х_в.

2. Обчислюється емпіричне значення критерію за формулою

3.За таблицею значень інтегральної функції Лапласа знаходять критичну точку k_kp двосторонньої критичної області з рівності

3. Робиться висновок :

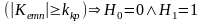
Правило 2. Якщо Н₀:а = а₀, а H₁ : а > а₀, то перевірка гіпотези здійснюється подібно до правила 1 із змінами:

1. Визначають критичну точку k_п.кр правосторонньої критичної області, користуючись при цьому) рівністю

2. Робиться висновок:

Правило 3. Якщо Н₀:а = а₀, а II, \ а < а₀, то перевірка гіпотези здійснюється подібно до попереднього правила 2 із змінами у висновку, ураховуючи, що критична точка лівостороння, тобто що к_{л кр} - -к_пІкр :

50. Критерій узгодження Пірсона ( критерій )для перевірки гіпотези про закон розподілу генеральної сукупності.

Критерії, які призначені для перевірки сформульованих гіпотез, називаються критеріями узгодження. Згідно з критерієм Пірсона для перевірки гіпотези вводиться випадкова величина К:

,

Де m- число варіант(чи інтервалів);

- спостережувана частота

- теоретична частота

- імовірність того, що значення випадкової величини Х належить до і-тої групи.