41. Умовні закони розподілу системи двох дискретних випадкових величин та їх числові характеристики.

Умовним законом розподілу ДВВ Х за фіксованого значення Y= називається перелік усіх можливих значень величини Ч та відповідних їм умовних імовірностей

Математичні сподівання:

Умовні дисперсії

Умовні середні квадратичні відхилення

42. Статистичний розподіл вибірки та його числові характеристики.

Дискретним статистичним розподілом вибірки називається перелік витрат і відповідних їм частот чи відносних частот Інтервальним статистичним розподілом вибірки називають відповідність між інтервалами варіаційного ряду та накопиченими частотами чи відносними накопиченими частотами. Числові характеристики: Вибірковим середнім статистичного розподілу вибірки називається середнє арифметичне значення її варіант з урахуванням їх частот .

Розмах вибірки – це різниця між найбільшим і найменшим значеннями іі варіантами.

Вибіркова дисперсія (або статистичного розподілу вибірки – це вибіркова середня квадратів різниць між варіантами та їх вибірковими середніми або Вибіркове середнє квадратичне відхилення: Мода дискретного статистичного розподілу вибірки називається те значення варіанти , якому відповідає найбільша частота . Медіаною дискретного статистичного розподілу вибірки називається значення середнього елемента варіаційного ряду.

43. Емпірична функція розподілу.

Емпіричною функцією розподілу випадкової величини Х називається функція , яка визначає для кожного значення x відносну частоту події Х<x, тобто , де - накопичена частота для тих значень випадкової величини Х, що менші за деяке дійсне число x,n- обсяг вибірки.

Основні властивості емпіричної функції розподілу

1. 0

2. Функція неспадна

3. для х

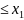
4. =1, для x>

45. Точкова оцінка математичного сподівання нормально розподіленої випадкової величини.

За точкову оцінку М* математичного сподівання а=М(Х) генеральної сукупності вибирають вибіркове середнє тобто Статистична оцінка невідомого параметра генеральної сукупності одним числом називається точковою. Точковою оцінкою невідомого параметра Θ генеральної сукупності називають однозначно визначену функцію Θ* = Θ*(х1, х2,...хп) на основі вибірки, за допомогою якої знаходять наближене значення параметра Θ.За точкову оцінку М* математичного сподівання а=М* генеральної сукупності вибирають вибіркове середнє, тобто М^*= х_в = n_ix_i

44. Поняття точкової оцінки параметра розподілу випадкової величини та її незміщеність, змістовність і ефективність. Зв'язок точкових оцінок параметрів розподілу випадкової величини з її числовими характеристиками. Точкова оцінка параметра – це статистична оцінка невідомого параметра генеральної сукупності одним числом.

1)Оцінка параметра називається незміщеною, якщо за будь-якого обсягу вибірки її математичне сподівання дорівнює параметру, який оцінюється, тобто .В іншому випадку оцінка називається незміщеною.

2)Оцінка параметра 𝛩 називається ефективною, якщо вона має найменшу дисперсію серед усіх оцінок, які обчислені за вибірками одного і того ж обсягу n.

3) при розгляді великих за обсягом вибірок додається ще вимога змістовності. Оцінку 𝛩* називається змістовною, якщо при n→∞ вона прямує за ймовірністю до оцінюваного параметра 𝛩, тоюто виконується рівність

Якщо при n→∞ дисперсія незміщеної точкової оцінки прямує до нуля, то така оцінка є також змістовною. За точкову оцінку M* математичного сподівання a=M(X) генеральної сукупності вибирають вибіркове середнє. За точкову оцінку D* дисперсії D(X) генеральної сукупності вибирають зміщену точкову оцінку дисперсії або незміщену вибіркову дисперсію. Точкова оцінка * середнього квадратичного відхилення обчислюється як середнє квадратичне відхилення

46. Точкова оцінка дисперсії і середнього квадратичного відхилення нормально розподіленої випадкової величини. За точкову оцінку Д* дисперсії Д(Х) генеральної сукупності вибирають зміщену точкову оцінку дисперсії

D^* = D_в = n_i(x_i – x_в)² = n_i x_i² - x_в² або незміщену (виправлену) вибіркову дисперсію D^* = D_в = D_{в =} Точкова оцінка σ* середнього квадратичного відхилення σ(Х) генеральної сукупності обчислюється за формулою ^{σ * =}