28. Дисперсія і середнє квадратичне відхилення неперервної випадкової величини.

Дисперсією неперервної випадкової величини Х називають математичне сподівання квадрата її відхилення Х – М(Х), тобто :

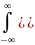D(X) = якщо можливі значення величини Х зосереджені на інтервалі (а; b) , і D(X) = якщо можливі значення величини Х містяться на всій осі Ox .

Для обчислення дисперсії неперервної випадкової величини часто використовують більш зручні формули : D(X) = D(X) =

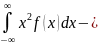
Середнє квадратичне відхилення σ(Х) неперервної випадкової величини Х визначається рівністю : σ(Х) = Дисперсія і середнє квадратичне відхилення неперервної випадкової величини характеризують « розсіювання » можливих її значень в околі точки осі Ох, яка зображає математичне сподівання.

30. Числові характеристики рівномірно розподіленої випадкової величини.

Математичне сподівання М(Х) =

Дисперсія D(X) =

Середнє квадратичне відхилення σ(Х) =

31. Нормальний закон розподілу ймовірностей неперервної випадкової величини та ймовірностей зміни параметрів розподілу.

НВВ Х називається розподіленою за нормальним законом (або нормально-розподіленою) з параметрами -∞<а<∞ і Ϭ>0, якщо густина розподілу ймовірностей має вигляд

32. Формула для обчислення імовірності попадання значень нормально розподіленої випадкової величини в заданий інтервал.

, де a, b – межі інтервалу.

29. Рівномірний закон розподілу ймовірностей випадкової величини та графіки її густини й функції розподілу.

НВВ Х називається рівномірно розподіленою на проміжку [a;b] , якщо її густина f (x) на цьому проміжку є сталою величиною С.

Стала С не є довільною. Оскільки , то С = f(x) = F(x)=

34. Числові характеристики показниково розподіленої випадкової величини.

Математичне сподівання Середнє квадратичне відхилення Ϭ(X)= Дисперсія D(X)=

35. Формула для обчислення ймовірності попадання значень показникові розподіленої випадкової величини в заданий інтервал.

Імовірність того, що показникові розподілена випадкова величина Ч набуде значень з проміжку (x1;x2) –

36. Теорема Чебишева та стійкість середнього арифметичного випадкових величин.

Теорема Чебишева: Нехай Х1, Х2, …, Хn- попарно незалежні випадкові величини, які мають скінченні математичні сподівання та обмежені в сукупності дисперсії (обмежені одним і тим самим числом С, тобто для усіх i=1,2,…,n, і нехай ( у позначеннях) , . Тоді тобто практично з достовірністю можна стверджувати, що різниця між середнім арифметичним випадкових величин і середнім арифметичним їх математичнх сподівань є як завгодно малою, якщо n – число випадкових величин є досить великим. Середнє арифметичне великого числа незалежних випадкових величин втрачає випадковий характер і має властивість стійкості.

33. Показниковий розподіл імовірностей неперервної випадкової величини.Графік густини й функції розподілу.

НВВ Х називається розподіленою за показниковим законом з параметром λ, якщо густина розподілу її ймовірностей має вигляд формули

Графік густини:f(x)λ

• x

Графік функції розподілу:

F(x)

1 ………………………………..

O x

37. Теорема Бернуллі і стійкість відносних частот.

Якщо в кожному з n незалежних повторних випробуваннях імовірність появи події A є однаковою і дорівнює p, то за досить великого n має місце рівність 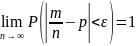, де відносна частота появи події А, m – число появ події A, n – число випробувань, - будь-яке як завгодно мале число. Теорема Бернуллі стверджує, що відносна частота події А за досить великого числа випробувань є стійкою величиною.

38. Центральна гранична теорема і її граничне значення.

Теорема: Нехай випадкові величини Х1, Х2,…Хn, - незалежні і однаково розподілені, причому ? , i=1,2,…n. Розглянемо випадкову величину , для якої Тоді закон розподілу суми за наближається до нормального з математичним сподіванням і середнім квадратичним відхиленням 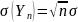, тобто

39. Система двох випадкових величин, її закон розподілу та числові характеристики складових.

Розгляд двох чи більше випадкових величин в їх взаємозалежності розуміється як система випадкових величин. Така система ще має назву багатовимірної випадкової величини.

Законом розподілу ймовірностей ДДВВ (X,Y) називається перелік її можливих значень ( та відповідних ймовірностей p( спільної їх появи.

Числові характеристики її складових знаходяться як для одновимірної ДВВ.

40. Кореляційний момент і коефіцієнт кореляції.

Кореляційний момент випадкових величин (X,Y) називається математичне сподівання добутку відхилен цих величин, тобто

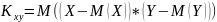
Для обчислення кореляційного моменту ДДВВ користуються формулою або .

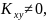Якщо випадкові величини X I Y – незалежні то , якщо ж то величини X I Y є залежними.

Коефіцієнт кореляції це величина яка характеризує лише ступінь лінійної залежності між випадковими величинами X I Y.