8. Елементарні функції та їх класифікація.

Елементарні функції — клас функцій, що містить в собі степеневі функції, многочлени, показникові функції, логарифмічні функції, тригонометричні функції, зворотні тригонометричні функції, а також функції, що отримуються із перелічених вище за допомогою чотирьох арифметичних операцій (додавання, віднімання, множення, ділення) та композиції, застосованих скінченну кількість разів. Наприклад, раціональні функції є відношеннями многочленів, тому вони належать до елементарних функцій. Так само, неважко переконатися, що до елементарних функцій належать гіперболічні та зворотні гіперболічні функції.

Елементарні функції поділяються на алгебраїчні і трансцендентні.

9. Основні елементарні функції. Їх властивості, графіки.

Основні елементарні функції;

1.Степенева

2.Показникова

3.Логарифмічна

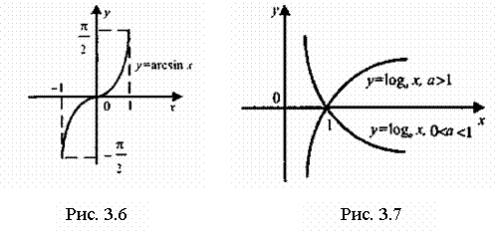
4.Тригонометрична

5.Обернені тригонометричні

10. Границя функції при х прямує до нескінченності.

Нехай функція f(x) визначена при хх₀ (хх₀).

Визначення 5. Число А називається границею функції f(x) при х (х-), якщо для будь-якого можна знайти таке , що при всіх х, які задовольняють нерівності , виконують нерівність

При цьому вживають відповідні позначення

f(x)=A f(x)=A

або

f(x)A, х+ (f(x)A, х-).

В разі, якщо існують границі функції f(x) як при х+, так і при х-, причому f(x)= f(x)=A , то вживають позначення

f(x)=A або f(x)A, х

Вище малося на увазі, що А – певне число. Іноді зручно розглядати нескінченні границі функції.

11. Означення границя функції на мові "ε-δ". Геометричний зміст границі.

12. Означення границі функції на мові "послідовностей".

13. Поняття нескінченно малої величини і її властивості.

1. 

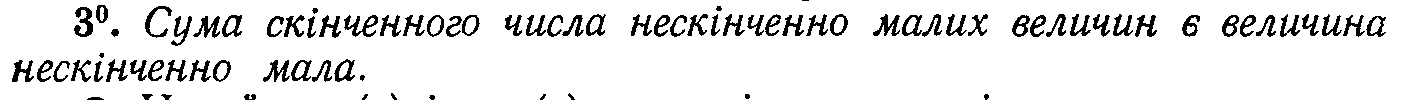
14. Поняття нескінченно великої величини і її властивості.

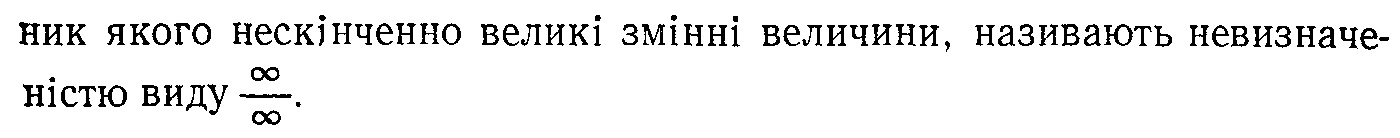
15. Порівняння нескінченно малих функцій.

Аналітична геометрія - розділ математики, в якому властивості геометричних об’єктів вивчаються засобами алгебри на основі методу координат. Основоположником аналітичної геометрії вважають Декарта,який вперше в 1637 році у своїй книзі «Геометрія» дав чіткий виклад ідеї методу координат на площині. Декарт запропонував положення точки на площині відносно заданої системи координат визначати за допомогою 2 чисел - її координат, а кожну лінію на площині розглядати як множину точок,заданих певною геометричною умовою. Ця умова записується у вигляді рівняння,що зв’язує змінні координати точок,що належать даній лінії назив. рівнянням цієї лінії. Такий спосіб дослідження геометричних об’єктів і називається методом координат.

Положення точки на прямій визначається числом, що називається координатою цієї точки. Приклад : точка А має координату -1,5, точка В - координату 3. Пишуть: А(-1,5), В(3).

16. Теорема про границю суми, добутку і частки.

17.

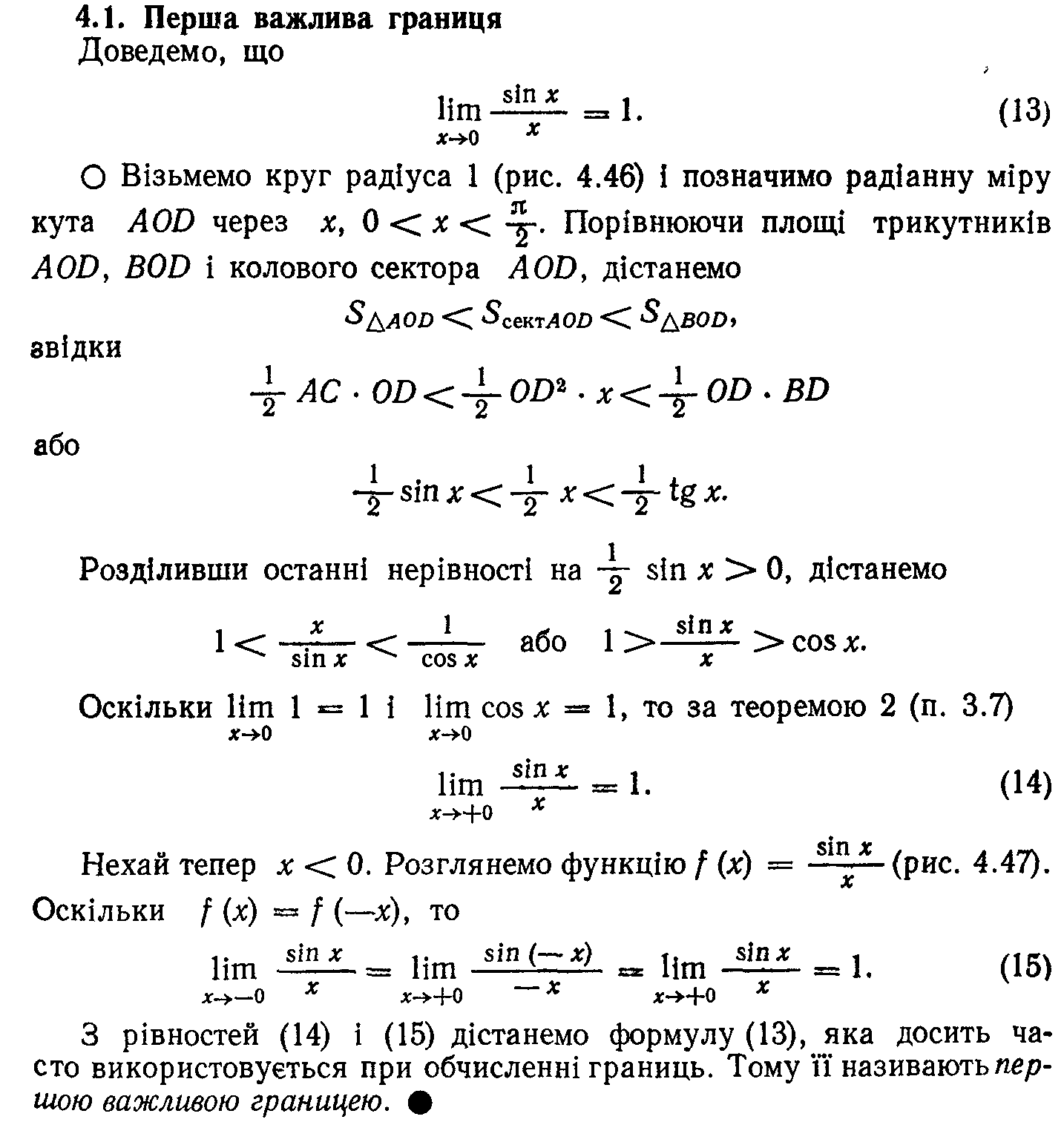
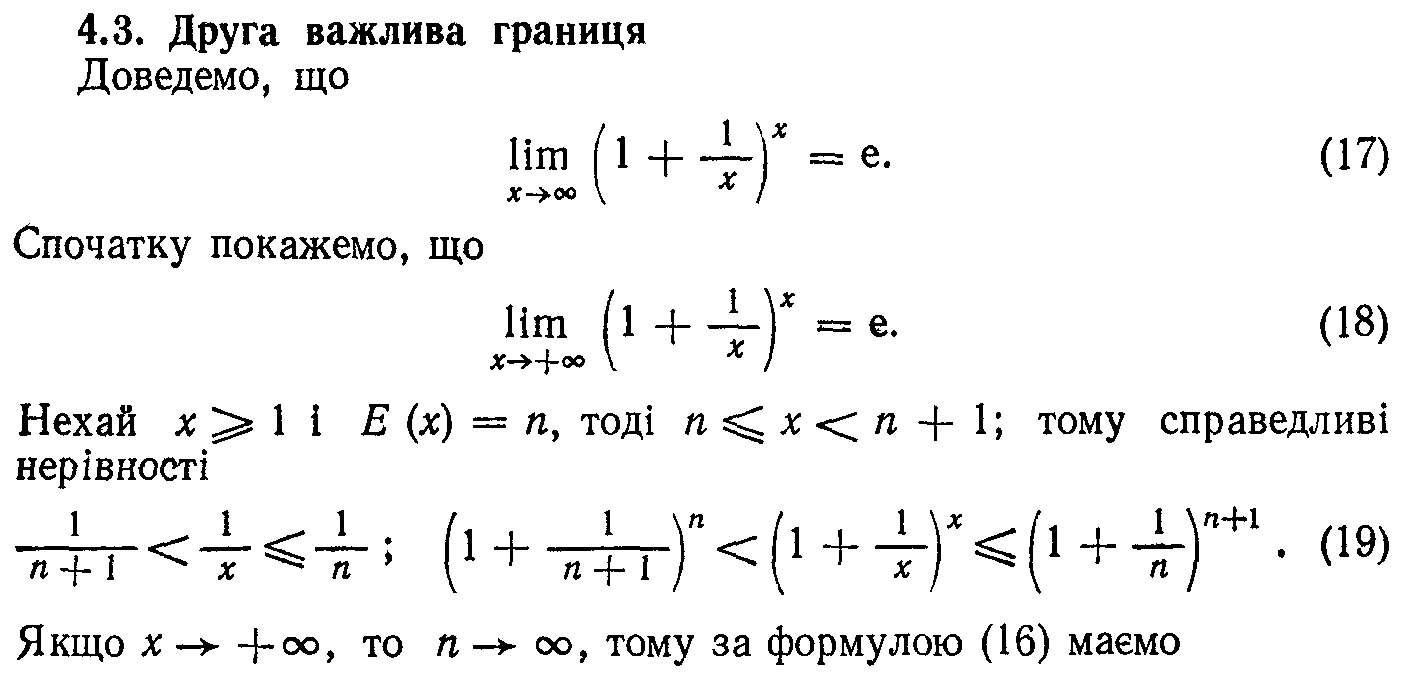
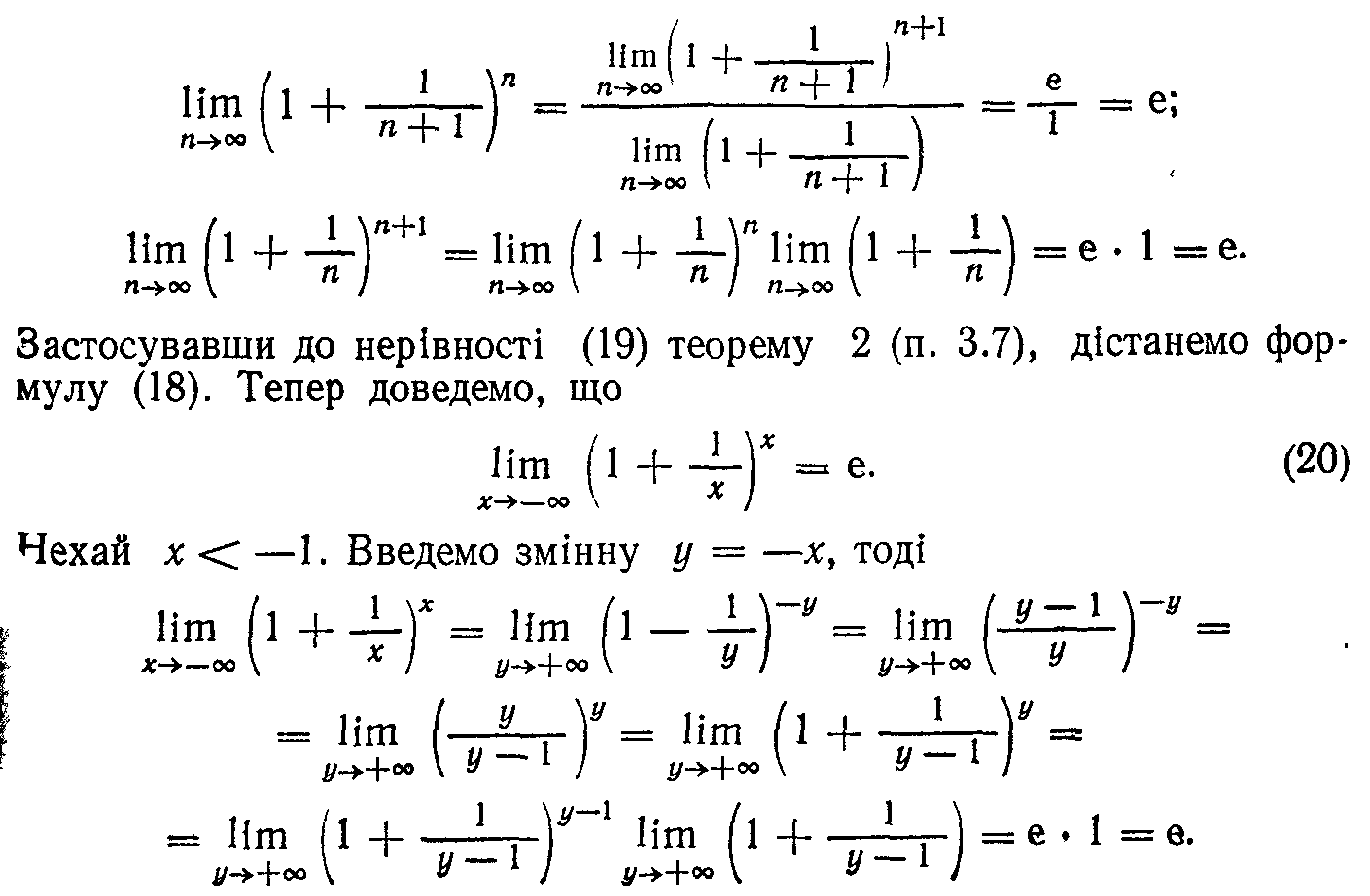
18. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.

19. Означення неперервної функції на інтервалі і на відрізку. Теорема Больцано-Коші (перша, друга). Теорема Вейерштрасса.

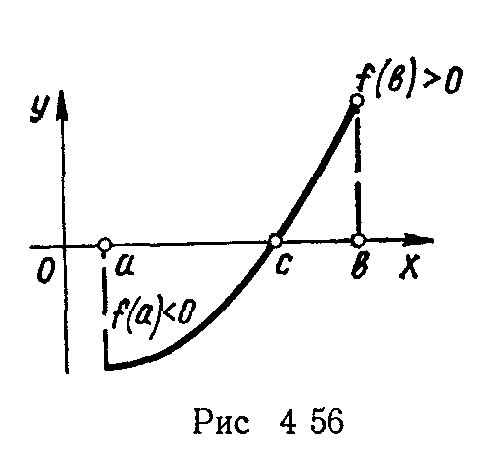
20. Точки розриву І та II роду

21. Означення похідної функції в точці. Геометр зміст похідної

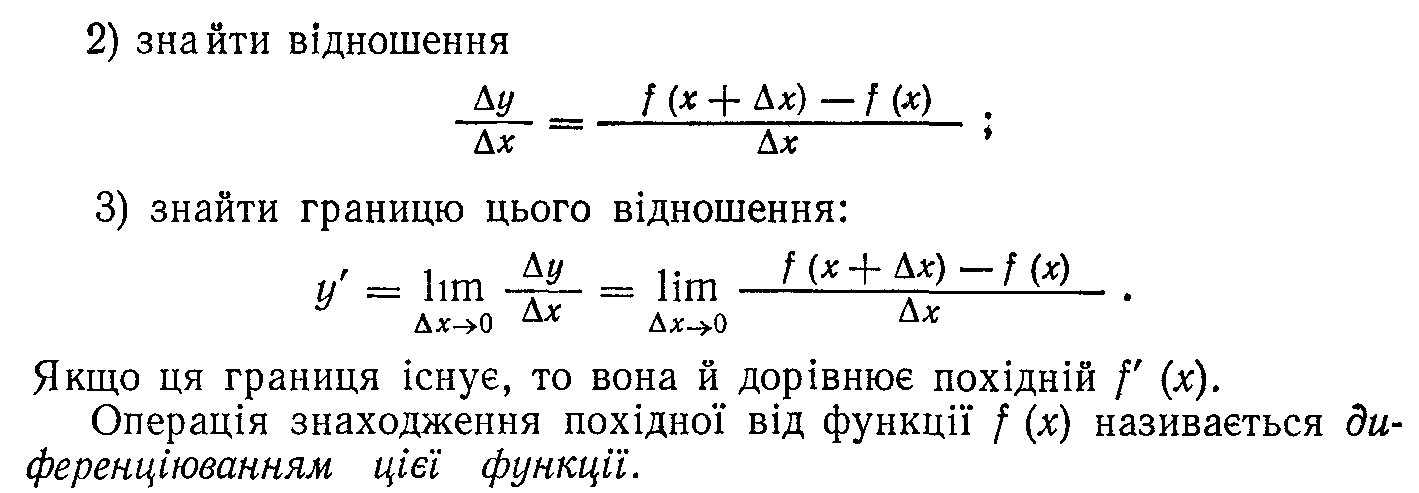
22. Поняття диференційованості функції в точці і на проміжку. Теорема про диференційованість і неперервність функції в точці

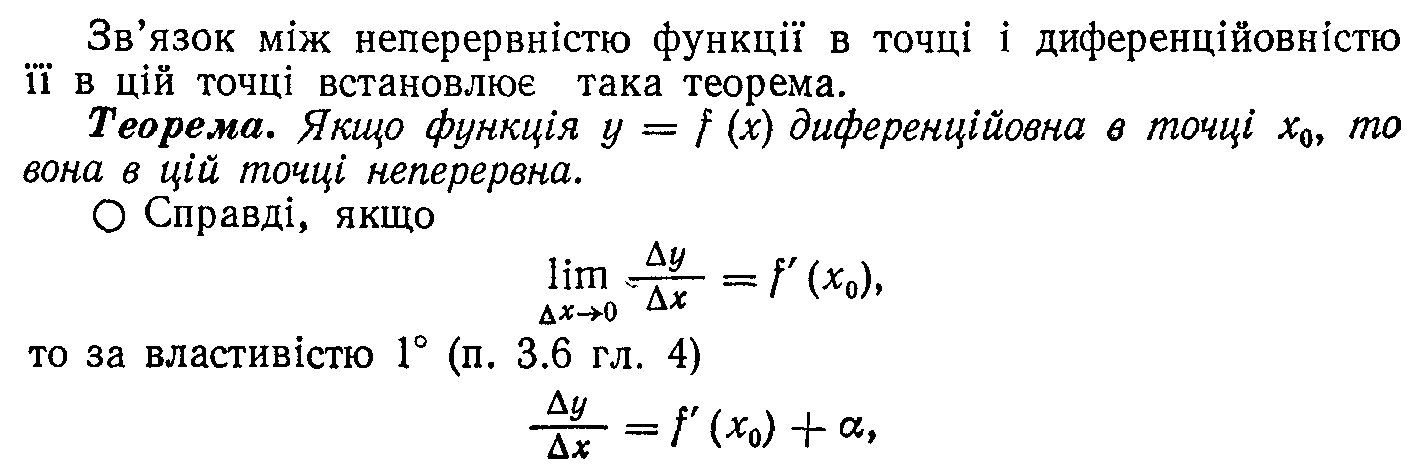
23. Правила диференціювання суми, різниці, добутку і частки. Таблиця похідних

2 4. Складена функція та її похідна

Функцію g(x) називають внутрішньою функцією, або проміжною змінною, функцію f(u) — зовнішньою функцією. Отже, щоб обчислити значення складеної функції у = f(g(x)) в довільній точці х, спочатку обчислюють значення й внутрішньої функції g, а потім f(u).

Приклад 2. Розглянемо функцію у = . Вона є складеною із функцій u = cos х,

у = , де cos х – внутрішня функція, — зовнішня функція.

25. Похідні вищих порядків

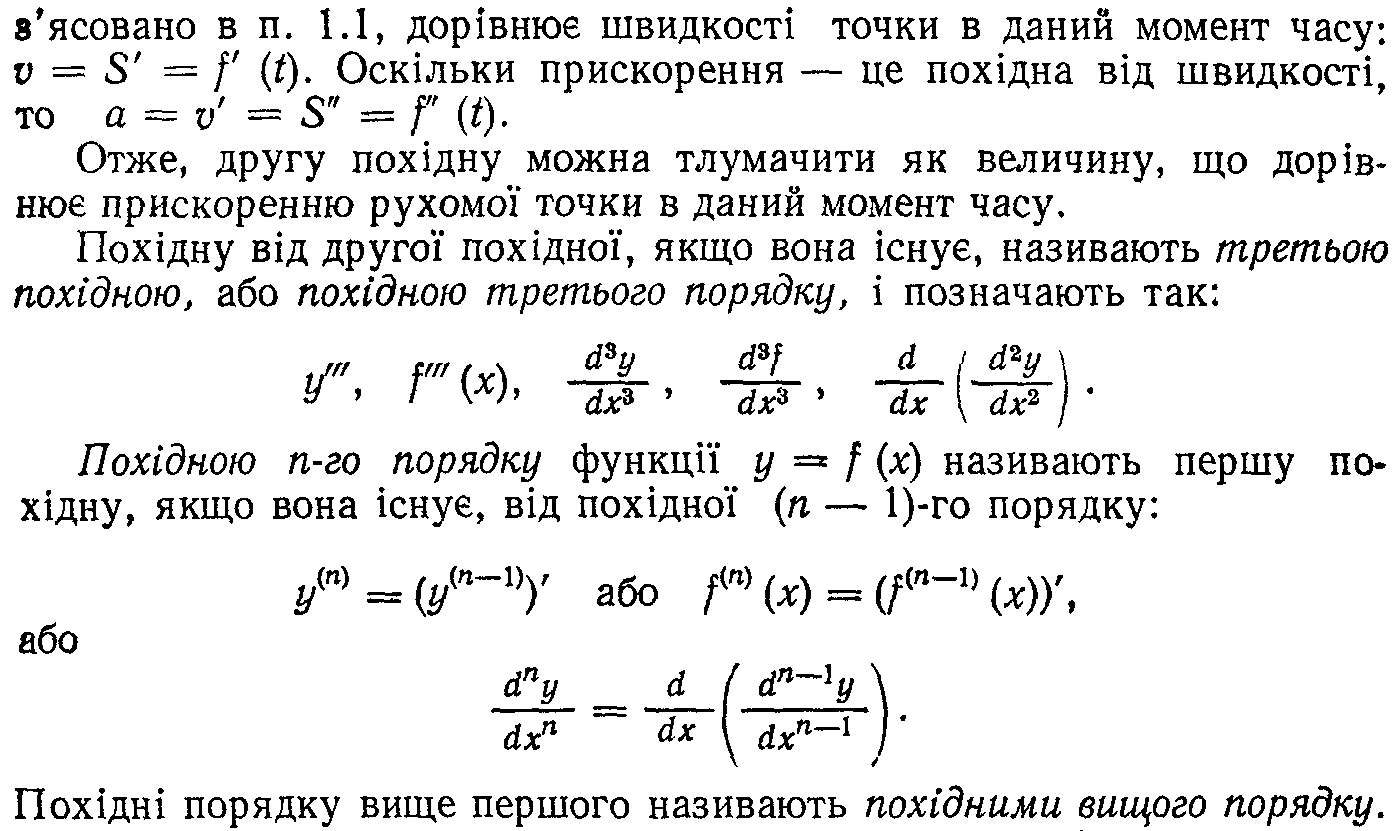
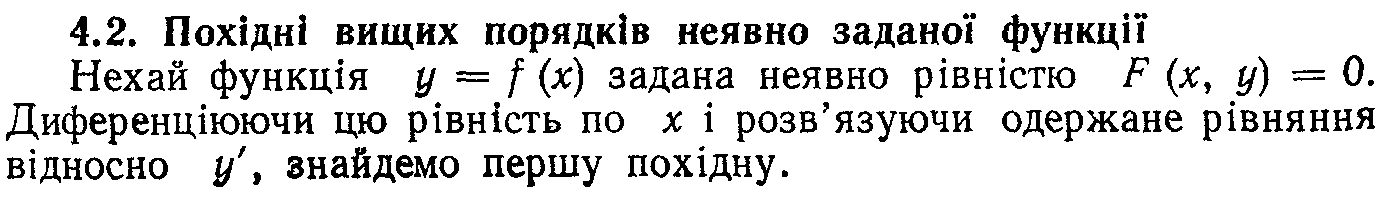
26. Поняття диференціала. Геометричний зміст

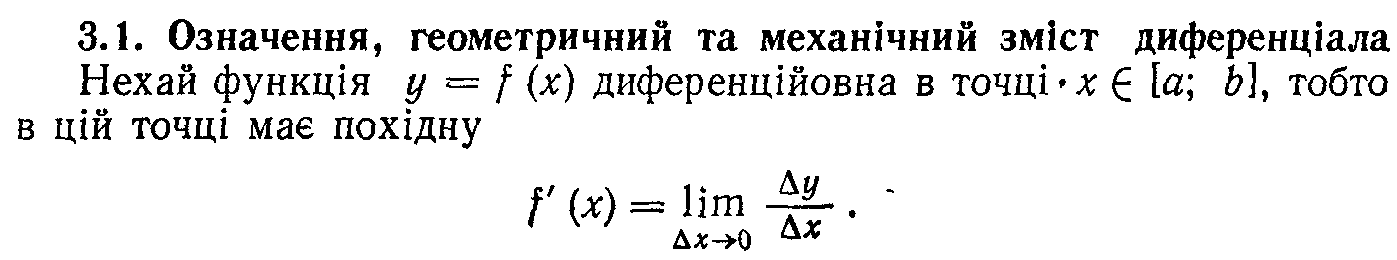
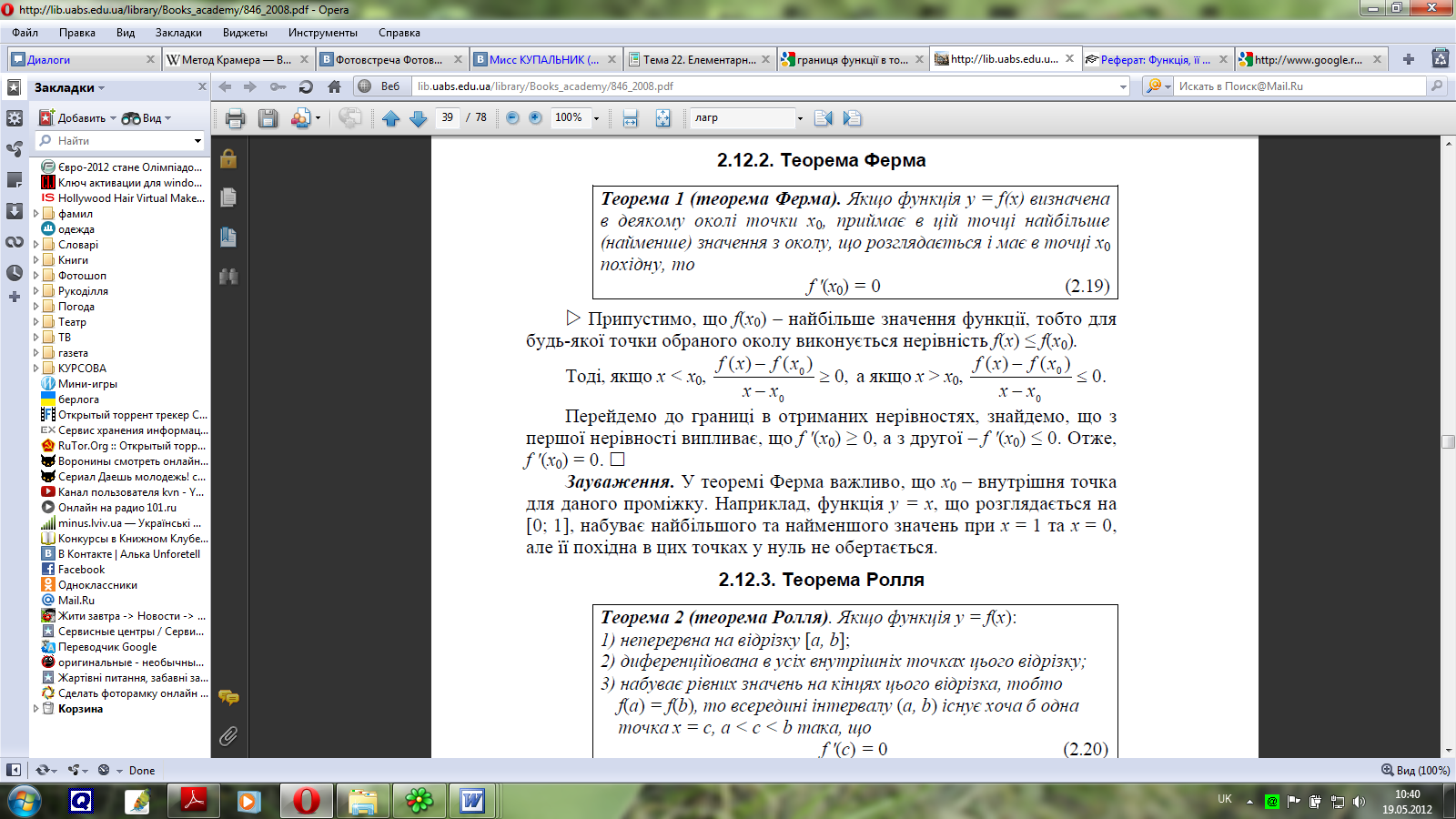
27. Основні теореми диференціального числення

28. Правило Лопіталя

29. Зростаюча та спадна функції. Монотонна функція. Необхідна і достатня умова зростання і спадання функції

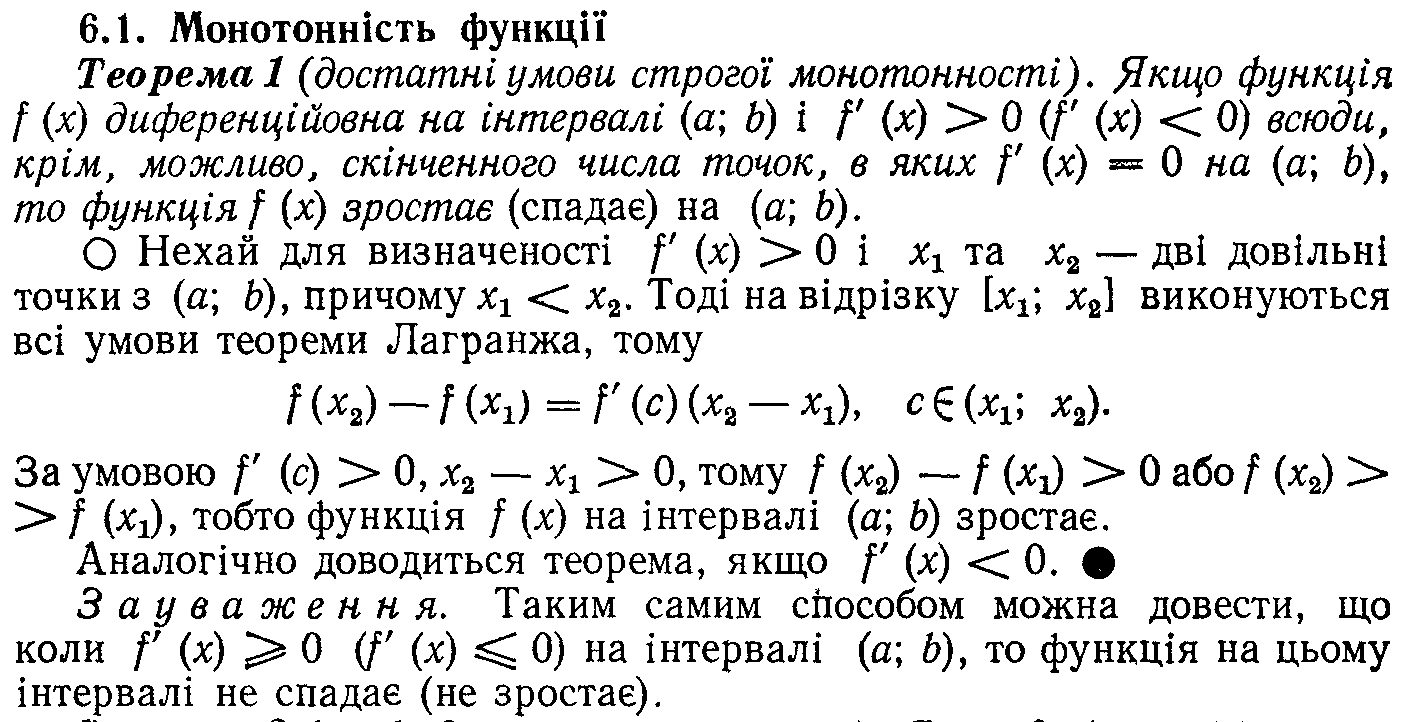
30. Екстремум функції в точці. Необхідна і достатня умова екстремуму. Найбільше та найменше значення функції на відрізку.

Точка х0 називається точкою локального максимуму (або мінімуму) функції f(х), якщо існує такий окіл 0 <| х — х₀ |< б точки x0, який належить області визначення функції, і для всіх х з цього околу ви­конується нерівність f(х) < f(х₀)/

Точки локального максимуму і локального мінімуму називаються точками локального екстремуму, а значення функції в цих точках називаються відповідно локальним максимумом і локальним мінімумом або локальним екстремумом. Не слід плутати локальний максимум з найбільшим зна­ченням функції якого вона може набувати в області ви­значення (його називають також абсолютним максимумом). Локаль­них максимумів функція може мати кілька, абсолютний максимум може бути тільки один.

Теорема 1 (необхідна умова локального екстремуму). Якщо функ­ція f(х) має в точці х₀ локальний екстремум і диференційована в цій точці, то f'(х₀) = 0.

Теорема 2 (перша достатня умова локального екстремуму): якщо при переході зліва направо через критичну точку х₀ знак похідної f'(х) змінюється з плюса на мінус, то х₀ — точка локального максимуму; якщо знак похідної f' (х) змі­нюється з мінуса на плюс, то х₀ — точка локального мінімуму; якщо похідна не змінює знак, то в точці х₀ екстремум відсутній.

Теорема 3 (друга достатня умова локального екстремуму). Нехай х₀— стаціонарна точка функції f(х), тобто f' (х₀) =0, і в околі точки х₀ існує друга неперервна похідна, причому f" (х₀)не дорівнює 0. Якщо f" (х₀) > 0, то х0— точка локального мінімуму; якщо f (х₀) <;0, то х₀ — точка локального максимуму.

Найбільшим значенням функції на відрізку називається найбільше з усіх її значень на цьому відрізку, а найменшим - найменше з усіх її значень.