Задание № 1. Задача линейного программирования

Предприятие выпускает два вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида а₁ , а₂ , а₃ кг соответственно, а для единицы изделия В – b_{1 ,} b_{2 ,} b₃ . Производство обеспечено сырьем каждого вида в количестве P_1, P_2, P₃ . Стоимость единицы изделия А составляет α руб., а единицы изделия В – β руб. Требуется составить план производства изделий А и В, обеспечивающий максимальную стоимость готовой продукции.

а) Составить экономико-математическую модель задачи,

б) Решите задачу симплекс-методом,

в) Сформулируйте двойственную задачу и найдите ее решение,

г) Решите исходную задачу графически.

Задание № 1

№ Варианта	а1	а2	а3	b1	b2	b3	P1	P2	P3	α	β
2	4	2	1	1	3	5	240	180	251	40	30

Решение.

а) Экономико-математическая модель.

Обозначим x₁ – количество изготовленных единиц изделия А, x₂ – количество изготовленных единиц изделия В.

Целевая функция, которую нужно максимизировать – стоимость готовой продукции:

.

Возможное количество продукции ограничено количеством сырья трех видов. Система ограничений:

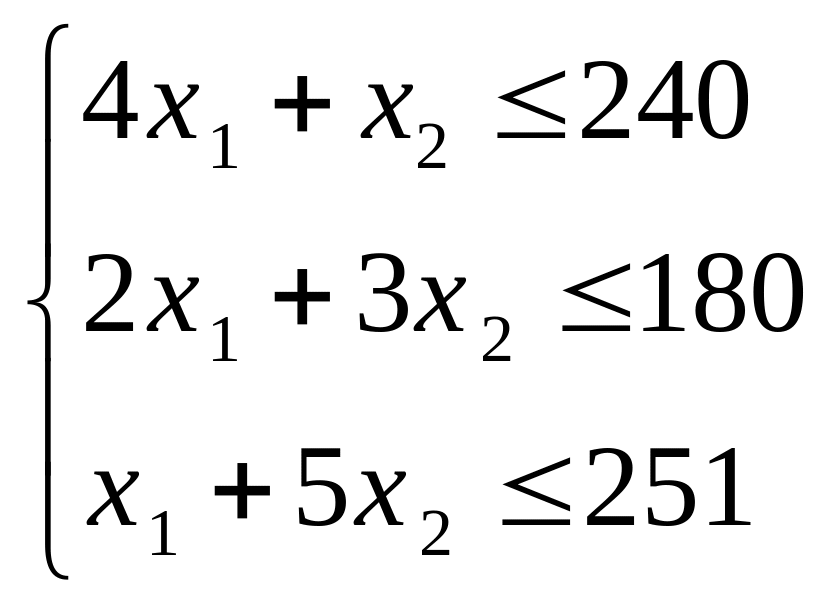
Условия неотрицательности переменных:

.

Получили задачу линейного программирования.

б) Решение симплекс-методом.

Перейдем к каноническому виду ЗЛП. Введём балансовые переменные .

, .

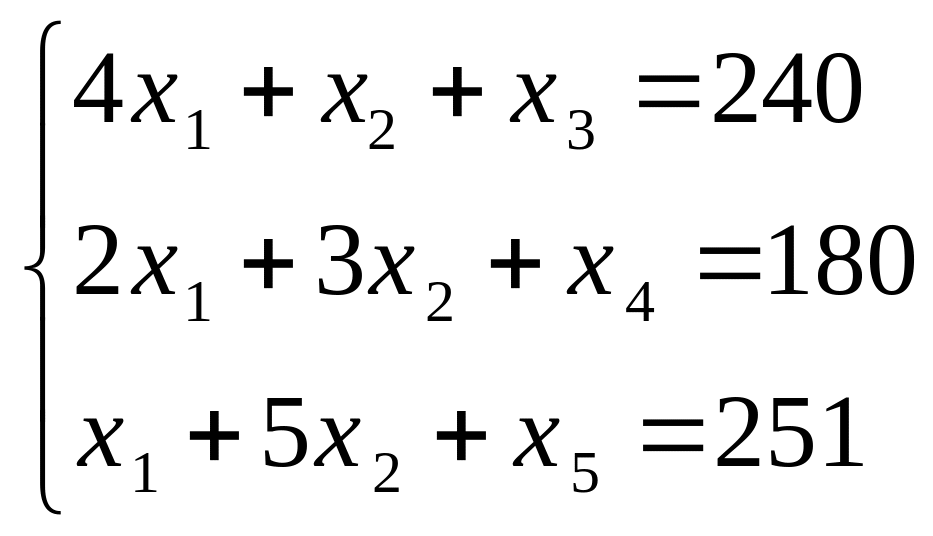Базисные переменные ; свободные переменные .

Если , то .

Получили базисный допустимый план .

1-я симплекс-таблица.

	j	1	2	3	4	5	6
i	базис	x1	x2	x3	x4	x5	свобод. члены bi	симплекс-отношения
1	x3	4	1	1	0	0	240	240/4=60=min
2	x4	2	3	0	1	0	180	180/2=90
3	x5	1	5	0	0	1	251	251/1=251
4		-40	-30	0	0	0	0

План не оптимальный, так как в последней строке есть отрицательные оценки. Выберем разрешающий столбец 1, для которого отрицательная оценка наибольшая по абсолютной величине. Вычисляем отношения свободных членов к положительным элементам разрешающего столбца (симплекс-отношения). Разрешающая строка 1, для которой это отношение наименьшее. Разрешающий элемент .

Переменная входит в базис, выводится из базиса.

Переходим к новой таблице по правилам симплекс-метода.

2-я симплекс-таблица.

	j	1	2	3	4	5	6
i	базис	x1	x2	x3	x4	x5	свобод. члены bi	симплекс-отношения
1	x1	1	1/4	1/4	0	0	60	60/(1/4)=240
2	x4	0	5/2	-1/2	1	0	60	60/(5/2)=24
3	x5	0	19/4	-1/4	0	1	191	191/(19/4)=40,2
4		0	-20	10	0	0	2400

План не оптимальный, так как в последней строке есть отрицательная оценка. Разрешающий столбец 2, для которого оценка отрицательна. Разрешающая строка 2, для которой симплекс-отношение наименьшее. Разрешающий элемент .

Переменная входит в базис, выводится из базиса.

Переходим к новой таблице.

3-я симплекс-таблица.

	j	1	2	3	4	5	6
i	базис	x1	x2	x3	x4	x5	свобод. члены bi	симплекс-отношения
1	x1	1	0	3/10	-1/10	0	54
2	x2	0	1	-1/5	2/5	0	24
3	x5	0	0	7/10	-19/10	1	77
4		0	0	6	8	0	2880

Так как в последней строке нет отрицательных оценок, получили оптимальный план: , при котором .

Для получения максимальной стоимости готовой продукции нужно изготовить единицы продукции А и единицы продукции В. Стоимость продукции составит руб.

Значения балансовых переменных ; значит, сырье 1-го и 2-го вида будет израсходовано полностью, сырье 3-го вида останется неизрасходованным в количестве 77 кг.

в) Двойственная задача.

Из прямой задачи получаем двойственную задачу:

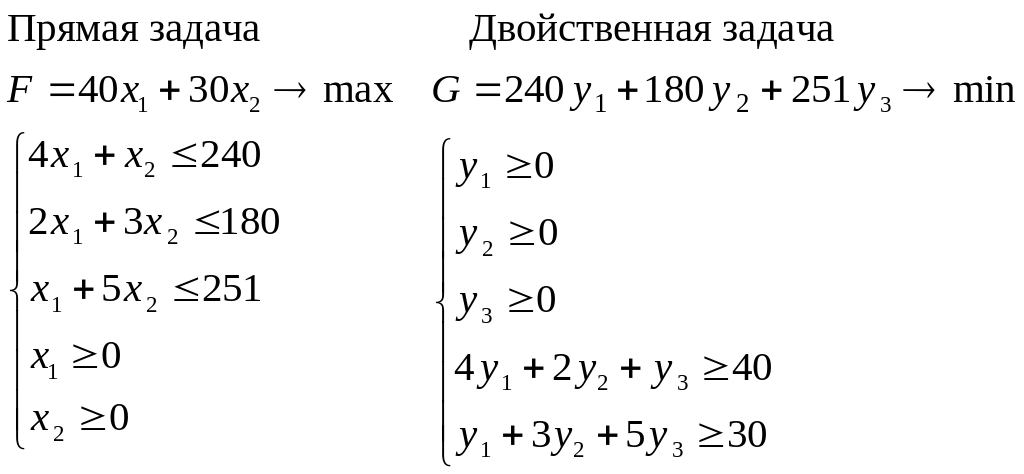
Зная оптимальное решение прямой задачи , находим решение двойственной задачи.

Подставим в систему неравенств прямой задачи:

По 2-й теореме двойственности, неравенства двойственной задачи, соответствующие строгим неравенствам прямой задачи, обращаются в равенства. Получаем систему

,

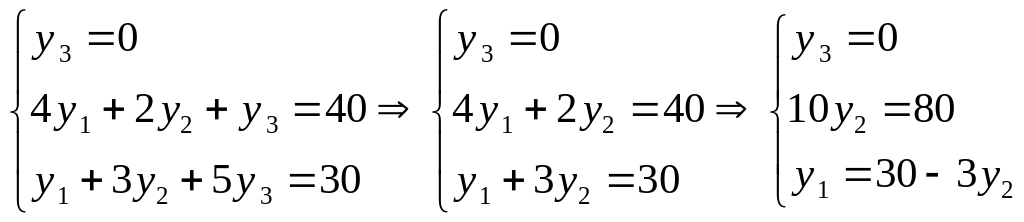откуда оптимальное решение двойственной задачи

.

Минимальное значение целевой функции .

В соответствии с 1-й теоремой двойственности, получили .

г) Графическое решение исходной задачи.

Строим область допустимых решений (ОДР).

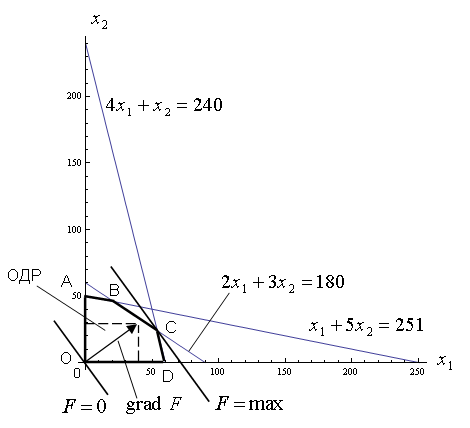
ОДР – выпуклый многоугольник ОABCD.

Вектор показывает направление возрастания функции F.

Линия соответствует значению функции при .

Перемещаем прямую параллельно самой себе в направлении вектора.

В своем крайнем положении в ОДР прямая проходит через точку С, значит, в этой точке целевая функция достигает максимума в ОДР.

Найдем координаты точки С.

Оптимальное решение , .

Максимальное значение целевой функции в ОДР

.

Решение, полученное графически, совпадает с решением, полученным симплекс-методом.