Алгебраический критерий устойчивости дискретной сау
Как
следует из раздела 4, непрерывная система
устойчива, если полюсы её передаточной
функции находятся в левой полуплоскости
комплексной переменной p.
Если, учитывая равенство
,
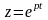представить передаточную функцию
дискретной системы в виде
,
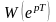то условие её устойчивости формулируется
аналогично: дискретная система устойчива,
если полюсы её передаточной функции
находятся в левой полуплоскости
комплексной переменной
.
При
замене переменных
левая полуплоскость переменной
преобразуется в круг единичного радиуса
на плоскости переменной
.
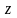Поэтому дискретная система устойчива,
если полюсы
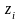её передаточной функции
находятся внутри окружности единичного
радиуса на плоскости переменной
и, следовательно, удовлетворяют условиям:
Представим
в виде:
.
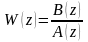Полюсы являются корнями характеристического уравнения системы:
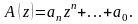
При
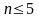удобно пользоваться алгебраическим
критерием устойчивости. В соответствии
с этим критерием дискретная система
устойчива, если коэффициенты её
характеристического уравнения
удовлетворяют определённой системе
неравенств.
Для уравнения первого порядка, т.е. при , эти неравенства записываются в виде:
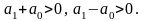
Для уравнения второго порядка ( ) они имеют следующий вид:
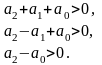
При указанная система неравенств принимает вид:
19 Частотный критерий устойчивости. Анализ детерминированных процессов в дискретных системах. Частотный критерий устойчивости дискретной сау
Замкнутая
дискретная система является устойчивой,
если годограф комплексного коэффициента
передачи разомкнутой системы не
охватывает точку
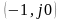на плоскости комплексной переменной
.
Так как комплексный коэффициент передачи
дискретной системы является периодической
функцией частоты, при построении
годографа достаточно изменять частоту
в пределах от
до
.
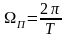9.5 Анализ детерминированных процессов в дискретных системах
Если начальные условия в системе нулевые, то
.
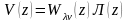Существует несколько способов нахождения процесса по его изображению . В общем случае этот переход определяется интегралом обращения (cм. свойства Z- преобразования). Для его вычисления можно использовать теорему о вычетах, в соответствии с которой:
,
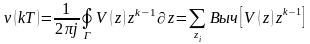где
-
полюсы подынтегральной функции
.
-
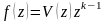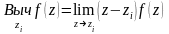вычет в случае простого полюса,
-
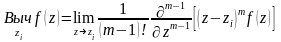вычет в полюсе
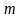-го
порядка.
Если достаточно знать значение выходного процесса только в установившемся режиме, то для определения его в устойчивой следящей системе по теореме о конечном значении оригинала:
.
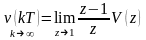20 Цифровые сау. Общая структура цифровой радиотехнической системы
Цифровыми называют следящие системы, все или часть блоков которых построены на базе цифровых вычислительных машин (ЦВМ) или в виде отдельных цифровых устройств, использующих элементы импульсной и цифровой техники. В противоположность им системы, не использующие цифровую технику, принято называть аналоговыми.
Достоинствами цифровых систем является резкое упрощение их настройки и регулировки, высокая стабильность их характеристик и параметров, высокая надёжность, удобство изменения их параметров в процессе работы, гарантированная точность получаемых результатов.
Основным недостатком, возникающим при построении цифровых систем, является то, что характерной особенностью этих систем является обработка процессов, подвергшихся дискретизации по времени и квантованию по уровню. В общем случае выполнение этих операций приводит к возрастанию ошибки слежения.