16 Передаточные функции дискретных систем. Пример дискретной системы

Использование Z-преобразования для анализа дискретных систем во многом аналогично использованию преобразования Лапласа при анализе непрерывных систем. Необходимым этапом такого анализа является нахождение передаточной функции дискретной системы, которая определяется как отношение Z-преобразований выходного и входного процессов системы при нулевых начальных условиях в системе. Познакомимся с методикой определения передаточной функции дискретной системы на примере системы, изображённой на рис. 9.2.

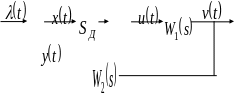
Рис.9.2. Пример дискретной системы

На рисунке приведены следующие обозначения:

- дискриминационная характеристика,

- импульсный элемент,

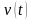- выходной процесс системы,

, - коэффициенты передачи звеньев.

На выходе импульсного элемента формируется напряжение:

При подаче его на вход фильтра с коэффициентом передачи на его выходе образуется процесс:

, где 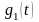- импульсная переходная функция фильтра.

По теореме свёртки и равенству имеем:

,

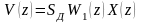где

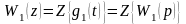- изображение импульсной переходной функции , совпадающей с Z- изображением передаточной функции , связанной с преобразованием Лапласа.

Ошибка слежения в рассматриваемой системе равна:

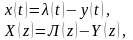
где

- Z-изображение процессов и ,

,

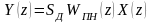где

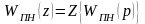- z- изображение функции 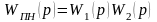, являющейся передаточной функцией приведённой непрерывной части системы.

Из формул и имеем:

.

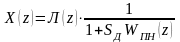Подставив это выражение в формулу для , получим:

.

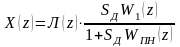Отсюда следует, что искомая передаточная функция рассматриваемой замкнутой дискретной системы описывается соотношением:

.

При анализе ошибок слежения в тактовых точках используется передаточная функция , связывающая z- изображения воздействия и ошибки слежения .

Так как , то

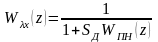
17 Разностные уравнения

Знание передаточной функции дискретной системы позволяет описать связь между дискретными процессами на её входе и выходе с помощью разностного уравнения. Чтобы получить это уравнение, представим передаточную функцию 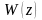системы в виде дробно-рациональной функции переменной :

.

Подставив это выражение в уравнение 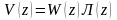, запишем:

.

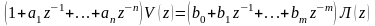Применим теорему обращения к обеим частям этого уравнения. Используя первую теорему смещения и полагая, что 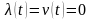при получаем:

,

где введены обозначения , .

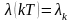Решив это уравнение относительно , представим его в виде:

.

Это выражение является разностным уравнением, связывающим значения выходного процесса с его значениями в предшествующих тактовых точках и значениями воздействия в моменты времени , , …, .

18 Коплексные коэффициенты передачи дискретной системы. Условия устойчивости дискретных сау

Если - передаточная функция и 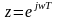, то .

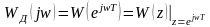Физический смысл комплексного коэффициента передачи дискретной системы заключается в следующем. На вход дискретной системы подаётся воздействие 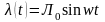. Возникающий при этом в установившемся режиме выходной процесс показан сплошной линией на рис.9.3. Как видно из рисунка выходной процесс является несинусоидальным, но в точках 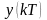совпадает со значениями непрерывного синусоидального процесса, имеющего частоту и комплексную амплитуду . Комплексный коэффициент передачи дискретной системы равен отношению комплексной амплитуды к комплексной амплитуде входного воздействия.

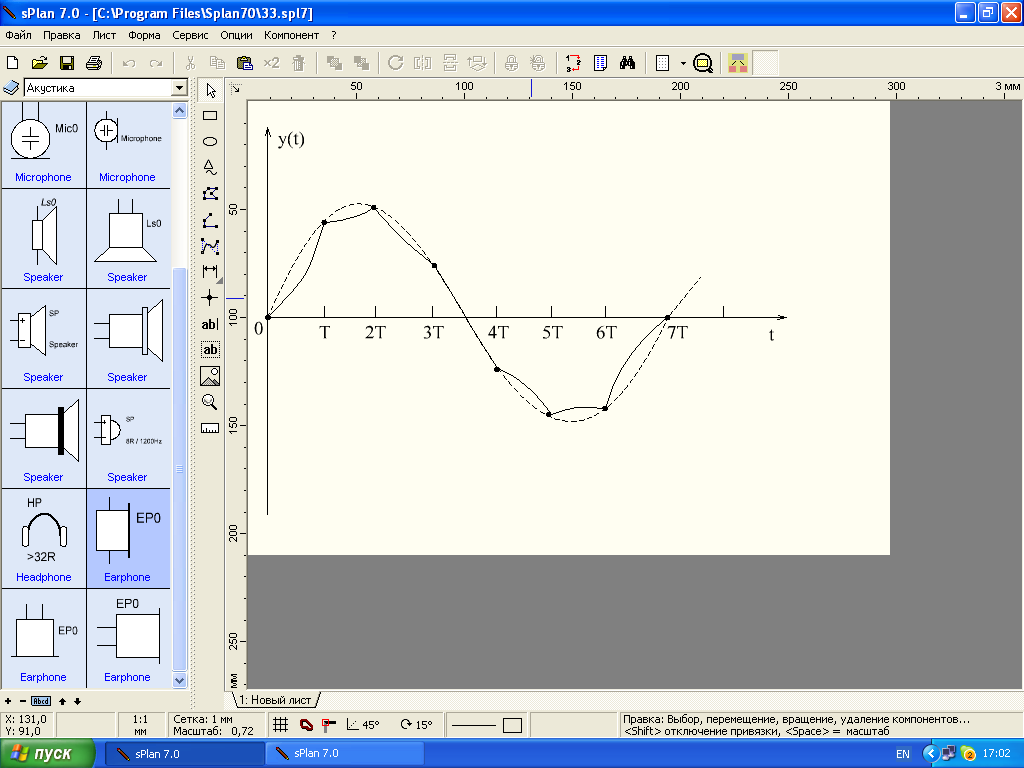
Рис.9.3. К понятию комплексного коэффициента передачи дискретной системы