8 Общий подход к методам анализа нелинейных систем автоматики

Работа в нелинейном режиме может быть вызвана выходом ошибки слежения за пределы линейного участка характеристики дискриминатора, наличием в системе ограничителей и других нелинейных элементов.

При больших отклонениях сигналов от установившихся значений приходится учитывать нелинейные свойства элементов систем радиоавтоматики, допускающих линеаризацию.

При составлении дифференциальных уравнений нелинейных систем радиоавтоматики сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы радиоавтоматики, а устройства, которые не могут быть линеаризированы, составляют нелинейную часть.

Во многих системах радиоавтоматики нелинейные устройства можно представить как статические, зависимость выходного сигнала от входного в которых описывается линейной зависимостью вида .

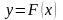Встречаются случаи, когда линейные устройства описываются дифференциальными уравнениями вида

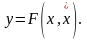
Характерной особенностью нелинейных систем является возможность возникновения в них автоколебаний.

Рассмотрим основные методы анализа нелинейных систем автоматики:

1. метод фазовой плоскости;

2. метод кусочно-линейной аппроксимации;

3. метод гармонической линеаризации;

4. метод статистической линеаризации;

5. метод моделирования.

9 Метод фазовой плоскости. Метод кусочно-линейной аппроксимации Метод фазовой плоскости

В ряде случаев поведение следящей системы описывается нелинейным дифференциальным уравнением 2-го порядка:

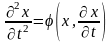(8.1)

Обозначив , уравнение (8.1) можно заменить системой уравнений 1-го порядка:

(8.2)

Cостояние системы, описываемой уравнениями (8.2), определяется в каждый момент времени величиной координаты и скоростью её изменения. Это состояние системы можно отобразить точкой на плоскости с координатами , , называемой фазовой плоскостью. При изменении состояния системы изображающая точка перемещается на фазовой плоскости по кривым, которые называют фазовыми траекториями. Cовокупность фазовых траекторий, построенных для различных начальных условий, определяет все возможные процессы в системе и служит наглядным изображением её динамических свойств.

Для получения уравнения фазовых траекторий исключим из (8.2) время, поделив второе уравнение на первое:

(8.3)

Интегрирование нелинейного дифференциального уравнения (8.3) позволяет найти уравнение фазовой траектории:

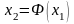. (8.4)