Дифференцирование функции, заданной неявно

Определение 1. Равенство F(x, y) = 0 определяет у как функцию у = у(х), задает эту функцию неявно.

Для нахождения производной функции у, заданной неявно, нужно продифференцировать равенство F(x, y) = 0 по аргументу х и решить уравнение относительно у'.

Примеры 1 – 4. Продифференцировать функцию у = у(х), заданную неявно.

1. х³ + у² - 5х = 0.

Решение. Продифференцируем это равенство:

(х³ + у² - 5х)' = 0;

3х² + 2уу' = 0;

Решим полученное равенство относительно у':

2. ху² + sin y – 2x = 3.

Решение. Продифференцируем равенство по х, считая у функцией по х:

(ху²)' + (sin y)’ – 2(x)’ = (3)’;

(х)' у² + х (у²)' + cos у  y’ – 2 = 0;

у² + х  2у  у' + cos y  y’ = 2;

Решим уравнение относительно у':

2х  у  у' + cos y  y’ = 2 - у² ;

у'(2х  у + cos y) = 2 - у²;

Пользуясь формулами и правилами дифференцирования, найдем производные следующих функций.

Пример 1. Найти производные следующих функций

Решение. Имеем:

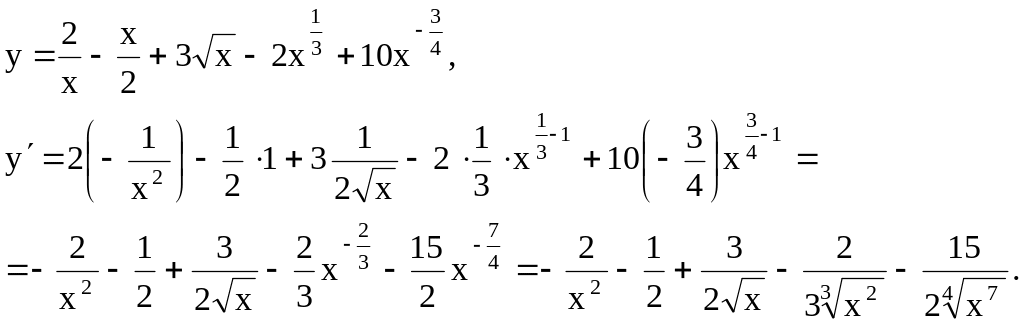
Пример 2. у = х² (cos x – 4 sin x).

Решение. Воспользуемся формулой 9 и таблицей производных.

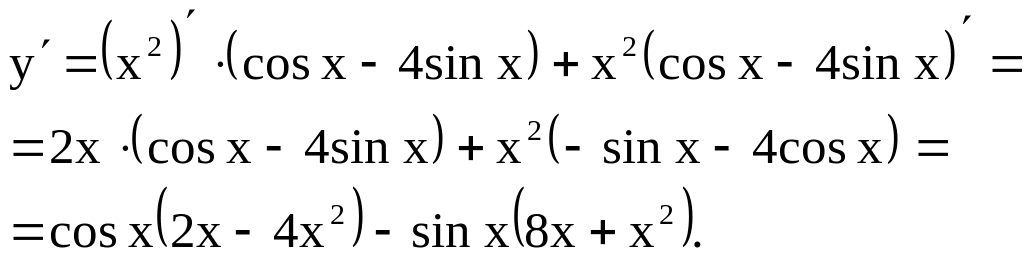
Пример 3. у = (3х² + 5х – 1)³.

Решение. Имеем сложную функцию, последнее действие производится над выражением u = 3х² + 5х – 1.

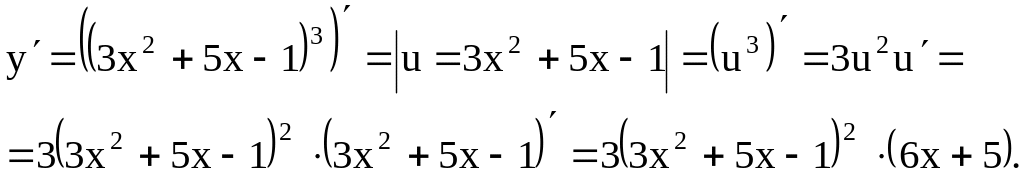
Пример 4. y = arctg⁸ x

Решение. Имеем сложную функцию, последнее действие – возведение в 8ую степень производится над u = arctg x.

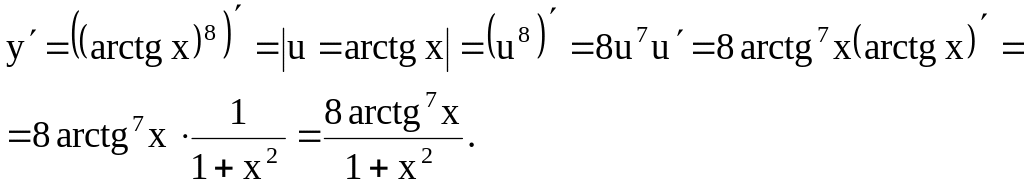
Пример 5. у =

Решение. Имеем дважды сложную функцию

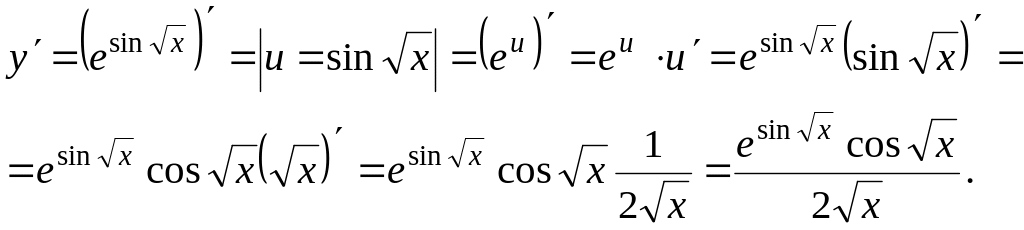
Пример 6.

Решение. Воспользуемся формулой 11

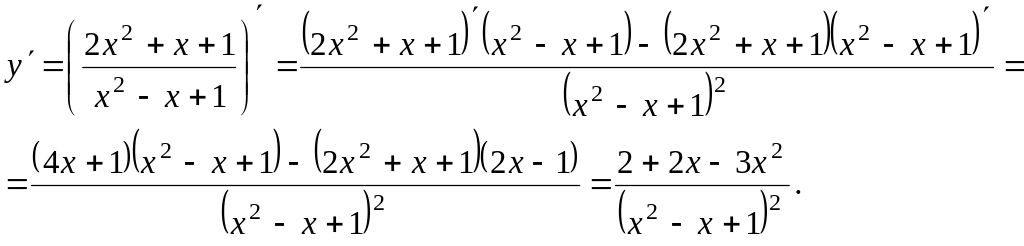
Пример 7. y = arctg (ln x) + ln (arctg x).

Решение. Имеем сумму двух сложных функций, воспользуемся правилами дифференцирования суммы функций, при вычислении значения функции в первом слагаемом последнее действие – (вычисление арктангенса) производится над логарифмом, значит, промежуточный аргумент – ln x, а во втором слагаемом (вычисление логарифма) – над arctg x, значит промежуточный аргумент – arctg x.

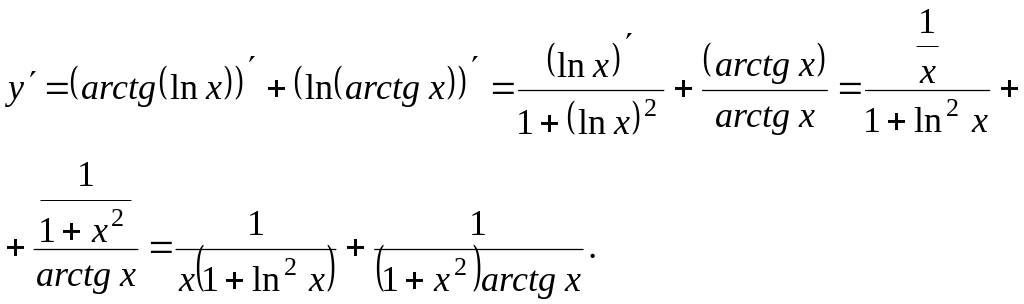
Пример 8.

Решение. Имеем функцию у = у(х), заданную неявно. Продифференцируем это равенство, считая, что sin y, e ^{– y} – сложные функции:

В левой части группируем слагаемые с у', в правую часть переносим слагаемые, не содержащие у'.

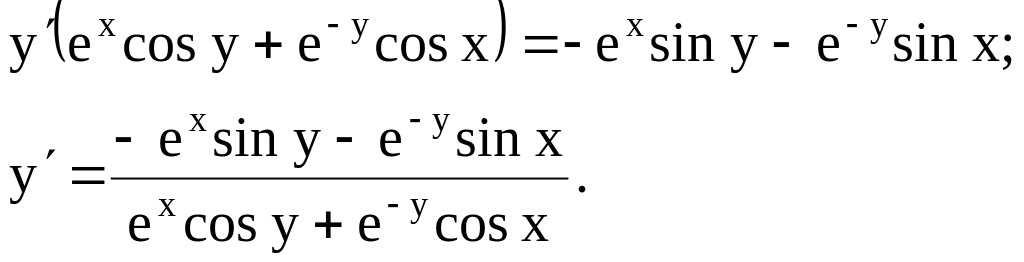
Пример 9. .

Решение. Имеем показательно-степенную функцию .

Прологарифмируем данное равенство:

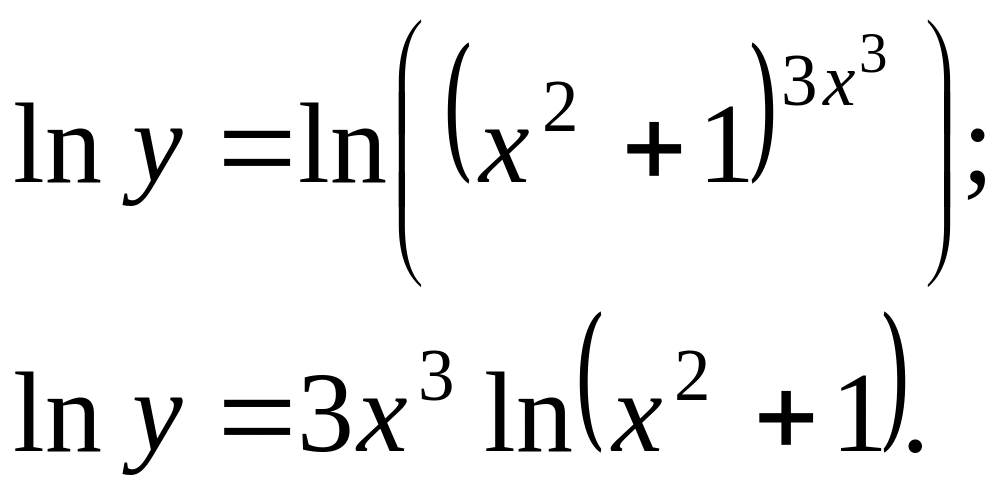
Продифференцируем данное равенство:

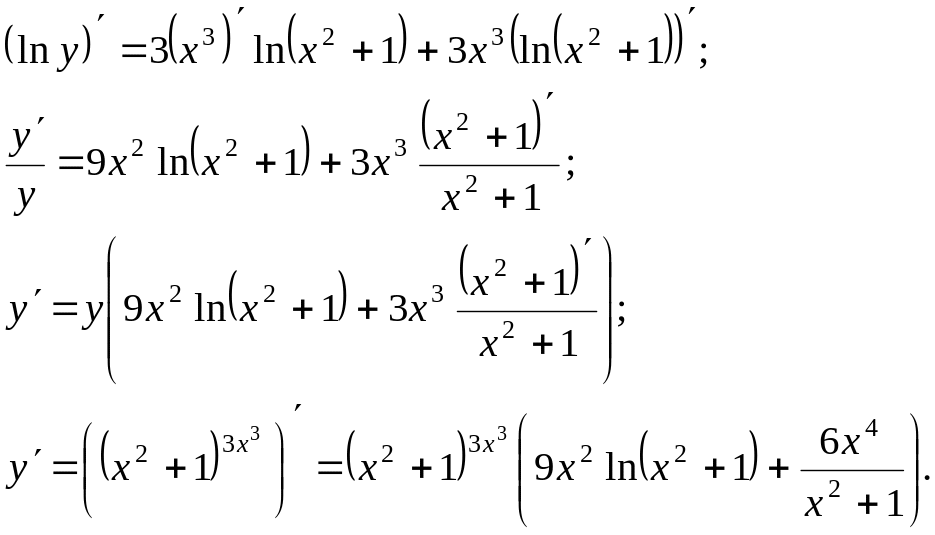
Дифференциал функции и его приложение

Пусть функция y = f(x) дифференцируема в точке х, тогда f ’(x) = , а по теореме о связи функции, имеющей предел и бесконечно-малой , т.е. приращение функции можно представить в виде двух слагаемых, одно зависит от х линейно, а второе содержит степени х не ниже второй.

Опр. 1. Дифференциалом функции называется главная часть ее приращения, линейная относительно приращения аргумента.

Обозначается: (34)

Для f (x) = x; dx = х, тогда dy = f ’(x)dx

Поэтому производную функции y = f(x) можно обозначить:

(35.)

Из определения (4.29) следует, что свойства дифференциалов аналогичны свойствам производной:

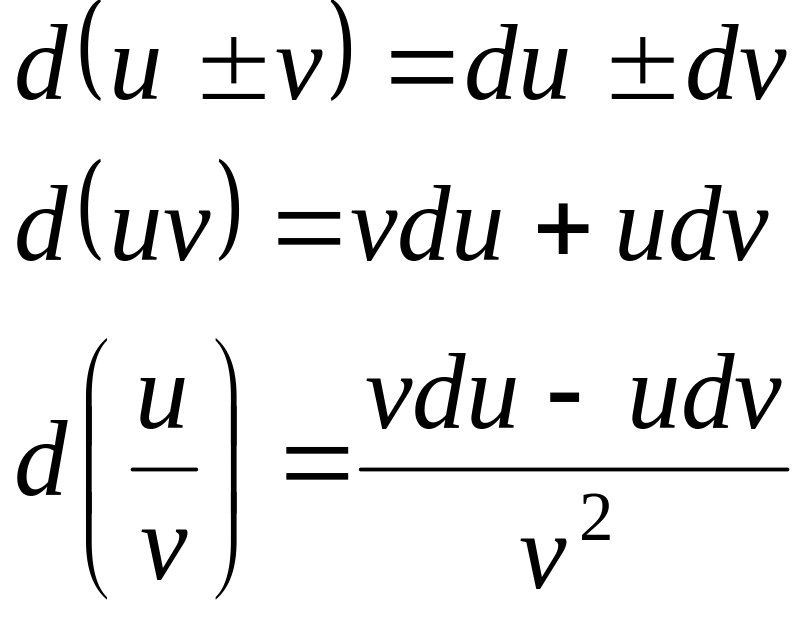
Приложения дифференциала основываются на приближенной формуле:

(36)

1. Приближенные вычисления.

Пусть известно значение функции y = f (x) в точке х₀, т.е. f (х₀). Тогда . Обозначим х = х₀ + х, получим

(37)

Пример. Вычислить приближенно значение

1) .

Решение. Имеем

х = 4,01; х = х - х₀=0,01.

Поэтому

3. 

Имеем f (x) = sin x; x=33⁰= , берем

sin 33⁰ = sin

2. Оценка погрешности.

Пусть имеем зависимость y = f (x), а х измеряется с ошибкой х, тогда у получит ошибку у:

.

Например, найдем ошибку при вычислении ln 2,1. Т.к. х = 2,1, то ошибка х = 0,05, f (x) = ln x; поэтому