Дифференцирование основных элементарных функций

1. Дифференцирование тригонометрических функций.

1 ) f(x)=sin x; f '(x)=(sin x)'=cos x (13.)

■ Имеем (sin x)'=

■

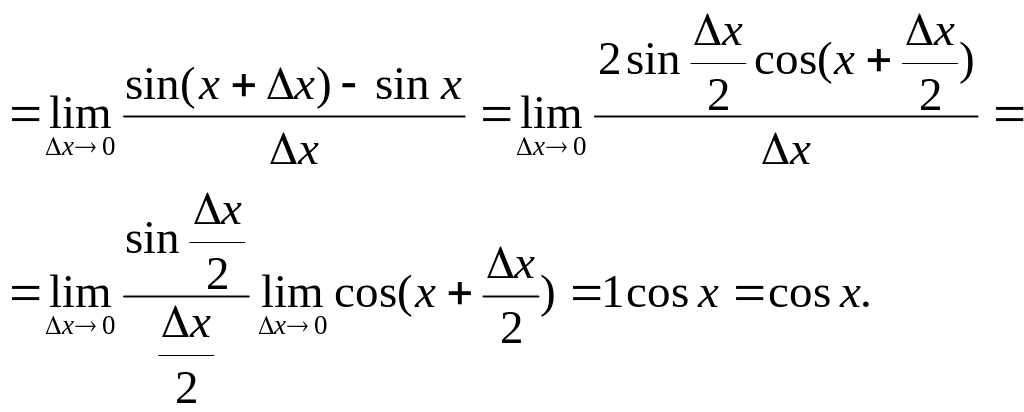
Здесь мы воспользовались первым стандартным пределом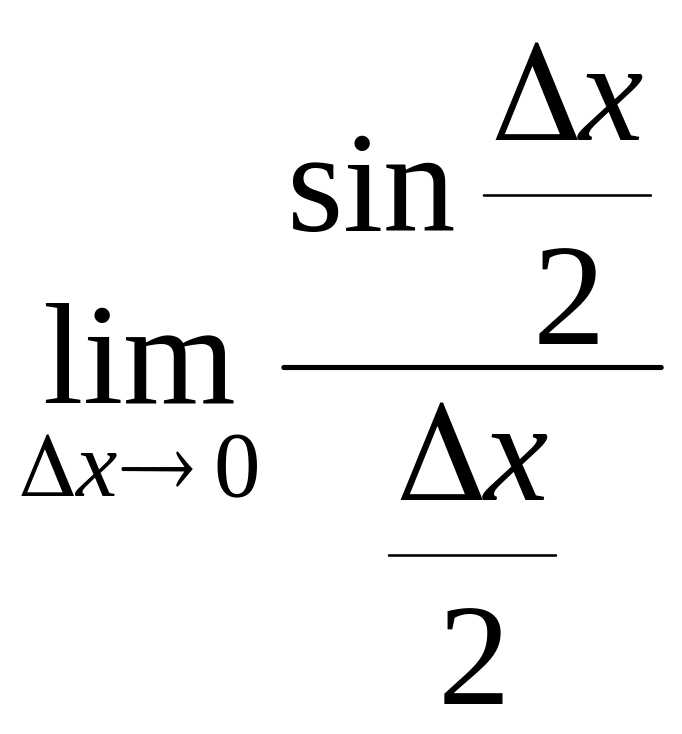 =1 и непрерывностью функции y = cos x.

2 ) (cos x)' = - sin x (14.)

Доказывается аналогично.

3 ) (tg x)' = (15.)

■ Воспользуемся формулой (4.11.) § 4.2.1.

у’ = (tg x)' = =

= .■

4 ) (сtg x)' = (16.)

Пример. Продифференцировать функцию 1) y = sin(x²); 2)y = sin²x.

Решение: 1) функция сложная, u=x² , поэтому воспользуемся правилом дифференцирования сложной функции:

y'(x)=(sin (x²))'=|u=x²|=(sin u)'=cos uu'= cos x²(2x)=2x cos x².

2) y'(x)=((sinx)²)'=|u=sin x|=(u²)'=2uu'= 2sin x(sin x)'=2sin xcos x= =sin 2x.

2. Дифференцирование логарифмической функции.

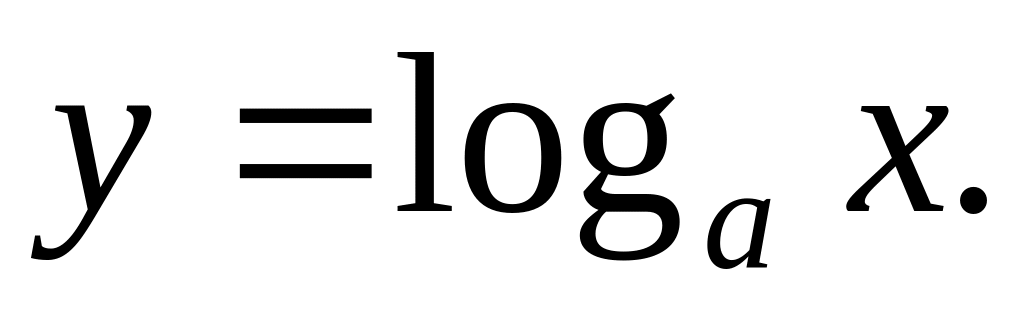
Имеем

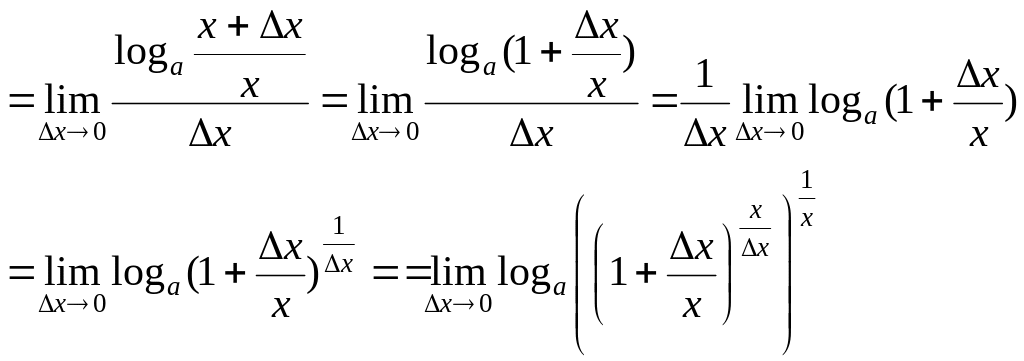
в силу непрерывности функции и второго стандартного предела = е, получим у' = по свойству логарифмов log _a e= . Поэтому у' = .

Значит (17.)

(18.)

Например:

1)

2)

3) |u=x²+3x+9|=(lnu)'= .

4) y = x²ln(3x+2). Воспользуемся формулой (9.)

y'=(x²ln(3x+2))'=(x²)'ln(3x+2)+x²(ln(3x+2))'= 2x ln(3x+2) + x² = = 2x ln(3x+2) + x² = 2x ln(3x+2) + .

Для нахождения производных других функций воспользуемся методом логарифмического дифференцирования: сначала функция логарифмируется с использованием формулы: ln y^k = k ln y (y>0), а потом дифференцируется сложная функция.

3. Дифференцирование степенной функции. y = x^,  R.

Пусть y = x^, тогда ln y = ln х^ =  ln х. Продифференцируем последнее равенство: (ln y)’ = ( ln х)’; ; отсюда

, т.е.

( х^)'=х^{ - 1} (20.)

Например: 1)

2)

3)

4) , т.е.

(21.)

5) , т.е.

(22.)

Здесь мы пользовались определением степени:

х ^-m = (23.) (24.)

4. Дифференцирование показательной функции. у = а^х

у = а^х; прологарифмируем это равенство: lnу = lnа^х и продифференцируем последнее равенство: (lnу)’ = (lnа^х)’; , т.к. ln a = с. Отсюда у' = y ln a, т.е. (25.)

Например, 1) ; 2) ; 3) , т.е.

(26.)

4)

5. Дифференцирование показательно-степенной функции у = u(x)^v(x).

Примером такой функции является функция . Применим метод логарифмического дифференцирования. Прологарифмируем эту функцию:

lny = ln ;

lny = x² ln ;

Продифференцируем последнее равенство по правилу дифференцирования сложной функции:

(ln y)'=(x²)'ln(lnx)+x²(ln(ln x))';

;

у' = ;

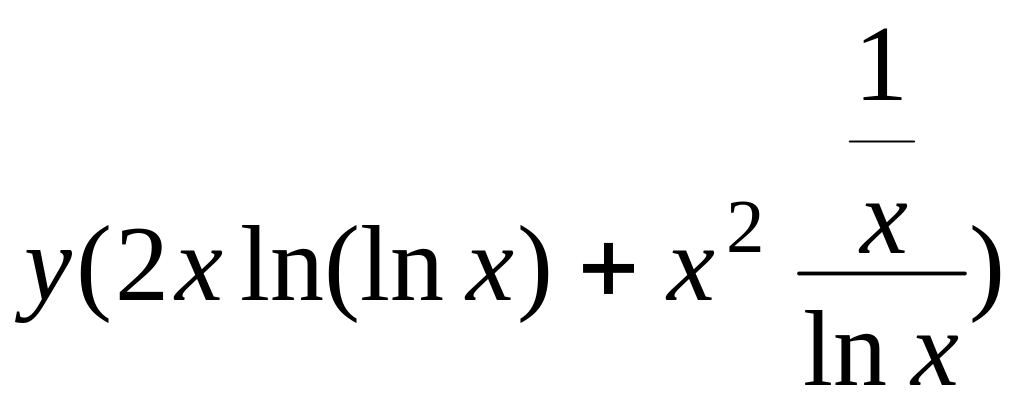у' = .

6. Дифференцирование обратных тригонометрических функций.

Пусть y = f(x) и x = (y) две взаимно обратные функции.

Теорема 1.(о дифференцировании обратных функций). Производные прямой и обратной функций связаны соотношением:

(27.)

■ Пусть y = f(x) и x = (y) – взаимно обратные функции. Рассмотрим сложную функцию y = f((y)) и продифференцируем ее по у. Промежуточный аргумент - х. По формуле (12.) имеем

, , а ■

Производные обратных тригонометрических функций:

(28.)

(29.)

(30.)

(31.)

Докажем, например формулу (28.)

■ Для функции y = arcsinx обратной является функция x = siny для х .

Поэтому

■

6. Дифференцирование гиперболических и обратных гиперболических функций.

Используя правила дифференцирования, получим и производные гиперболических функций. Имеем:

Полученные для основных элементарных функций результаты сведем в таблицу, рассматривая соответствующие функции как простые(слева) и сложные(справа).

Таблица производных.

№	y = f(x)	y = f(u(x))
1	(х)'=х - 1	(u)'=u - 1u'
2
3
4
5
6
7
8	(sin x)'=cos x	(sin u)'=cos u  u'
9	(cos x)'= - sin x	(cos x)'= - sin uu'
10	(tg x)' =	(tg u)' =
11	(ctg x)' =	(ctg u)' =
12
13
14
15
16	(sh x)' = ch x	(sh u)' = ch uu'
17	(ch x)' = sh x	(ch u)' = sh uu'

Замечание. Справедливы формулы: (32.)

(33.)

Например,

1. .

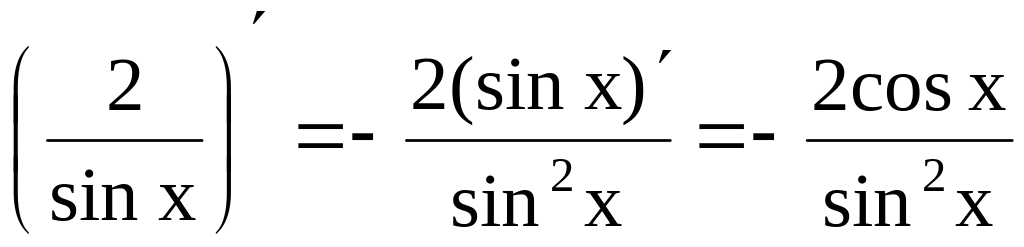2)