Натуральный логарифм и гиперболические функции.

Определение 21.1. Логарифм с основанием е называется натуральным логарифмом.

Обозначение: log_ex=ln x.

Определение 21.2. Функции (гиперболический синус), (гиперболический косинус), (гиперболический тангенс) и (гиперболический котангенс) называются гиперболическими функциями.

Замечание 1. Гиперболические функции обладают некоторыми свойствами, похожими на свойства обычных тригонометрических функций. Например,

сh²x – sh²x = ¼(e^2x + 2 + e^-2x - e^2x + 2 - e^-2x)=1,

2 shx chx = 2 = =sh2x,

thx=shx/chx, cthx=chx/shx,

thx·cthx = =1 и т.д.

Замечание 2. Термин «гиперболические» объясняется тем, что уравнения

x = a ch t, y = a sh t, a>0,

являются параметрическими уравнениями правой ветви гиперболы x² - y² = a², так же, как x = a cost, y = a sint (0≤t≤2π) – параметрические уравнения окружности x²+y²=a².

Лекция 22. Комплексные числа.

Определение комплексного числа.

Определение 22.1. Комплексным числом будем называть упорядоченную пару действительных чисел , записанную в форме , где - новый объект ("мнимая единица"), для которого при вычислениях полагаем .

Первая компонента комплексного числа , действительное число , называется действительной частью числа , это обозначается: ; вторая компонента, действительное число , называется мнимой частью числа : .

Определение 22.2. Два комплексных числа и равны тогда и только тогда, когда равны их действительные и мнимые части: .

Множество комплексных чисел неупорядочено, т.е. для комплексных чисел не вводятся отношения "больше" или "меньше".

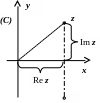
Геометрически комплексное число изображается как точка с координатами на плоскости. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью С.

Определение 22.3. Суммой двух комплексных чисел и называется комплексное число , определяемое соотношением , т.е. , .

Это означает, что геометрически комплексные числа складываются как векторы на плоскости, покоординатно.

Определение 22.4. Произведением двух комплексных чисел и называется комплексное число , определяемое соотношением , т.е. .

Для двух комплексных чисел с нулевой мнимой частью и получим , , т.е. для множества комплексных чисел с нулевой мнимой частью операции сложения и умножения не выводят за пределы этого множества. Отождествим каждое такое число с действительным числом , равным действительной части комплексного числа, т.е. будем считать, что . Теперь действительные числа - подмножество множества комплексных чисел С. Числа с нулевой действительной частью, т.е. числа вида , называются мнимыми числами.

Определение 22.5. Число называется числом, сопряжённым к числу . Часто сопряжённое число обозначается также символом .

Определение 22.6. Действительное число называется модулем комплексного числа .

Геометрически модуль числа z - длина радиуса вектора точки z; модуль разности чисел и равен расстоянию между этими точками: .

Найдём произведение сопряжённых чисел:

.

Таким образом, - всегда неотрицательное действительное число, причём .

Для нахождения частного комплексных чисел домножим числитель и знаменатель на число, сопряжённое знаменателю: .

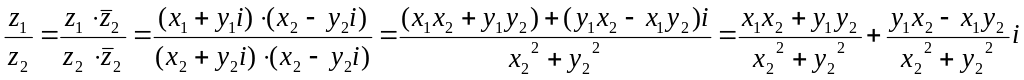Примеры. Выполнить арифметические действия с комплексными числами , .

;

; .

Тригонометрическая форма комплексного числа

Запись комплексного числа в виде называется алгебраической формой комплексного числа. Изобразим число как точку на плоскости с декартовыми координатами .

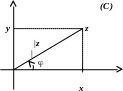
Если теперь перейти к полярным координатам , то , поэтому . Угол называется аргументом комплексного числа и обозначается : . Аргумент комплексного числа определён неоднозначно (с точностью до слагаемых, кратных ): если, например, , то значения , равные и т.д. тоже будут соответствовать числу , поэтому значение аргумента, удовлетворяющее условиям , будем называть главным; для обозначения всех значений аргумента комплексного числа применяется символ : .

Запись комплексного числа в виде

называется тригонометрической формой числа.

Число - единственное число, модуль которого равен нулю; аргумент для этого числа не определён.

Переход от тригонометрической формы к алгебраической: . Формулы для перехода от алгебраической формы к тригонометрической таковы:

При решении задач на перевод алгебраически заданного комплексного числа в тригонометрическую форму следует изобразить это число на комплексной плоскости С и, таким образом, контролировать полученный результат.

Примеры: записать в тригонометрической форме числа

.

.

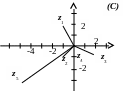
В тригонометрической форме легко интерпретируются такие действия, как умножение, деление, возведение в степень. Пусть , , . Тогда

Вывод: при умножении комплексных чисел их модули перемножаются, аргументы складываются.

Если , то , т.е. операция сопряжения не меняет модуль числа, и изменяет знак его аргумента, поэтому .

Вывод: при делении комплексных чисел их модули делятся друг на друга, аргумент частного равен разности аргументов делимого и делителя.

Показательная форма комплексного числа

Ряд Маклорена для функции сходится к функции при любом действительном х. Запишем это разложение для :

Степени числа : .

В круглых скобках стоят ряды для и , которые сходятся для любого действительного ; поэтому получаем . Эта формула называется формулой Эйлера. Теперь любое комплексное число можно представить как

;

эта форма записи называется показательной. В этой форме умножение и деление комплексных чисел выполняются и интерпретируются также легко, как и в тригонометрической:

.

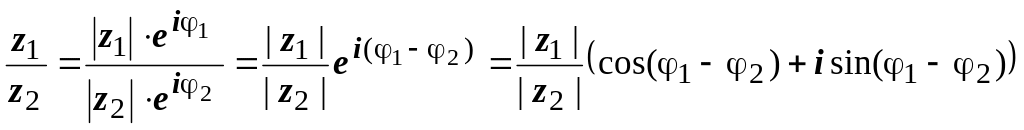Индукцией по показателю степени легко доказывается формула Муавра: если , то , или, в показательной форме, .

С помощью этой формулы легко вычислять высокие степени комплексных чисел.

Пример. Упростить.

.

В заключение рассмотрим операцию извлечения корня -ой степени из комплексного числа . По определению, любое число , такое, что , называется корнем -ой степени из числа . Пусть , . Тогда . Числа равны, если равны их модули и аргументы, поэтому , , откуда , , при этом различных значения корня -ой степени из числа получаются при .

Пример: найти все значения .

Число в тригонометрической форме имеет вид . Все пять значений корня даются формулой , при . Они расположены на окружности радиуса . Значение, соответствующее , имеет аргумент , остальные расположены с интервалом по , равным , в вершинах правильного пятиугольника, вписанного в эту окружность.

Лекция 23.

Разложение дроби на простейшие.

1. Разложение многочлена на множители.

Функция f(x) = где n – целое число, называют многочленом n – ой степени.

Определение: Корнем многочлена n – ой степени называют такое значение переменного х при котором многочлен обращается в нуль.

Если х = а – корень многочлена, то многочлен f(x) делится на разность х – а

без остатка, т.е. представляется в виде произведения:

Теорема 1. Всякий многочлен n – ой степени разлагается на n+1 линейных множителей, первым из которых является множитель, равный коэффициенту при х ⁿ

Пример.

Многочлен f(x) = х³ – 6х² + 11х – 6 при х = 1 обращается в нуль, поэтому по теореме 1 делится без остатка на разность х –1.

х ³ – 6х² + 11х – 6 х - 1

х² – 5х + 6

- 5х² + 11х

- 5х² 5х

6х - 6

6х - 6

0

f(x) = (х - 1)(х² – 5х +6) = (х - 1)(х - 2)(х - 3)

(Квадратный трехчлен разлагается на множители).

Теорема 2. Целые корни многочлена

f(x) = хⁿ + A₁x^n-1 + A₂х^n-2 +…+А_n

находятся среди делителей свободного слагаемого.

Пример. Разложить многочлен на множители

f(x) = х³ – 5 х + 8 х – 4

Найдем корни многочлена, т.е. решим уравнение

х³ – 5 х + 8 х – 4 = 0

Выпишем делители свободного слагаемого (– 4):

1; 2; 4

х = 1 – один из корней многочлена, т.е. данный многочлен должен делиться на разность х – 1 без остатка.

Х³ – 5 х² + 8 х - 4 х – 1

Х³ – х² х² – 4х + 4

• 4х² + 8х

• 4х² + 4х

4х - 4

4х - 4

0

В результате многочлен разложился на множители:

Х³ –5х² + 8х – 4 = (х - 1)(х² – 4х + 4)=(х -1)(х - 2)² = (х - 1)(х - 1)(х - 1).

Если многочлен имеет корень кратности k, то считается, что многочлен имеет k одинаковых корней.

Теорема 2. Всякий многочлен степени n имеет ровно n корней (действительных или мнимых).