2. Расчетная часть

1. Задание

Расчетная часть включает 2 задачи. Для каждой из них необходимо получить:

1. Составить таблицу исходных данных.

2. Прогноз изменения данных, выполненный с использованием экспоненциальной регрессии.

3. Коэффициенты в уравнениях экспоненциальной кривой.

4. Погрешности вычислений. Оценить, какой тип регрессии наилучшим образом подходит для расчета.

2. Задачи для исследования:

1. Определить минимальный необходимый тираж ежемесячного журнала “Обо всем по немного” и возможный доход от размещения в нем рекламы в следующем месяце, если известны данные об объемах продаж этого журнала и доходах от размещения рекламы за предшествующие 12 месяцев (считать, что расценки на рекламу не менялись).

2. В целях привлечения покупателей и увеличения оборота фирма проводит стратегию ежемесячного снижения цен на свой товар. На основании данных о динамике изменения цен и объемов продаж в данной фирме, а так же еще трех конкурирующих фирмах за последние 12 месяцев сделать прогноз о том, возрастет ли объем продаж у данной фирмы при очередном снижении цен в следующем месяце, если предположить, что цены и объемы у конкурентов в следующем месяце будут средние за рассматриваемый период.

3. Выполнение задания 1

Составим таблицу для первой задачи (См. Рис. 1).

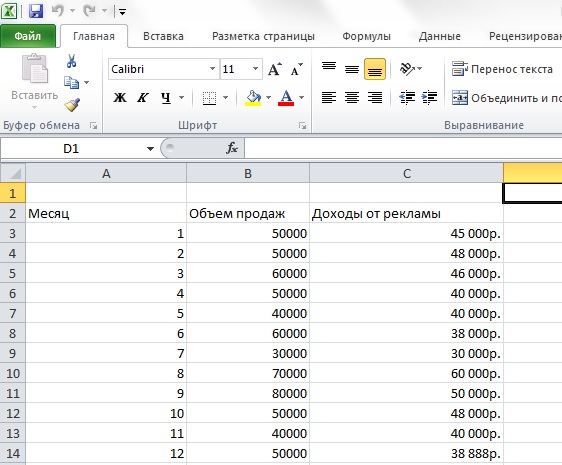
Рисунок 1- Исходная таблица

Используя линейную и экспоненциальную регрессию, составим прогноз изменения данных. Для этого нам понадобится найти новое значение для независимой переменной и зависимой, используя функцию ТЕНДЕНЦИЯ (смотреть рисунок 2).

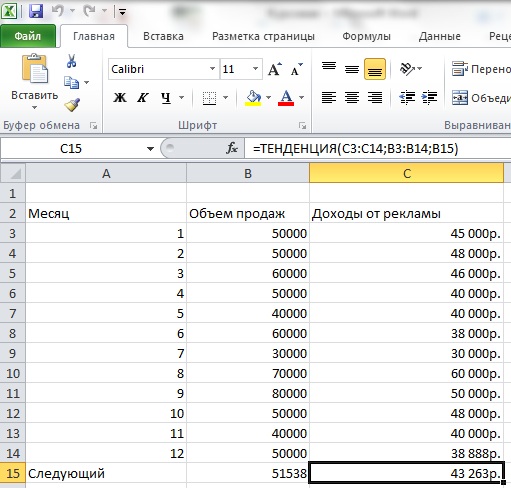
Рисунок 2 - Использование функции ТЕНДЕНЦИЯ

Для экспоненциальной регрессии используем функцию РОСТ.

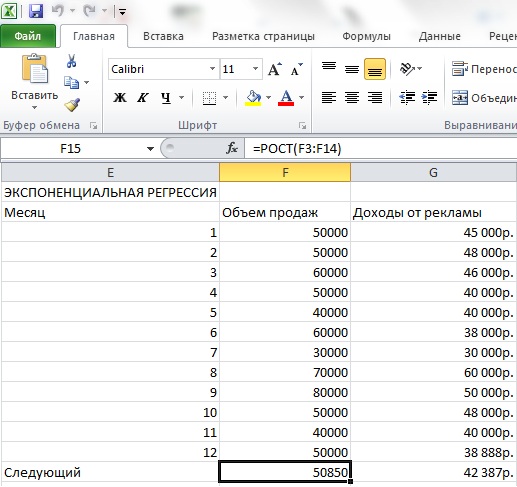
Рисунок 3 - Использование функции РОСТ

Найдем коэффициент b. Для линейной регрессии воспользуемся формулой =ЛИНЕЙН(C3:C15;B3:B15;ЛОЖЬ), для экспоненциальной - =ЛГРФПРИБЛ(G3:G15;F3:F15;ЛОЖЬ). В результате получим для линейной регрессии значение b равное 1, для экспоненциальной 1.

Погрешность регрессии находится командой СТОШУХ() для линейной и экспоненциальной регрессии. Лучше всего подходит тип регрессии, у которой погрешность меньше.

Для построения линии тренда, выделим диаграмму, откроется вкладка Макет. Далее выберем Линия тренда и выберем экспоненциальное приближение для диаграммы с экспоненциальной регрессии (См. Рис. 4).

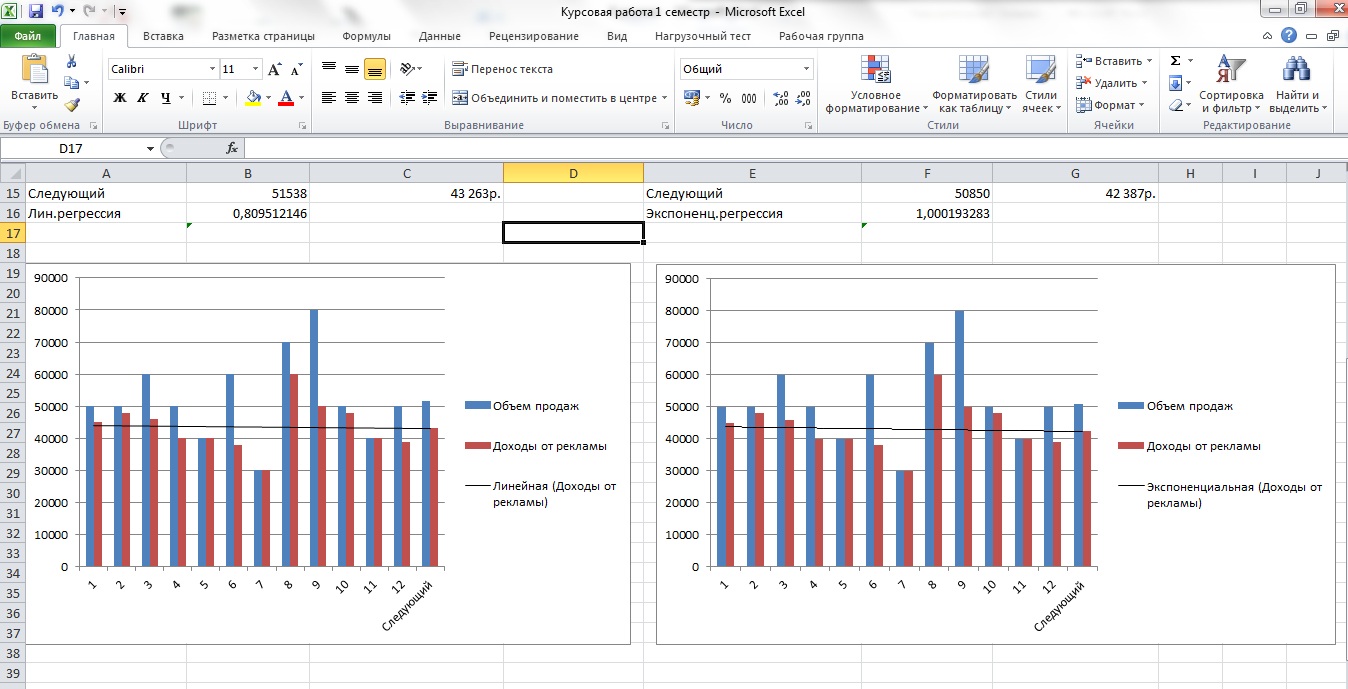
Рисунок 4 - Линейная и экспоненциальная регрессии

4. Выполнение задания 2

Чтобы выполнить это задание нам понадобится найти новое значение переменной. Воспользуемся командой СРЗНАЧ.

Коэффициенты находятся таким же способом, но в этой задаче меняется параметр СТАТИСТИКА.

=ЛГРФПРИБЛ(G3:G15;F3:F15;;ИСТИНА) – экспоненциальная регрессия.

Заключение

На основании результатов вычислений, полученных с помощью функций ЛГРФПРИБЛ(), можно написать уравнение экспоненциальной кривой для простой и множественной регрессии.

Простая регрессия (Задание 1):

• Экспоненциальная регрессия:

y= 1,008282477^x

Множественная регрессия (Задание 2):

• Экспоненциальная регрессия:

24381,08164 * (0,99967124^x) * (1,000002331^x) * (1,00026737^x) х х (0,999977126^x) * (1,00013664 ^x) * (0,99998269 ^x) * (1,00003823 ^x)

Погрешность вычислений для каждого коэффициента в уравнении экспоненциальной кривой.

Чтобы найти погрешность для коэффициентов воспользуемся регрессионной статистикой.

• Экспоненциальная регрессия: Стандартная ошибка для x 0,52975662