Основи системного аналізу об’єктів та процесів комп’ютеризації
Приклади типових завдань
Предмет, методи і завдання дисципліни.
Інформаційна міра адекватності. Розгляд асимптотичних випадків.
Синтез логічних схем на основі логічних формул.
Основні етапи системного аналізу і моделювання систем.
Структурний аналіз систем. Декомпозиція систем.
Логічні функції.
Рівні моделювання: структурне (імітаційне), логічне, кількісне моделювання. Методи моделювання.
Формула розкладу за змінними.
Характеристика систем масового обслуговування. Аналітичний метод аналізу СМ (рівняння Колмогорова).
Оцінка якості функціонування складних систем. Основні задачі дослідження систем – аналіз і синтез.
Дискретно-стохастичні моделі (Р-схеми). Подання математичної моделі.
Означення логічної функції, формули реалізації функції.
Машина Тюрінга. Обчислення функцій на машині Тюрінга.
Методи спрощення моделей. Адекватність моделі і об’єкта.
Пристрої з необмежено пам’яттю. Основні властивості алгоритмів.
Моделювання систем
Приклади типових завдань.
Пояснити суть принципу системності в моделюванні систем та дати загальна характеристику проблем моделювання.
Навести класифікація видів моделювання.
Дати характеристику основних принципів побудови математичних моделей.
Дати визначення марківського ланцюга та навести основні його властивості.
Отримати математичну модель процесів народження і загибелі. Приклад застосування моделі для дослідження простих комп’ютерних мереж. Обчислення ергодичних ймовірностей станів системи.
Математичні моделі консервативних систем масового обслуговування (МО). Обчислення інтенсивностей переходів марківських процесів.
Навести приклад консервативної системи МО.
Дати класифікацію основних типів систем МО. Символіка систем МО.
Навести математичні моделі основних типів систем МО:
система із втратами;
багатолінійна система з обмеженою чергою і обмеженим часом очікування;
багатоканальна система з обмеженою чергою;
багатоканальна система МО з необмеженою чергою і обмеженим часом очікування;
багатоканальна система з необмеженою чергою.
Особливості і область застосування імітаційного моделювання комп’ютерних мереж.
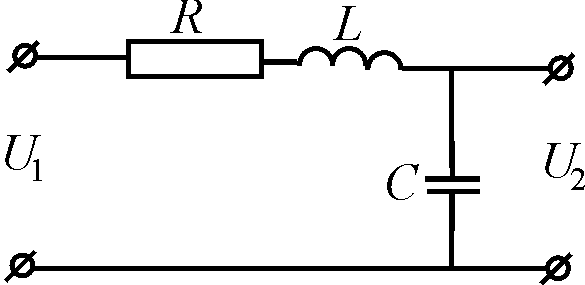
Створити математичну модель системи, принципіальна схема якої наведена на рисунку, та знайти її розв'язок за умови, що R=40 Ом, L=25 мГн, C=50 мкФ ;
Рисунок 1 – Принципіальна схема електричного фільтра
.
12.
Створити математичну модель системи,
принципіальна схема якої наведена на
рисунку, та знайти її розв'язок за умови,
що R=50 Ом,
L=35 мГн,
C=50 мкФ
;
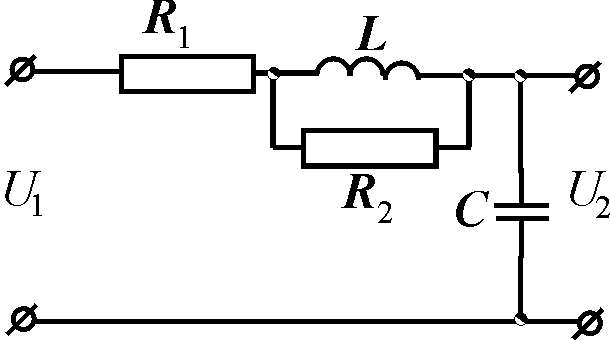
Рисунок 2 – Принципіальна схема електричного фільтра
13. Побудувати граф автомата Мілі робота, якого задана таблицею. За отриманим графом побудувати матрицю з’єднань
|
|
|||
|
|
|
|
|
Переходи |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Виходи |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. Побудувати граф автомата Мілі робота, якого задана таблицею. За отриманим графом побудувати матрицю з’єднань
|
|
|||
|
|
|
|
|
Переходи |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Виходи |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. Побудувати граф автомата Мура робота, якого задана таблицею. За отриманим графом побудувати матрицю з’єднань
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. Побудувати граф автомата Мура робота, якого задана таблицею. За отриманим графом побудувати матрицю з’єднань
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. Р - автомат заданий матрицею переходів.
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
1 |
1 |
Побудувати граф переходів Р – автомата та знайти ймовірність появи одиниці на виході автомата.
18. Р - автомат заданий матрицею переходів.
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
Побудувати граф переходів Р – автомата та знайти ймовірність появи одиниці на виході автомата.
19. Рівняння, що описують систему МО з кінцевим числом станів, мають такий вигляд
.
Скласти
інфінітезимальну матрицю А,
якщо
N=2,
а
,
і
для інших значень i
та
j.
Крім того
,
;
.
Знайти матрицю перехідних ймовірностей,
якщо
,
,
а
,
де І
– одинична матриця.
20. Рівняння, що описують систему МО з кінцевим числом станів, мають такий вигляд
.
Скласти
інфінітезимальну матрицю А,
якщо
N=2,
а
,
і
в інших випадках. Крім того
,
;
.
Знайти
матрицю перехідних ймовірностей, якщо
,
,
а
,
де І
– одинична матриця.
21. Багатоканальна система МО має N приладів і буфер нескінченної ємності. В будь-який момент часу t в системі можуть одночасно обслуговуватись не більше N вимог.
На вхід системи поступає потік вимог з експоненціальним законом розподілу з параметром . Обслуговування заявок, які поступають в систему МО, здійснюється у відповідності з принципом FCFS (First Come First Served – перший прийшов – першим обслужений). Тривалість обслуговування – випадкова величина з експоненціальним розподілом, параметр якого . Тривалість перебування в черзі випадкова незалежна від інших факторів величина, яка має експоненціальний закон розподілу з параметром . Необхідно за заданими значеннями =1.5 1/с, =1,2 1/с і =0,8 1/с обчислити аналітичним способом ергодичні розподіли системи МО.
22. Багатоканальна система МО має N приладів і буфер ємністю n, так що в будь-який момент часу t в системі можуть одночасно обслуговуватись не більше N вимог і не більше n заявок знаходитись в черзі. Одночасно в системі може знаходитись не більше ніж N+n вимог.
На вхід системи поступає потік вимог з експоненціальним законом розподілу з параметром . Обслуговування заявок, які поступають в систему МО, здійснюється у відповідності з принципом FCFS (First Come First Served – перший прийшов – першим обслужений). Тривалість обслуговування – випадкова величина з експоненціальним розподілом, параметр якого . Тривалість перебування в черзі випадкова незалежна від інших факторів величина, яка має експоненціальний закон розподілу з параметром .
Необхідно за заданими значеннями =1.3 1/с, =1,0 1/с і =0,85 1/с обчислити аналітичним способом ергодичні розподіли системи МО.