3.6. Исходный код функции: главная функция main

int main() {

setlocale(LC_ALL,"Russian");

cout <<"Введите начальное значение x0=" ; cin >> x0; cout<< endl;

cout <<"Введите начальное значение y=" ; cin >> y; cout<< endl;

cout <<"Введите начальное значение xn=" ; cin >> xn; cout<< endl;

cout <<"Введите количество интервалов n1=" ; cin >> n1; cout<< endl;

//Расчет шага h1

h1=(xn-x0)/n1;

cout<< "Шаг h1 равен "<< h1 <<endl;

n2=2*n1;

cout<< "Количество интервалов n2 равно "<< n2 <<endl;

//Расчет шага h2

h2=(xn-x0)/n2;

cout<< "Шаг h2 равен "<< h2 <<endl;

t=Eilera( x0, y, xn, h1, n1);

cout<< "Результат расчета по методу Эйлера y="<<t<<endl;

t1=Runge( x0, y, xn, h2, n2);

cout<< "Результат расчета по методу Рунге y="<<t1<<endl;

t2=2*t1-t;

cout<< "Утосненное решение с помощью формулы Рунге t2="<<t2<<endl;

t3=Runge_Kutte3( x0, y, xn, h1, n1);

cout<< "Результат расчета по методу Рунге-Кутты 3-го порядка y="<<t3<<endl;

t4=Uluchshennii_metod_Eilera( x0, y, xn, h1, n1);

cout<< "Результат расчета по Улучшенному методу Эйлера y="<<t4<<endl;

system("pause");

return 1;

}

Результат работы приложения

4.1. При n=5, Y₀=1, X₀=0, X_k=0,5,

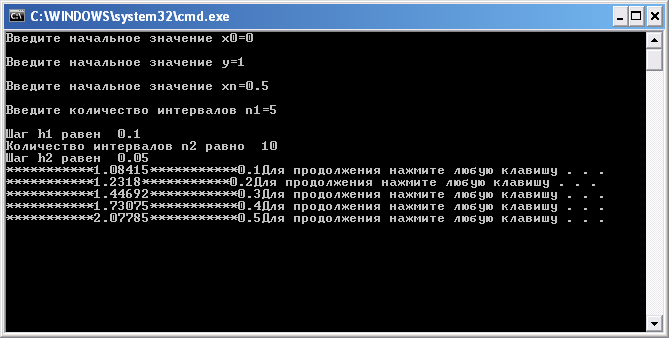
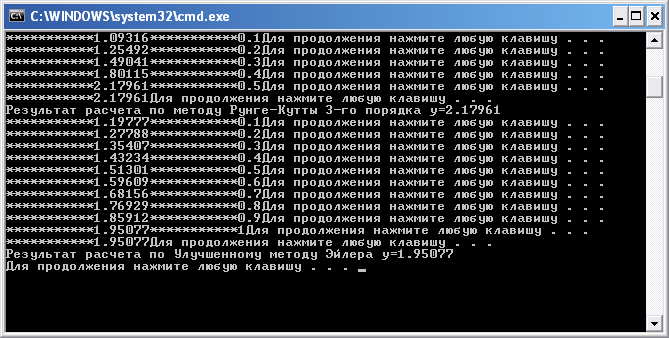
4.2. При n=10, Y₀=1, X₀=0, X_k=0,5,

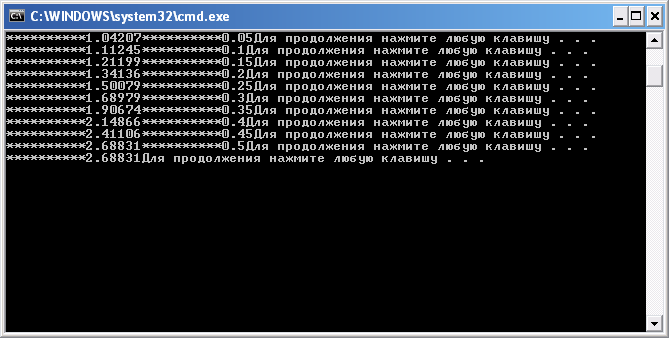
Заключение

По результатам выполненной работы можно сделать вывод, что решение дифференциального уравнения Коши 1-го порядка методом Эйлера является методом вычисления со средней точностью и точность вычисления данного метода (а также и других, более точных методов) зависит от количества разбиений интервала интегрирования. При сравнении результатов, полученных различными методами, можно сказать, что они сходятся с небольшой погрешностью, исходя из этого, можно сделать вывод, что необходимые алгоритмы были реализованы правильно.