6.2. Элементарные переключательные (логические) функции двух переменных

Рассмотрим все функции двух переменных (табл. 25).

Таблица 25

Переключательные функции двух переменных

		20	21	22	23
		Набор				Название	Формула
20	х1	0	1	0	1	функции
21	х2	0	0	1	1
	f0	0	0	0	0	Константа 0	0
	f1	1	0	0	0	Функция Пирса (Вебба), «стрелка Пирса», ИЛИ-НЕ	х1¯х2=
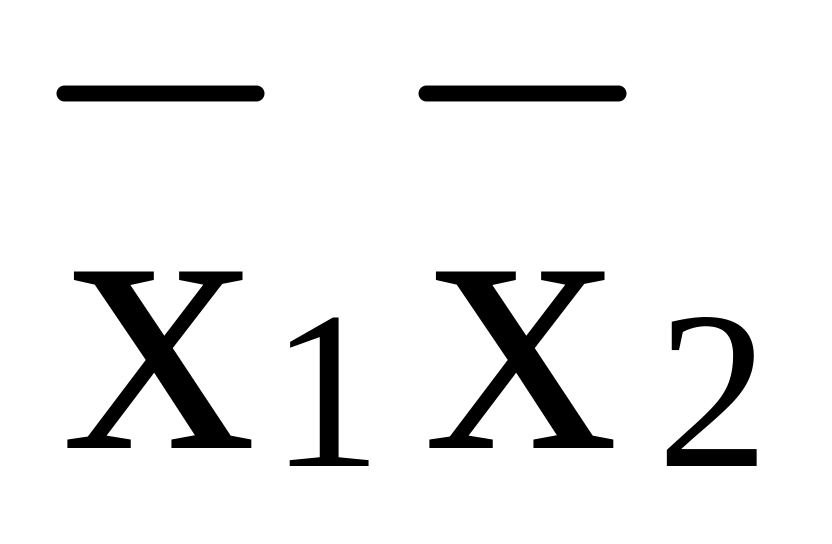
	f2	0	1	0	0	Запрет х2
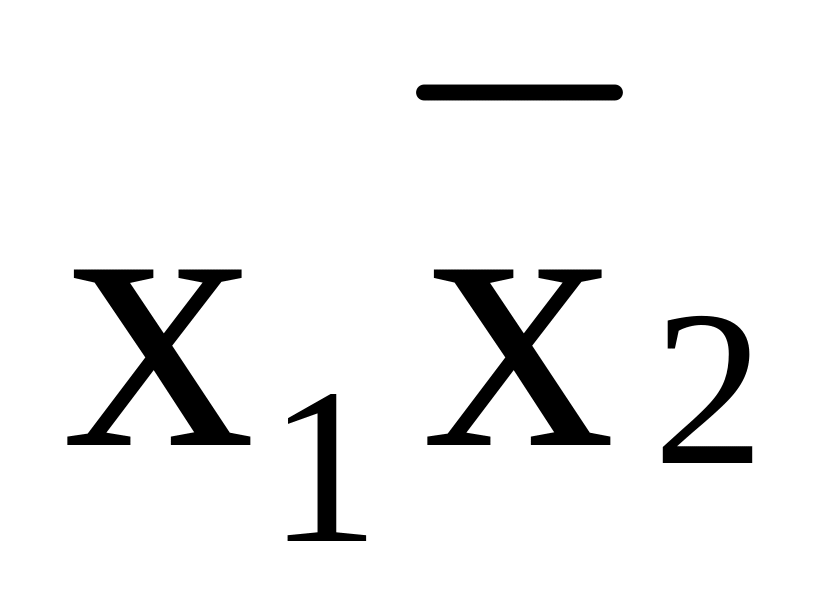
	f3	1	1	0	0	Отрицание х2
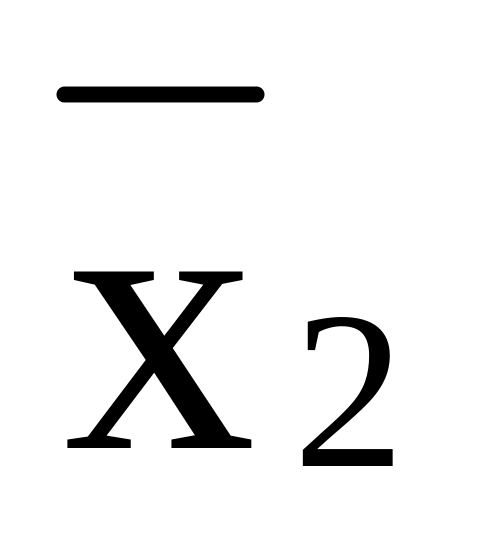
	f4	0	0	1	0	Запрет х1
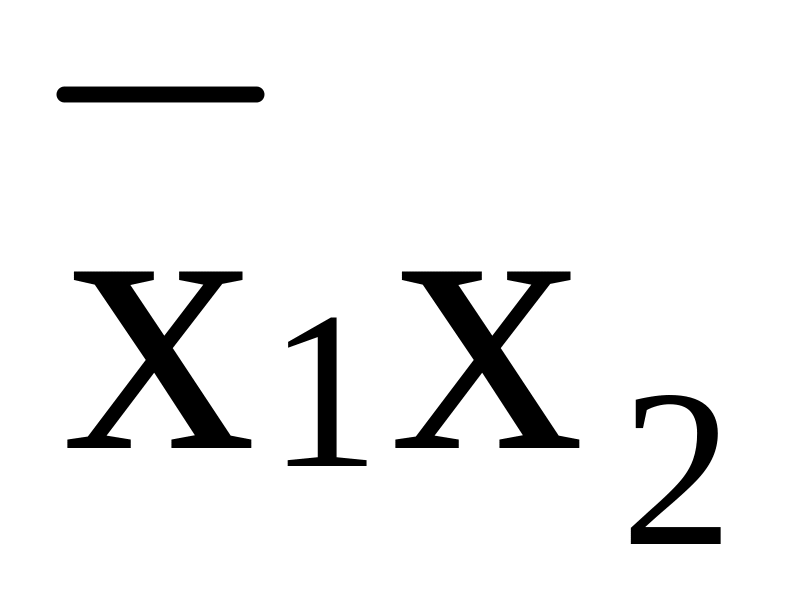
	f5	1	0	1	0	Отрицание х1
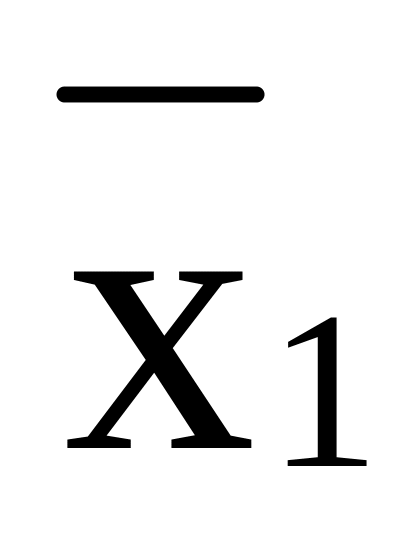
	f6	0	1	1	0	Сложение (сумма) по mod2	х1Åх2=
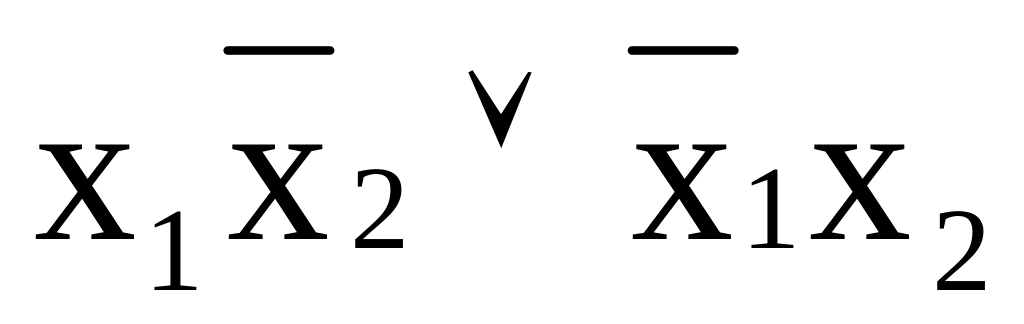
	f7	1	1	1	0	Функция Шеффера, «штрих Шеффера», И-НЕ	х1|х2=
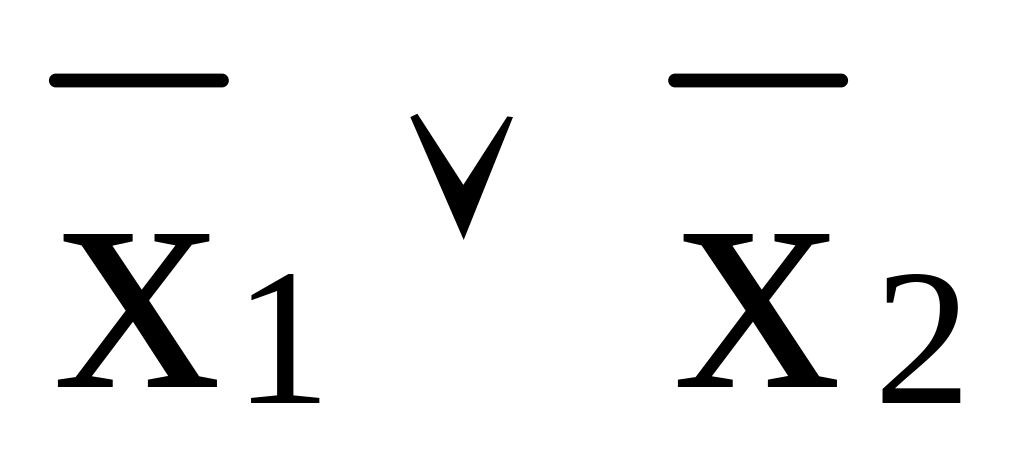
	f8	0	0	0	1	Конъюнкция, И	х1х2
	f9	1	0	0	1	Эквиваленция (эквивалентность)	х1«х2=
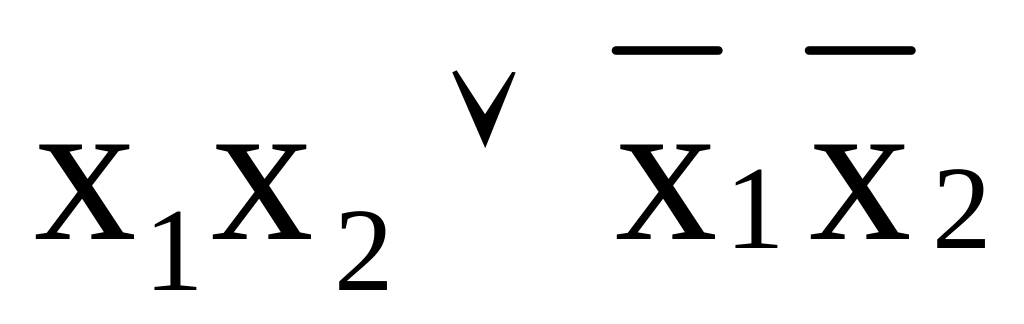
	f10	0	1	0	1	Повторение х1	х1
	f11	1	1	0	1	Импликация х2 в х1	х2®х1
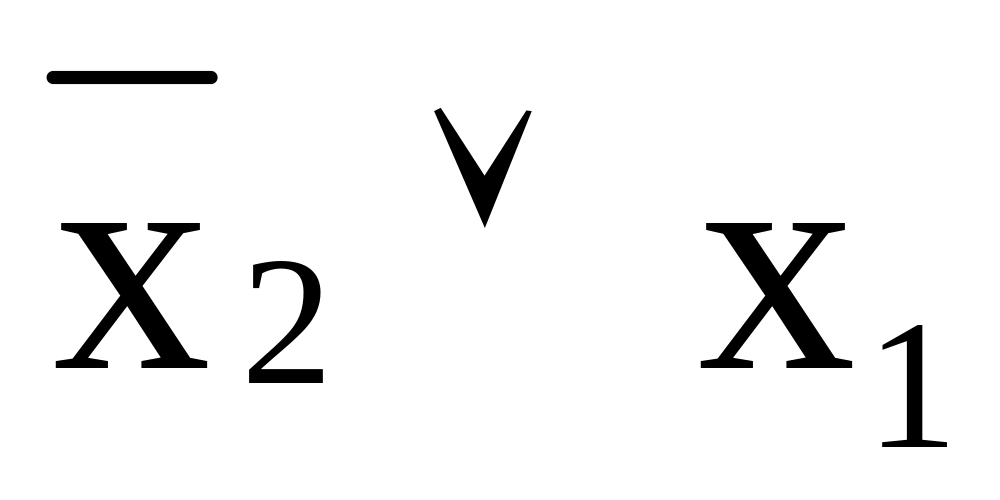
	f12	0	0	1	1	Повторение х2	х2
	f13	1	0	1	1	Импликация х1 в х2	х1®х2
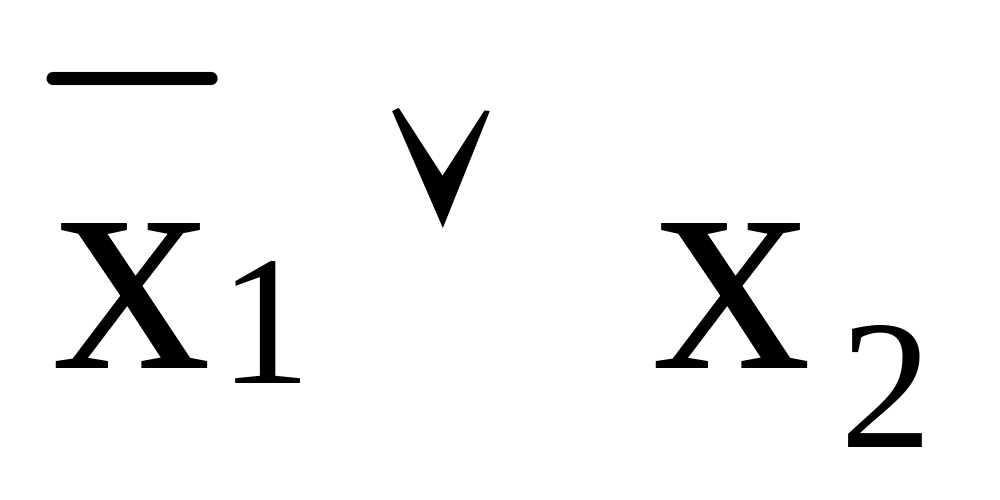
	f14	0	1	1	1	Дизъюнкция, ИЛИ	х1Úх2
	f15	1	1	1	1	Константа 1	1

Всего таких функций имеется 2²²=2⁴=16. Есть функции, зависящие только от одной переменной. Есть функции, не зависящие от переменных, – константы 0, 1. Такие функции называют вырожденными:

f₃(x₁x₂)= ; f₅(x₁x₂)= ; f₁₀(x₁x₂)=х₁; f₁₂(x₁x₂)=х₂;

f₀(x₁x₂)=0; f₁₅(x₁x₂)=1.

Некоторые функции мы тоже уже знаем: конъюнкцию f₈(x₁x₂)=х₁х₂ (точку между х₁ и х₂ опускаем); эквиваленцию (эквивалентность) f₉(x₁x₂)=х₁«х₂=х₁х₂Ú (здесь эквиваленция представлена в виде дизъюнкции двух конъюнкций, что можно доказать, составив таблицу истинности); импликацию f₁₁(x₁x₂)=х₂®х₁= Úх₁, f₁₃(x₁x₂)=х₁®х₂= Úх₂; дизъюнкцию f₁₄(x₁x₂)=х₁Úх₂.

Кроме этого, имеются другие функции, зависящие от двух переменных: f₁(x₁x₂)= – функция Пирса (Вебба) («стрелка Пирса»); f₂(x₁x₂)= – запрет х₂; f₄(x₁x₂)= – запрет х₁; f₆(x₁x₂)=x₁Åx₂ –сложение по модулю 2 (функция, инверсная эквиваленции); f₇(x₁x₂)= – функция Шеффера («штрих Шеффера»).

18 Определение свойств переключательных функций.