116

Основные понятия теории множеств

Понятия «множество», «элемент множества» - Под множеством понимают любое собрание определенных и различимых между собой объектов, мыслимых как единое целое. родоначальник современной теории множеств – немецкий математик Г. Кантору (1845-1918 гг.) собрание различных объектов рассматривается как один объект «множество», «быть элементом множества». Объекты, образующие множество, называют элементами множества и обозначают, как правило, строчными, а множества – прописными буквами латинского алфавита.

Для обозначения принадлежности элемента m множеству М будем использовать запись mÎМ,

Множество, содержащее конечное число элементов, называют конечным. Пустое множество, не содержащее ни одного элемента и обозначаемое символом Æ. Число элементов конечного множества М называют мощностью и обозначают |М|. Мощность бесконечного множества – более сложное понятие.

Каждое множество полностью задается своими элементами. Для этого можно перечислить элементы конечного множества или указать свойства элементов. Обычно для задания множеств используются фигурные скобки {}. Например:

А={a,b,c,d}

B={i:i – четное число}.

А – конечное множество, состоящее из четырех элементов a,b,c,d. В – бесконечное множество, заданное свойством элементов i, которое записывается справа от двоеточия. Одноместный предикат Р(i) («быть четным числом»). Множество может быть задано также некоторой порождающей процедурой - образование множеств из других множеств с помощью операций над множествами.

В множестве могут быть выделены подмножества. Если каждый элемент множества С принадлежит множеству D, то множество С называется подмножеством множества D. Это обозначается как СÍD (DÊС), где Í – знак включения

Говорят, что множества С и D находятся в отношении включения, а элементы множества к самому множеству – в отношении принадлежности.

Если АÍВ и А¹В, то А называют собственным,истинным подмножеством и обозначают АÌВ, где Ì – знак строгого включения.

Для каждого множества М существует множество, элементами которого являются все его подмножества. Такое множество называется булеаном множества и обозначается В(М), а множество М – универсумом (универсальным) и обозначается I [9-10].

Пусть I={a,b}, тогда B(I)={Æ,{a},{b},{а,b}}. Для I={a,b,с}, B(I)={Æ,{a},{b},{c},{а,b},{a,c},{b,c},{a,b,с}}.

Множества часто задают графически с помощью диаграмм Эйлера (рис. 1).

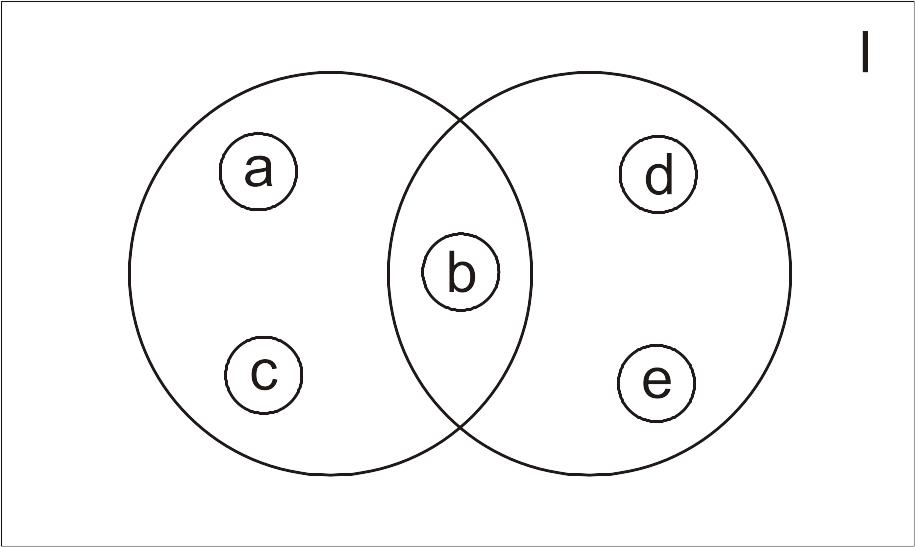
Рис. 1. Пример диаграммы Эйлера для множеств

{{а,b,с},{b,d,e}} в универсуме {а,b,с,d,e}

На рис. 1 заданы множества {{а,b,с},{b,d,e}} в универсуме I={а,b,с,d,e}, замкнутая линия, называемая кругом Эйлера, соответствует одному из рассматриваемых множеств и ограничивает его элементы, при этом рамка, в верхнем правом углу которой обозначено I, ограничивает элементы универсума (универсального множества).

1.2. Основные операции над множествами

Объединением АUВ, все элементы которого являются элементами множества А или множества В:

АUВ={x:xÎA или хÎВ},

где U – знак объединения.

На диаграмме Эйлера это может быть показано штриховкой (рис. 2).

Рис. 2. Объединение множеств АUВ

Пересечением АIВ, элементы которого являются элементами обоих множеств:

АIВ={x:xÎA и хÎВ},

где I – знак пересечения.

Соответствующая диаграмма Эйлера изображена на рис. 3.

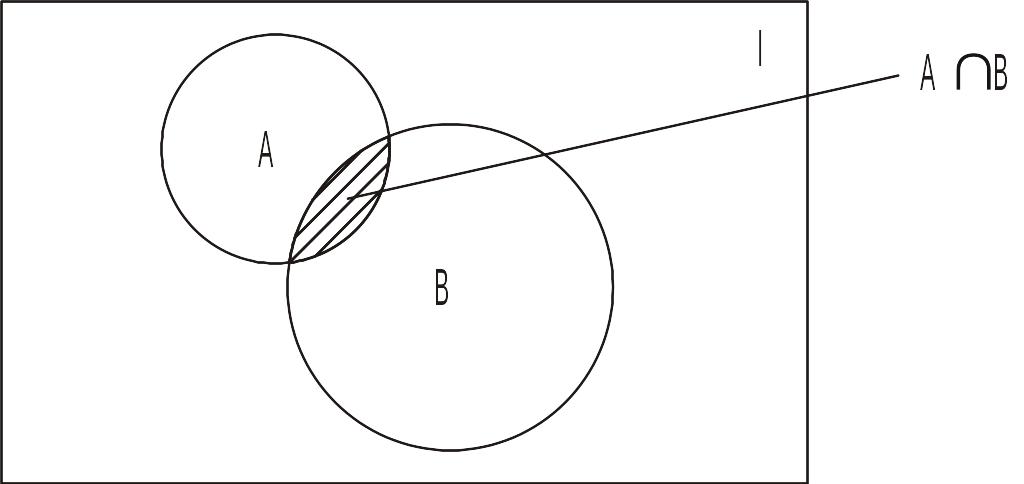
Рис. 3. Пересечение множеств АIВ

Разностью А\В, состоящее из элементов, принадлежащих множеству А и не принадлежащих множеству В:

А\В={x:xÎA и х В},

где – знак непринадлежности (отрицание принадлежности), \ – знак разности.

Соответствующая диаграмма Эйлера изображена на рис. 4.

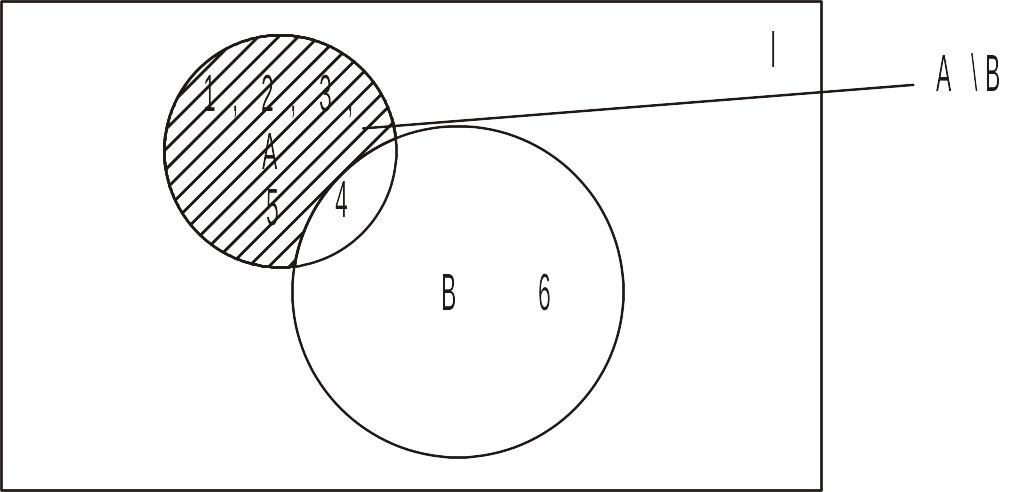
Рис. 4. Разность множеств А\В

Так, если А={1,2,3,4,5}, В={4,6}, то А\В={1,2,3,5}, В\А={6}.

Симметрической разностью АÅВ=(А\В)U(В\А), изображенное на рис. 5, Å – знак симметрической разности.

Так, если А={1,2,3}, В={3,4,5}, то АÅВ={1,2,4,5}.

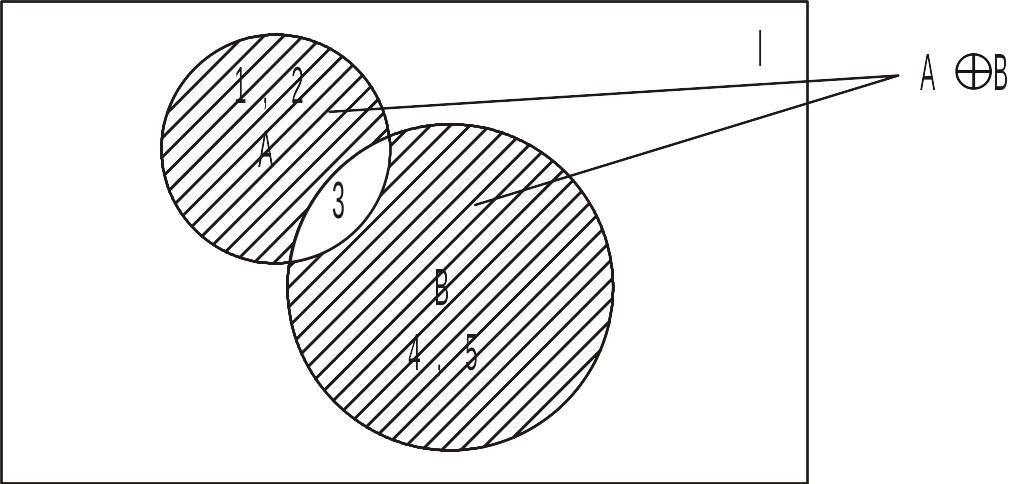
Рис. 5. Симметрическая разность множеств АÅВ

Рассмотренные операции являются двухместными (бинарными). Имеется одноместная (унарная) операция дополнения.

Дополнением , содержащее элементы универсума I, не включенные во множество А:

где – знак дополнения, «инверсия», читается «не А».

Соответствующая диаграмма Эйлера изображена на рис. 6.

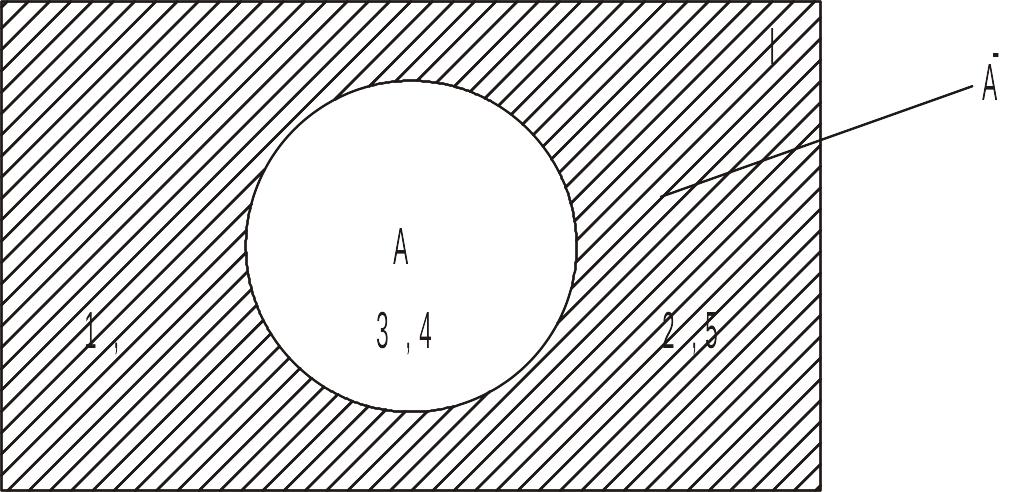
Рис. 6. Дополнение множества А до универсума I

Так, если А={3,4}, а I={1,2,3,4,5}, то`A={1,2,5}.

Используя рассмотренные операции, можно выражать одни множества через другие, при этом сначала выполняется одноместная операция дополнения, затем пересечения и только потом – операция объединения (разности). Для изменения порядка выполнения операций в выражении используют скобки.

2. Операции на множествах

Частным случаем функции является операция, F отображение вида j: MⁿaМ, где a знак отображения. Такая F называется n-арной операцией, в ней области определения аргументов и область значений функции совпадают, n-местная операция по n элементам множества определяет (n+1)-й элемент этого же множества [9-10].

Алгеброй А называется совокупность <> множества М с заданными на нем операциями S={j₁₁,j₁₂,...j_1n1,j₂₁,...j_2n2,j_m1,j_m2,...j_mnm}, А=<М,S>, где множество М – носитель, S – сигнатура алгебры [9-10, 19]. Каждый первый индекс у идентификатора операции указывает ее местность.

Алгебра типа <М,j₂>, т.е. алгебра с бинарной операцией, называется группоидом.

Рассмотрим квадрат с вершинами в точках а₁, а₂, а₃, а₄, пронумерованных против часовой стрелки, и повороты квадрата вокруг центра также против часовой стрелки, переводящие вершины в другие вершины [19]. Таких поворотов бесконечное множество: на углы 0, , p, 3 , 2p, 5 , ..., однако они задают всего четыре различных отображения множества вершин в себя, соответствующих первым четырем поворотам.

Можно сказать, что задана алгебра А=<М,j₁> с основным множеством М={а₁,а₂,а₃,а₄} и четырьмя унарными операциями МaМ, которые обозначим буквами a, b, n, d. Зададим эти операции таблицей (табл. 1).

Таблица 1

Унарные операции алгебры поворотов квадрата

	a	b	n	d
а1	а1	а2	а3	а4
а2	а2	а3	а4	а1
а3	а3	а4	а1	а2
а4	а4	а1	а2	а3
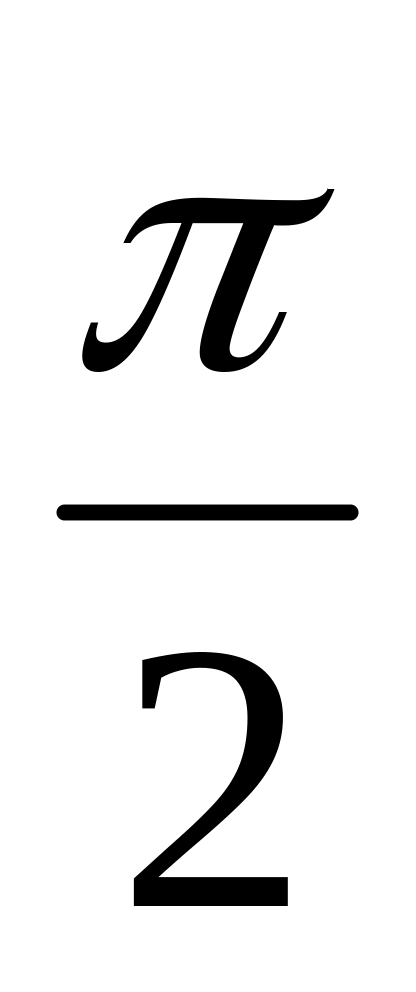
	0		p	3

Можно интерпретировать такие операции также циклическими сдвигами бит информации вида:

.

Множество 0={a,b,n,d} отображений вершин в себя вместе с бинарной операцией 0²a0 последовательного выполнения отображений (выполнения поворота за поворотом, композиции поворотов), которую обозначим символом «¤» образует алгебру с бинарной операцией <0, ¤> [19]. Она задается табл. 2, в которой на пересечении строки i и столбца j записан результат операции ioj.

Таблица 2

Бинарные операции 0²a0 алгебры

композиций поворотов квадрата

i j	a	b	n	d
a	a	b	n	d
b	b	n	d	a
n	n	d	a	b
d	d	a	b	n	I¤j

Такая таблица (см. табл. 2), задающая бинарную операцию, называется таблицей Кэли.

Можно представить бинарной операцией, например, смешивание красок, когда из двух цветов получается третий, входящий, однако во множество всех цветов.

Пусть А=<М,j₂> – группоид. Обозначим, как и в предыдущем примере, j₂ символом ¤ [9].

Тогда элемент nÎМ называется правым нейтральным элементом группоида А, если для всякого mÎМ выполняется равенство m¤n=m.

Для левого нейтрального элемента выполняется равенство n¤m=m.

В дальнейшем для краткости вместо слов «все», «всякий» будем использовать символ " (перевернутая буква А – первая буква английского слова All – все, этот символ называется еще квантором общности; квантор существования обозначается $ и означает «существует», «имеется», «есть»).

Элемент n, являющийся одновременно и левым, и правым нейтральным элементом, называют двухсторонним нейтральным элементом или просто нейтральным элементом.

Для смешивания красок нейтральный элемент – бесцветный лак.

Если группоид <М, ¤> мультипликативный, т.е. его бинарная операция ¤ имеет тип умножения (·), то нейтральный элемент называется единицей и обозначается 1, если группоид аддитивный, т.е. бинарная операция ¤ имеет тип сложения (+), то нейтральный элемент называется нулем и обозначается 0 [9]. Нейтральный элемент в группоиде всегда единственный.

Коммутативный группоид, т.е. группоид, в котором

("х,yÎМ)(х¤y=y¤х),

называется коммутативным или абелевым.

Группоид, в котором выполняется закон ассоциативности

("х,y,zÎМ)(х¤ (y¤z)=(x¤y) ¤z),

называется ассоциативным или полугруппой.

Полугруппа с единицей называется моноидом. В алгебре поворотов квадрата (см. табл. 2) единицей служит поворот на нулевой угол (a).

Группой называется полугруппа с единицей, в которой для каждого элемента а существует элемент а^-1, называемый обратным (а¤а^-1=а^-1¤а=n) и каждое из уравнений a¤x=b, y¤a=b обладает единственным решением [9].

В алгебре поворотов квадрата (см. табл. 2), являющейся группой, обратным к данному повороту является поворот, дополняющий его до 2p:

b^-1=d, n^-1=n, d^-1=b.

Группа, все элементы которой являются степенями одного элемента а, называется циклической. Циклическая группа всегда абелева.

Множество рациональных чисел, не содержащее нуля, с операцией умножения является абелевой группой. Обратным к элементу а, является элемент .