8.2. Основные понятия и определения, используемые при минимизации

При минимизации переключательных функций существенную роль играют понятия импликанты, простой импликанты, имплиценты и простой имплиценты [14]. Пусть f(x), g(x), p(x) – полностью определенные функции, причем под х понимается некоторый набор из n переменных (х₁х₂...х_n). Функция f(х) определена на рабочих (единичных) наборах М₁[f(х)] и множестве запрещенных (нулевых) наборов М₀[f(х)]. Функция g(x) определена на множестве рабочих (единичных) наборов М₁[g(x)], а функция р(х) – на множестве запрещенных (нулевых) наборов М₀[р(х)].

Переключательная функция g(х) называется импликантой переключательной функции f(х), если множество рабочих (единичных) наборов функции g(х) совпадает или является подмножеством множества рабочих наборов функции f(х), т.е. М₁[g(x)]Í М₁[f(x)], где Í – знак включения в множество, означающий, что всякий элемент левого множества является элементом правого множества. При этом говорят, что М₁[f(x)] содержит М₁[g(x)], т.е. в соответствии с определением импликации g(x)®f(x).

Переключательная функция р(х) является имплицентой переключательной функции f(х), если множество запрещенных (нулевых) наборов функции р(х) совпадает или является подмножеством множества запрещенных (нулевых) наборов функции f(х), т.е. М₀[р(x)]Í М₀[f(x)].

Пусть функция в СДНФ имеет вид:

f(x₁x₂x₃)=`x<sub>1</sub> x<sub>2</sub> x<sub>3</sub> Ú x<sub>1</sub> x<sub>2</sub>`x₃ Ú x₁x₂x₃;

g₁(x)=`x₁ x₂ x₃ (конституента СДНФ);

g₂(x)= х₁ х₂`x₃ (конституента СДНФ);

g₃(x)= х₁ х₂ х₃ (конституента СДНФ);

g₄(x)= f(х), т.е. сама функция в СДНФ.

Из СДНФ можно получить другие импликанты путем всевозможных группировок ее членов и многократного использования (по возможности) закона склеивания, пока не останется конъюнкций, отличающихся значениями одной переменной ( в одной, в другой, если остальные члены конъюнкции одинаковы).

Так:

Группировка первой и второй конституенты не позволяет применить закон склеивания:

Других вариантов комбинаций и склеиваний для f(х) нет.

Простой импликантой функции f(х) называется любая элементарная конъюнкция в g(х), являющаяся импликантой функции и обладающая тем свойством, что никакая ее собственная часть уже не является импликантой. В примере импликанты g₅=х₁х₂, g₆=х₂х₃ являются простыми импликантами функции f. Импликанты g₁, g₂, g₃, g₇ и, естественно, g₄ – не являются простыми, т.к. их части являются импликантами функции f: например, g₅ является частью g₂ (g₃). Говорят, что простые импликанты покрывают или поглощают соответствующие конституенты.

В булевой алгебре переключательных функций утверждается и доказывается: 1) дизъюнкция любого числа импликант переключательной функции также является импликантой этой функции; 2) любая переключательная функция равносильна дизъюнкции всех своих простых импликант, и такая форма ее представления называется сокращенной ДНФ (СкДНФ). Рассмотренный перебор всех возможных импликант переключательной функции f дает возможность убедиться, что простых импликант всего две: g₅, g₆. Тогда сокращенная ДНФ функции f имеет вид:

f=g₅Úg₆=х₁х₂Úх₂х₃.

Рабочими наборами функции f(х₁х₂х₃) являются 011, 110, 111 (табл. 34). Из таблицы видно, что импликанты g₅, g₆ в совокупности покрывают своими единицами все единицы функции f, т.е. рабочие наборы сокращенной ДНФ = 110, 111, 011, 111, последний повторяется дважды. Получение сокращенной ДНФ – первый этап минимизации.

Иногда из сокращенной ДНФ можно убрать одну или несколько простых импликант, не нарушая количества необходимых рабочих наборов. Такие простые импликанты назовем лишними. В нашем случае их нет. Исключение лишних простых импликант из сокращенной ДНФ – второй этап минимизации.

Таблица 34

Таблица истинности импликант

				Импликанты
х1	х2	х3	f	g1	g2	g3	g4=f	g5	g6	g7
0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0
0	1	1	1	1	0	0	1	0	1	1
1	0	0	0	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0	0	0	0
1	1	0	1	0	1	0	1	1	0	1
1	1	1	1	0	0	1	1	1	1	0

Сокращенная ДНФ переключательной функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.

Устранение лишних простых импликант из сокращенной ДНФ переключательной функции не является однозначным процессом, т.е. переключательная функция может иметь несколько тупиковых ДНФ.

Тупиковые ДНФ, содержащие минимальное число букв, являются минимальными.

Минимальных ДНФ тоже может быть несколько. Минимальная ДНФ функции, найденная путем построения и перебора всех тупиковых ДНФ и выбора из них самой минимальной, называется общей (абсолютной) тупиковой ДНФ.

Поиск минимальной ДНФ всегда связан с перебором решений. Существуют методы уменьшения перебора, но он всегда имеется. Как правило, ограничиваются нахождением одной или нескольких тупиковых ДНФ, из которых выбирают минимальную, – её называют частной минимальной ДНФ и считают близкой к общей (абсолютной).

При минимизации не полностью определенных переключательных функций особенностью является то, что необходимо найти такое ее доопределение за счет условных наборов, которое соответствует минимальной ДНФ, содержащей наименьшее число букв.

22.Метод Квайна.

Метод основан на попарном сравнении и склеивании при возможности всех конституент (членов СДНФ). Для этого каждая конституента сравнивается с последующими, что приводит к получению импликант. Полученные импликанты вновь подвергаются сравнению и при возможности склеиваются – и т.д. до тех пор, пока оставшиеся импликанты уже не будут поддаваться склеиванию. Это и есть простые импликанты, их дизъюнкция представляет собой сокращенную ДНФ.

Для упорядочения целесообразно разбивать конституенты на группы по числу неинверсированных переменных. В этом случае каждая очередная конституента, начиная сверху, сравнивается только с конституентами группы, соседней снизу, с числом неинверсированных переменных на единицу больше.

Пусть имеется переключательная функция, заданная СДНФ:

Разобьем конституенты на группы по числу неинверсированных переменных.

Римская цифра номера группы соответствует числу неинверсных переменных. Проведем линии, указывающие склеиваемые конституенты. Результатом склеивания является всегда элементарная конъюнкция, представляющая собой общую часть исходных конъюнкций (в частности, конституент).

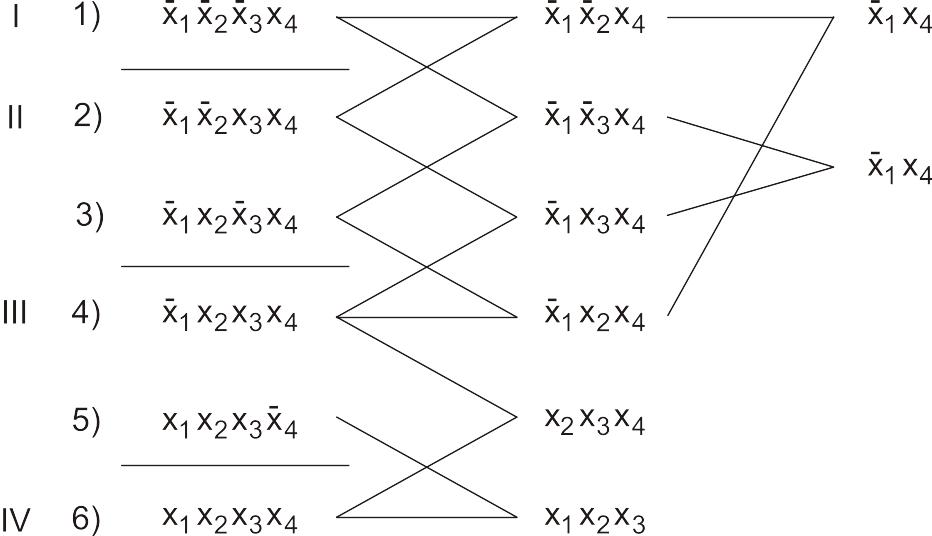
Полученные импликанты также допускают склеивание, причем в результате получается одна и та же импликанта .

Дальнейшие склеивания невозможны, поэтому полученные импликанты – простые, а сокращенная ДНФ имеет вид:

Первый этап выполнен. На втором этапе необходимо исключить лишние простые импликанты. Это делается с помощью специальной импликантной таблицы Квайна (таблицы покрытий). Строки таблицы отмечаются простыми импликантами переключательной функции, т.е. членами сокращенной ДНФ, а столбцы – конституентами единицы, т.е. членами СДНФ переключательной функции.

Как уже отмечалось, простая импликанта поглощает некоторую конституенту единицы, если является ее собственной частью. Соответствующая клетка импликантной таблицы на пересечении строки данной простой импликанты и столбцов с конституентами единицы отмечается, например, знаком «+». Минимальные ДНФ строятся по импликантной таблице следующим образом:

1) ищутся столбцы импликантной таблицы, имеющие только один крестик, соответствующие этим крестикам простые импликанты называются базисными и составляют так называемое ядро переключательной функции. Ядро обязательно входит в минимальную ДНФ;

2) рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы импликантной матрицы, и выбираются варианты с минимальным суммарным числом букв.

Ядром нашей функции (табл. 35) являются импликанты и х₁х₂х₃, т.е. функция имеет единственную тупиковую и минимальную ДНФ:

Таблица 35

Импликантная таблица Квайна

	Простые	Конституенты 1 (члены СДНФ)
	импли-канты
А		+	+	+	+
В	х2х3х4				+		+
С	х1х2х3					+	+

Видно, что импликанта х₂х₃х₄ является лишней, так как она покрывает конституенты, уже покрытые импликантами , х₁х₂х₃.

Число крестиков в строке является степенью числа 2; более того, можно убедиться, что оно равно N=2^n-k, где k – число букв в простой импликанте, n – число переменных, от которых зависит функция.

Если вначале не задана СДНФ, то ее надо получить, используя, например, уже известные нам методы.

Ясно, что для больших импликантных таблиц трудно визуально выявить варианты с минимальным числом букв. Поэтому используется метод Петрика, позволяющий получать все тупиковые ДНФ по импликантной таблице путем построения так называемого конъюнктивного ее представления. Для этого все простые импликанты обозначаются разными буквами (А, В, С в табл. 35), а затем для каждого столбца строится дизъюнкция всех букв, обозначающих строки таблицы, пересечение которых с данным столбцом отмечено крестиком. Конъюнктивное представление импликантной матрицы образуется как конъюнкция построенных дизъюнкций для всех столбцов. К конъюнктивному представлению импликантной таблицы могут быть применены все соотношения булевой алгебры переключательных функций с целью его упрощения. После раскрытия скобок и выполнения всех возможных поглощений получается дизъюнкция конъюнкций, каждая из которых содержит все импликанты тупиковой ДНФ.

Это означает, что тупиковая ДНФ содержит две простые импликанты ( и одновременно С=х₁х₂х₃) и имеет вид:

Метод Квайна-Мак-Класки.

Метод представляет собой формализацию метода Квайна, ориентированную на использование ЭВМ. Формализация заключается в записи конституент единицы (членов СДНФ) их двоичными номерами. Все номера разбиваются на непересекающиеся группы по числу единиц в двоичном номере. Склеивания производятся только между соседними группами. Ликвидируемый разряд обозначается знаком «–» («тире»). Дальнейшие группы из полученных импликант образуются с учетом однинакового расположения тире. Такое обозначение импликант называется обобщенными кодами. Пусть задана логическая функция

®111Ú101Ú001Ú000Ú110.

Сгруппируем эти конституенты единицы по числу единиц:

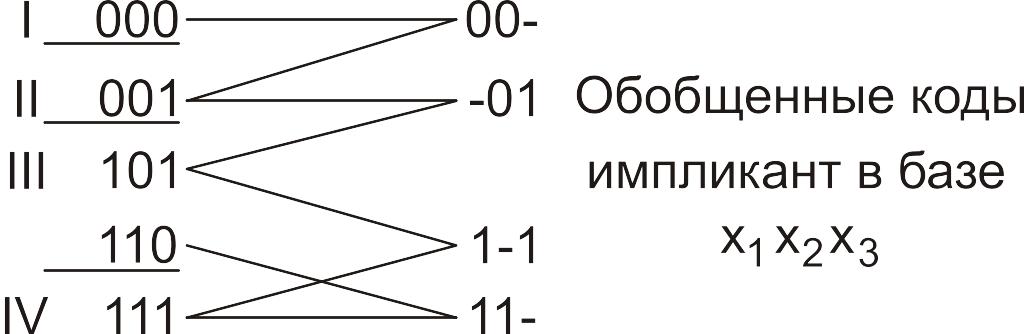
Дальнейшие склеивания невозможны. Нахождение минимальных ДНФ далее производится по импликантной таблице (табл. 36):

Это означает, что тупиковые ДНФ содержат по три простые импликанты и имеют вид:

(две инверсии);

(три инверсии).

Таблица 36

Импликантная таблица Квайна-Мак-Класки

	Простые импликанты			Конституенты единиц
	х1	х2	х3	111	101	001	000	110
А	0	0	-			+	+
В	-	0	1		+	+
С	1	-	1	+	+
D	1	1	-	+				+

Заметим, что склеивание двух импликант с тире возможно только при соответствующем их расположении, например:

00-- 01--
1-01 0101

Можно выбрать любую из полученных ТДНФ, а с учетом меньшего числа инверсий – первую.

23 Минимизация переключательных функций по картам Карно

При решении задач минимизации как полностью определенных, так и не полностью определенных переключательных функций, зависящих от небольшого числа переменных, широкое применение находят графические методы. Чаще всего эти методы применяются для минимизации переключательных функций четырех переменных, однако при соответствующем навыке их можно применять и для функций пяти-шести переменных. При большом числе переменных графические методы теряют свое основное достоинство – наглядность.

Метод минимизации по картам Карно позволяет графически получать экономное покрытие переключательной функции правильными конфигурациями её единиц. Карта Карно – это таблица истинности специального вида, в которой переменные функции расположены не одномерным, а двумерным массивом (по горизонтали и вертикали), причем каждому набору переменных поставлена в соответствие одна клетка. В эту клетку записывается значение функции (0 или 1) на данном наборе. Входные переменные располагаются по внешним сторонам карты напротив её строк и столбцов. При этом единичное значение переменной традиционно обозначается скобкой или линией «влияния» на строки или столбцы, для остальных строк (столбцов) значение этой переменной равно нулю.

Каждая из входных переменных делит карту Карно на две разные части, в одной из которых значение этой переменной равно 1, а в другой 0.

Каждой клетке карты Карно соответствует один определенный набор, а каждая сторона клетки представляет собой границу между значениями переменных. Карты Карно для одной и двух переменных изображены на рис. 41.

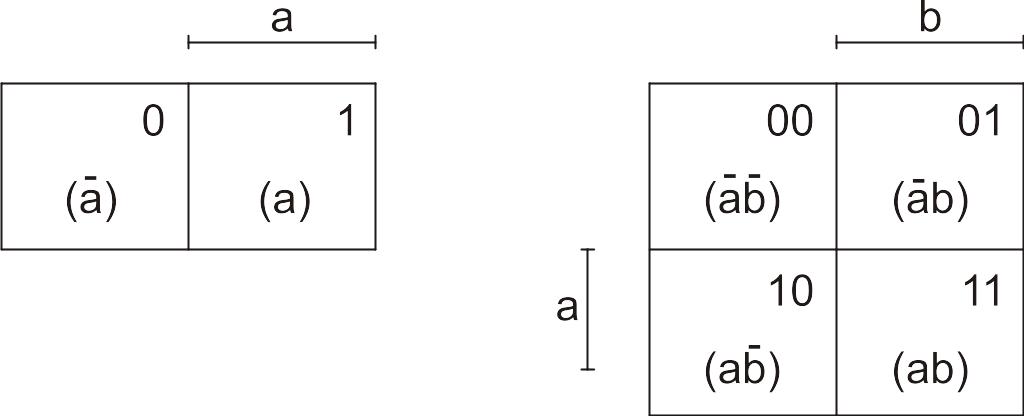
Рис. 41. Карты Карно для одной и двух переменных

В правом углу для пояснения указаны наборы переменных, соответствующих клеткам, в базе переменных «аb» («а» имеет вес 2¹, «b» –2⁰).

Задание переключательных функций картами Карно является более компактным, а самое главное – более наглядным, с точки зрения визуального выделения групп рабочих (единичных) наборов. Число клеток карты Карно равно числу таблицы истинности, т.е. 2ⁿ, где n – число входных переменных. В каждой новой переменной число клеток удваивается, т.е. карта увеличивается вдвое.

Пусть задана таблица истинности функции 3-х аргументов, равная единице тогда, когда две входных переменных равны единице (две и только две!). Это так называемая мажоритарная функция или функция голосования по большинству «2 из 3-х» (табл. 38).

Таблица 38

Мажоритарная функция

Входной набор			z
а	b	с
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Представим эту функцию в виде карты Карно (рис. 42).

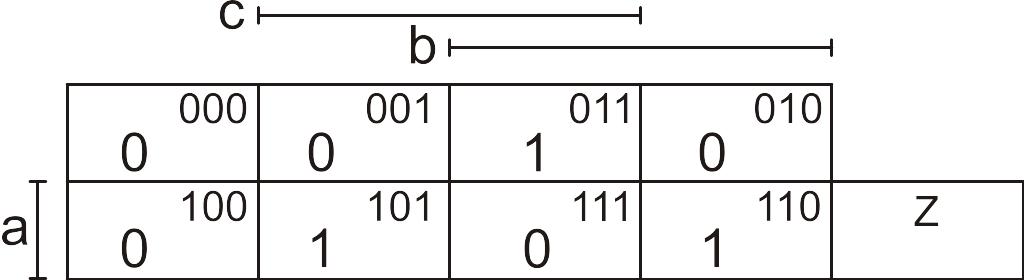
Рис. 42. Задание мажоритарной функции картой Карно

Если функция задана СДНФ, её также просто представить в виде карты Карно. Если функция задана в ДНФ, то необходимо проставить единицы в те клетки, которые соответствуют областям конъюнкции соответствующих переменных. Пусть задана та же функция «голосование по большинству голосов» («2 из 3-х» или мажоритарная функция): f(аbс)=аb Ú bс Ú ас.

Тогда в карте Карно на три переменных единицы проставляются в клетках, соответствующих пересечению «областей влияния» одновременно двух переменных: а и b, b и с, а и с (рис. 43).

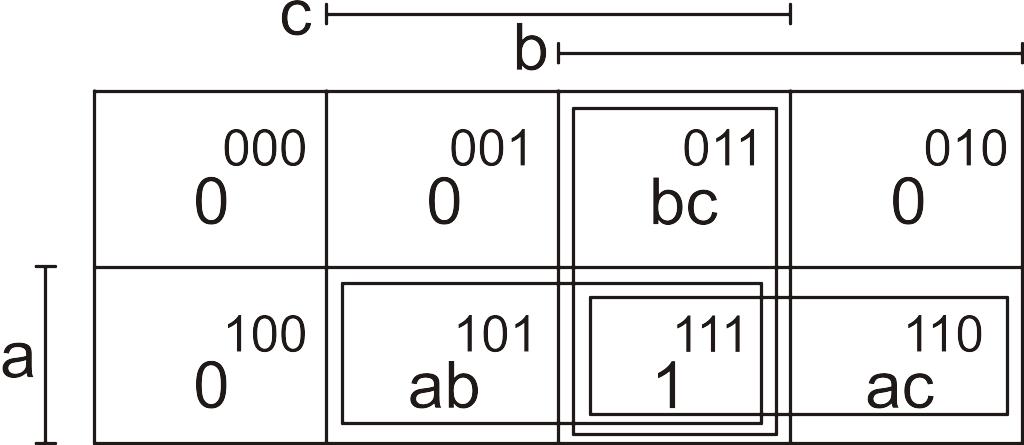
Рис. 43. Задание картой Карно f(аbс)=аb Ú bс Ú ас

Можно получить СДНФ, рабочие наборы этой функции:

.

Аналогично может быть получена СКНФ функции:

.

Для неполностью определенной переключательной функции проставляются знаки «~» («тильда») в клетках, соответствующих условным наборам.

Карта Карно на четыре переменных содержит 16 клеток (рис. 44).

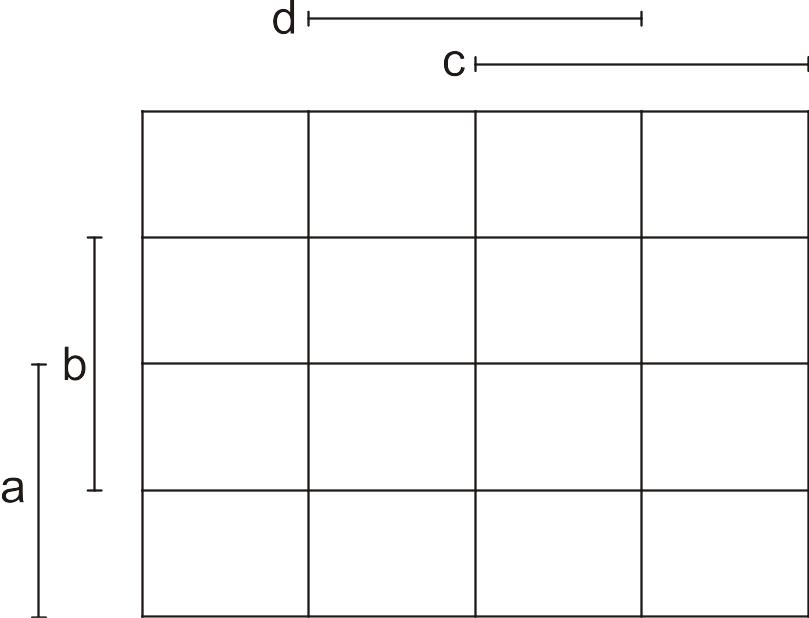
Рис. 44. Карта Карно на четыре переменных

Такая таблица гораздо компактней, чем таблица истинности из 16 строк. Заметим, что переменные в карте Карно проставляются в определенном порядке так, чтобы каждая покрывала половину карты и не повторяла других переменных. Переменные базы в карте Карно 4-х переменных следуют: по вертикали – снизу вверх, по горизонтали – справа налево (кстати, карты Карно и подобные им карты Вейча отличаются способом кодировки – вариантами проставления переменных).

Карты Карно имеют замечательное свойство, заключающееся в том, что наборы значений переменных для клеток, стоящих рядом (соседние клетки), отличаются значением лишь одной переменной. При переходе от одной клетки в соседнюю, всегда изменяется значение лишь одной переменной («1» на «0» или наоборот).

Так для карты четырех переменных (рис. 44) для второго столбца и третьей строки получаются следующие конституенты или наборы переменных номера клетки (рис. 45).

Очевидно, что наборы переменных (соответствующие конституентам переключательной функции) двух соседних клеток отличаются друг от друга значением только одной переменной. Такие наборы, отличающиеся значением одной переменной, называются соседними наборами (кодами). Таким образом, соседние клетки карты Карно имеют соседние коды (наборы). Можно также сказать, что между соседними кодами имеется кодовое расстояние, равное единице (кодовое расстояние равно количеству разрядов, в которых коды отличаются друг от друга). Соседними являются также крайние левые клетки карты Карно с крайними правыми клетками и крайние верхние клетки с крайними нижними (как если бы карта была свернута по вертикали и по горизонтали). В этом легко убедиться, сравнивая наборы (рис. 45).

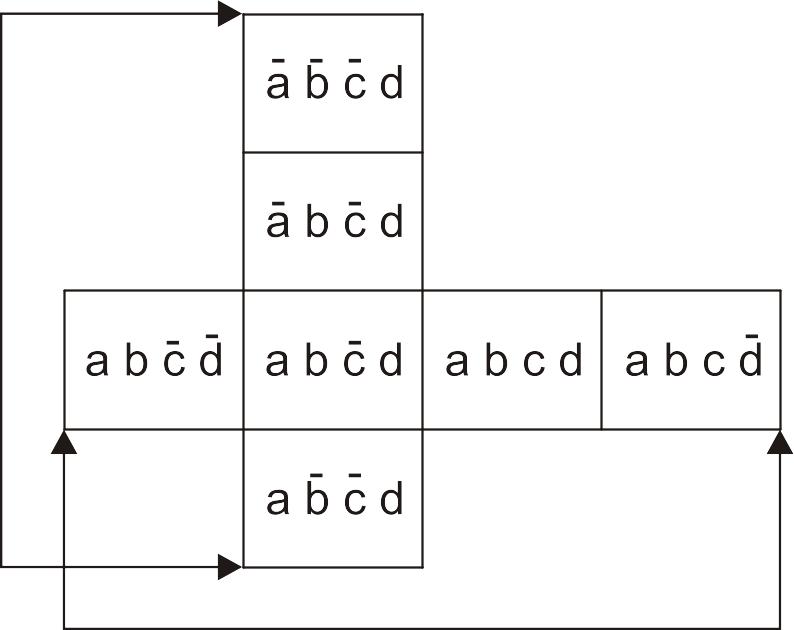
Рис. 45. Иллюстрация соседних клеток карты Карно

(соседние по переменной а),

(соседние по переменной с).

На картах Карно до 4-х переменных соседние клетки расположены рядом, граничат друг с другом, т.е. соседство очевидно.

На картах Карно пяти и более переменных, соседние клетки, отличающиеся значением только одной переменной, не всегда расположены рядом, т.е. их соседство не очевидно. Поэтому чаще всего минимизиция по картам Карно используется для функций, зависящих не более чем от четырех переменных.

Минимизация переключательной функции по карте Карно в классе ДНФ заключается в покрытии ее единиц минимальным количеством максимальных правильных контуров. В эти контуры могут включаться и условные наборы. Контуры могут пересекаться, но не могут включаться друг в друга – иначе не получатся простые импликанты. Правильными контурами для карты 4-х переменных могут быть следующие:

одноклеточный – одна клетка с единицей, окруженная нулями;

двухклеточный – две соседние клетки, окруженные нулями;

четырехклеточный – квадрат из четырех соседних клеток, окруженных нулями;

восьмиклеточный – куб из восьми соседних клеток, окруженных нулями;

сверхкуб (гиперкуб) – соответствует вырожденной функции четырех переменных, не зависящей от переменных – нет ни одного нуля. Он используется для функций пяти и более переменных.

Типичные конфигурации максимальных правильных контуров представлены: на рис. 46-48 [17].

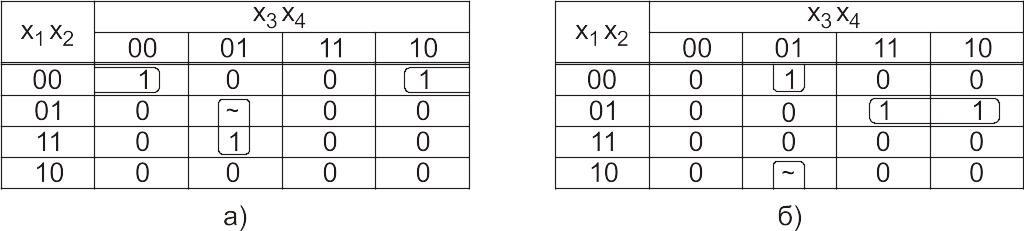
Рис. 46. Двухклеточные

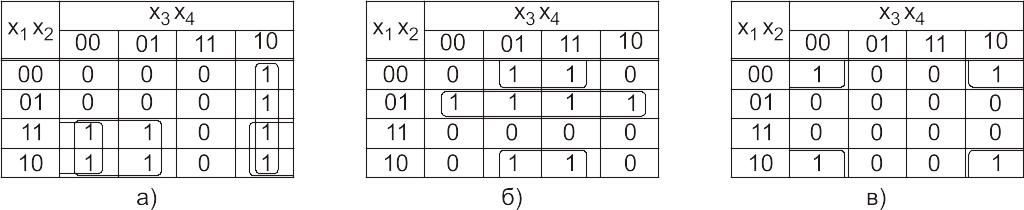
Рис. 47. Четырехклеточные

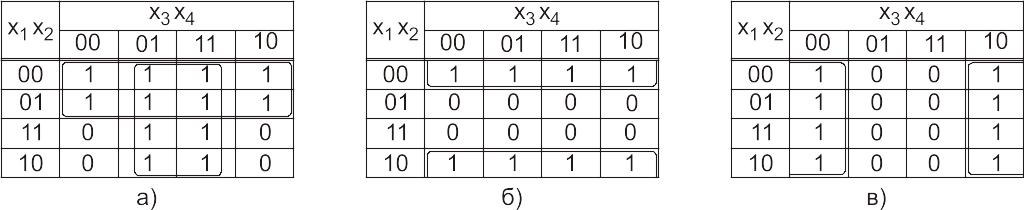
Рис. 48. Восьмиклеточные

На этих рисунках изображена так называемая цифровая кодировка карт. Особое внимание следует обращать на контуры, которые имеют видимый разрыв, так как объединяемые ими соседние клетки находятся в крайних строках или столбцах карты Карно. Найдем импликанты соответствующих функций для рис. 46а. Воспользуемся методом Квайна-Мак-Класки: f(х₁х₂х₃х₄)=0000Ú0010Ú0101Ú1101. Ясно, что наборы 0000 и 0010 склеиваются по переменным х₁х₂х₄ (00-0), а наборы 0101 и 1101 – по переменным х₂х₃х₄ (-101). Получаем две импликанты:

Однако нет необходимости производить склеивания – нетрудно убедиться, что простая импликанта легко находится по карте следующим образом: в нее входят те переменные, которые во всех клетках данного контура не меняют своего значения (речь идет о номере клетки!). Для рис. 46б получаем:

Для рис. 47а:

Для рис. 47б:

Для рис. 47в:

Для рис. 48а:

Для рис. 48б:

Для рис. 48в:

По карте Карно удобна также минимизация в классе КНФ. В этом случае каждому контуру из нулей с возможным добавлением «тильд» соответствует имплицента – член КНФ, которая строится также из переменных, не меняющих своего значения в номере клеток «нулевого» контура, только, если переменная в номере клетки равна нулю, то в КНФ она будет без инверсии, а если равна единице – то в КНФ она будет с инверсией.

Так, для рис. 46б f(х₁х₂х₃х₄) получим имплиценты:

1) (х₂Ú х₄) – угловые клетки;

2) – квадрат (0100,1100,0101,1101);

3) – квадрат (1111,1110,1011,1010);

4) – квадрат (0011,0010,1011,1010).

Таким образом:

24 Метод поразрядного сравнения рабочих и запрещенных наборов

Несложные функции удобно минимизировать путем сравнения рабочих и запрещенных наборов. Задача заключается в том, чтобы в каждом рабочем наборе оставить минимальное количество переменных, позволяющих отличить этот набор от всех запрещенных наборов.

Покажем это на примере минимизации функции «импликация х в y»:

х

у

(0)	0
(0)	1
1	(1)

1

0

Здесь отдельно записаны три рабочих (единичных) набора: 00, 01, 11. Набор 10 запрещенный (нулевой). Видно, что в наборе 00 достаточно оставить переменную x, поскольку значение этой переменной в одном – единственном запрещенном наборе равно 1. Таким образом, получили импликанту (0-). Эта же импликанта покрывает и набор 01. Тогда для набора 11 необходимо оставить переменную y, то есть, получили импликанту (-1). Таким образом, импликация представлена в виде (0-)Ú(-1), то есть x®y =`xÚy.

Часто такую минимизацию удобно выполнять графически, например, на кубе соседних чисел, и объединять рабочие вершины в фигуры, покрываемые одной импликантой. Для функции трех переменных возможны следующие фигуры: вершина, ребро, сторона.

Пример минимизации двоичной переключательной функции, заданной своим десятичным номером по решетке Хассе (кубу соседних чисел).

Дано: двоичная переключательная функция (ПФ) №174₁₀ (табл. 39).

Получим соответствующий двоичный код: 10101110₂ (2⁷+2⁵+2³+2²+2¹).

Таблица 39

Таблица истинности ПФ №174₁₀

Переменные			ВС	f(abc)
а	b	с
0	0	0	0	0	20
0	0	1	1	1	21
0	1	0	2	1	22
0	1	1	3	1	23
1	0	0	4	0	24
1	0	1	5	1	25
1	1	0	6	0	26
1	1	1	7	1	27

Минимизируем ПФ по кубу соседних чисел (рис. 49, рабочие вершины закрашены):

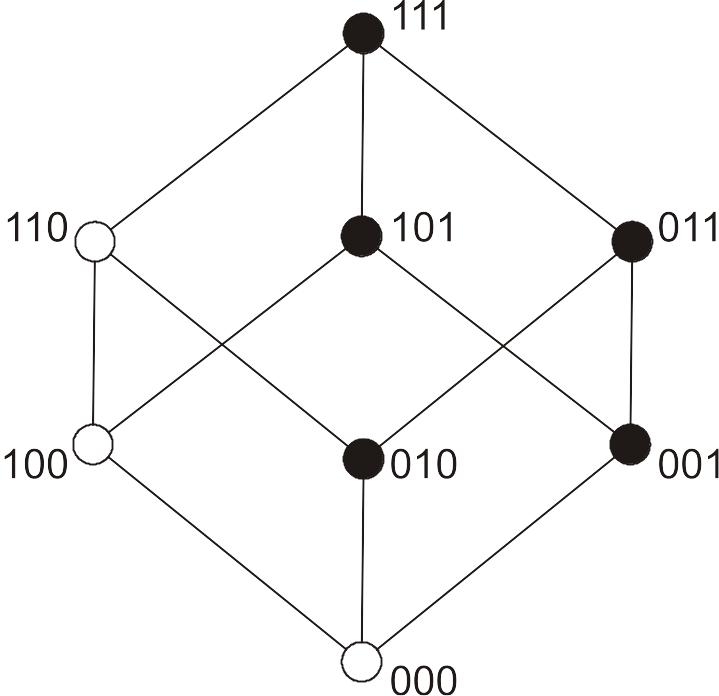
Рис. 49. Минимизация ПФ №174₁₀ по решетке Хассэ

Квадрат соответствует обобщенному коду – импликанте (--1).

Ребро соответствует обобщенному коду – импликанте (01–)

Таким образом, ДНФ ПФ имеет вид: , т.е f(abc)=c Ú`a b.

На использовании куба соседних чисел основан метод поразрядного сравнения рабочих и запрещенных восьмеричных наборов – метод Л.Ф. Викентьева [6, 17].

25 Минимизация переключательных функций на основе поразрядного сравнения рабочих и запрещенных восьмеричных наборов.

Основа метода заключается в том, что минимизация переключательной функции большого числа переменных сводится к минимизации нескольких переключательных функций, зависящих не более чем от трех переменных. В свою очередь, для упрощения эти отдельные функции минимизируются по кубу соседних чисел, то есть исходную функцию необходимо задать в символической форме в восьмеричной системе счисления.

Тогда для каждого разряда восьмеричного рабочего числа функции определяются запрещенные цифры, то есть такие, которые в совокупности с другими разрядами восьмеричного рабочего числа приведут к получению запрещенных чисел функции. Затем, используя куб соседних чисел, следует минимизировать функцию трех переменных (определить покрытие данного разряда). Так минимизируются все разряды. По полученным обобщенным кодам для каждого восьмеричного разряда определяется ДНФ для всего рабочего числа. По полученному покрытию определяют, какие рабочие числа покрывает дополнительно полученная импликанта (кроме данного числа). Числа, покрытые полученной импликантой, удаляют. Оставшиеся числа вновь подвергают минимизации – пока не будут покрыты все рабочие наборы. Метод особенно эффективен для недоопределенных функций.

Пример 1. Задана функция в восьмеричной системе счисления:

f₈(х₆х₅х₄х₃х₂х₁)=56[26].

Всего существует 64 набора переменных для функции 6 переменных. Как видно, используется только один рабочий и один запрещенный, остальные наборы – условные.

Каждое рабочее число соответствует члену СДНФ. Восьмеричная система позволяет очень легко переходить к СДНФ. Каждый разряд восьмеричного числа – это 3 разряда двоичного числа. В данном примере 6 переменных:

f₈ (х₆х₅х₄х₃х₂х₁)=(101110)= .

Таким образом, говорят, что ранг такого представления =6.

Определим запрещенные числа для старшего разряда числа 56, т.е. для 5. Будем подставлять вместо первого разряда возможные числа, а их всего 7 – система-то восьмеричная!

Получаем: 06,16,26,36,46,66,76. Видим, что число 2 – запрещенное, в совокупности с ним второй разряд (6) приводит к получению запрещенного набора 26.

Результат анализа запишем следующим образом:

Цифра 5, стоящая над чертой указывает заданное значение старшего разряда рабочего числа, а цифра 2, стоящая под чертой, – запрещенное значение этого разряда.

Минимизируем функцию трех переменных f₈ (х₆х₅х₄)= 5[2] по кубу соседних чисел (рис. 49). Получаем возможное покрытие (1Ú3Ú5Ú7) и импликанту (--1).

Запишем это таким образом:

Эта запись означает, что функцию, заданную одним рабочим числом 56, мы доопределили до четырех рабочих чисел: 16, 36, 56, 76. Число 56 – рабочее – вошло в покрытие, а вот запрещенное – 26 – нет.

Теперь нужно аналогичным образом минимизировать младший разряд рабочего числа. Определим возможные наборы, которые могут получиться путем соединения покрытия (1Ú3Ú5Ú7) и второго разряда, который может принимать значения 0,…,7: 10,…,17,30,…,37,50,…,57,70,…,77. Очевидно, что ни в одном случае мы не получим запрещенного набора 26, а значит, запрещенных чисел для второго разряда 6 рабочего числа 56 нет, поскольку запрещенный набор начинается на число 2, а двойки в покрытии (1Ú3Ú5Ú7) нет.

Запишем результат следующим образом:

где _.

Здесь прочерк под цифрой 6 означает отсутствие запрещенных разрядов.

Таким образом, доопределили функцию до 32 наборов, но набор 26, естественно, не вошел в покрытие. Пользуясь кубом соседних чисел, минимизируем второй разряд: f₈(х₃х₂х₁)=6.

Здесь нет запрещенных чисел, поэтому получаем импликанту (---), которая соответствует объединению всех вершин куба (полный куб): f₈(х₃х₂х₁)=(---).

Тогда f₈(х₆х₅х₄х₃ х₂х₁)=(--1)(---)=х₁.

Получено одно из возможных решений, представляющее собой простую импликанту переключательной функции, покрывающую рассмотренное восьмеричное рабочее число.

Минимизация методом поразрядного сравнения не однозначна, возможны различные варианты решений. Можно было при минимизации первого разряда взять другие квадраты (4Ú5Ú6Ú7), (0Ú1Ú4Ú5), тогда ответ был бы другим, но все равно ранг его был бы равен 1.

Пример 2. Минимизировать переключательную функцию, заданную в символической форме в восьмеричной системе счисления:

f₈(х₅х₄х₃ х₂х₁)=37,22,31[00,16,10].

Минимизируем рабочее число 37:

Проверим, какие рабочие числа покрывают этот член ДНФ (простая импликанта). Из выражения видно, что покрываются рабочие числа 37 и 31. Осталось число 22. Рассмотрим его:

Итак, f₈(х₅х₄х₃х₂х₁)=(--)(--1)Ú(--)(01-)= .

Здесь в первом разряде обобщенных кодов два (символов «тире»), т.к. функция зависит от пяти переменных. Говорят, что старшая триада неполная.

Теперь начнем минимизацию той же функции с младшего разряда:

Получили x₅. Очевидно, x₅ покрывает все рабочие числа 37, 22, 31.

Видим, что данный вариант дает самую минимальную форму.

26 Основные определения теории конечных автоматов

Конечным автоматом (просто автоматом) называется система (пятерка) [19]:

S=<X,Y,Z,j,y>,

в которой Х={х₁,х₂,...,х_i} – конечное входное множество (входной алфавит); Y={y₁,y₂,...,y_j} – конечное множество внутренних состояний автомата (алфавит состояний); Z={z₁,z₂,...,z_k} – конечное выходное множество (выходной алфавит); j – функция переходов (из состояния в другие состояния); y – функция выходов.

Если указанные множества бесконечные, то это уже не конечный автомат, но может быть дискретный автомат.

Если функция переходов – вероятностная, то это недетерминированный автомат.

Если в автомате выделено одно состояние, называемое начальным (обычно это y₁), то полученный автомат называется инициальным и обозначается <S,y>. Таким образом, по неинициальному автомату с i состояниями можно i различными способами определить инициальный автомат.

Функция переходов представляет собой отображение вида j: или в другом виде:

y(t+1)=j[x(t),y(t)],

где x(t),y(t),y(t+1) – конкретные символы алфавитов Х и Y соответственно в моменты автоматного времени t, t+1 (в тактах t и t+1); y(t) называется текущим внутренним состоянием при соответствующем х(t), а y(t+1) – последующим внутренним состоянием.

Иначе говоря, функция переходов определяет последующее состояние автомата по заданному текущему и входному символу.

Функция выходов представляет собой отображение вида y: Х´Y®Z или в другом виде:

z(t)=y[x(t),y(t)],

где x(t),y(t),z(t) – конкретные символы алфавитов X,Y,Z соответственно. Мы не будем особо выделять последующие значения x(t+1) и z(t+1), поэтому зависимость от t будем указывать только для внутреннего состояния, чтобы отделять y(t) от y(t+1).

Указанная функция выходов – функция так называемого автомата Мили.

В теории конечных автоматов рассматривается также автомат Мура, у которого функция выходов проще: y: или z(t)=y[y(t)].

Автомат называется комбинационным, если для любого входного символа х и любых состояний y_i, y_j j(х,y_i)=j(х,y_j)=z, иначе говоря, если выходной символ z не зависит от состояния и определяется текущим входным символом. Говорят, что у такого частного класса автомата все состояния эквивалентны и, следовательно, комбинационный автомат имеет одно состояние. Такой автомат задается тройкой:

S=<X,Z,y>.

Рассмотрим представление конечного автомата в виде «черного» ящика (рис. 51).

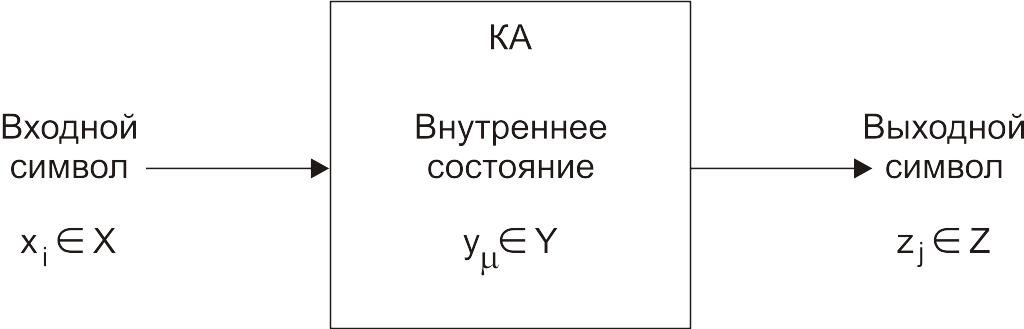
Рис. 51. Конечный автомат (КА) в виде «черного» ящика

В комбинационном автомате внутренних состояний не указывают.

Входное слово – последовательность входных символов.

Выходное слово – последовательность выходных символов, соответствующих входному слову. В конечном автомате также выделяется последовательность символов внутренних состояний, соответствующих входному слову.

Большой вклад в теорию дискретных (цифровых) автоматов внесли отечественные ученые: М.А. Гаврилов, который опубликовал первую в мире монографию «Теория релейно-контактных схем» (1950 г.), В.М. Глушков, В.Н. Рогинский, П.П. Пархоменко, В.Г. Лазарев, С.И. Баранов, А.Д. Закревский, Э.А. Якубайтис, С.В. Яблонский, В.И. Варшавский и др.

27 Описание конечных детерминированных автоматов

таблицами переходов-выходов и графами

Поскольку функции j и y определены на конечных множествах, их можно задавать таблицами. Обычно две таблицы сводят в одну таблицу j´y: и называют таблицей переходов-выходов или просто таблицей переходов (автоматной таблицей). При задании автомата ориентированным графом (орграфом), его вершины сопоставляют с внутренними состояниями, и дуги – с условиями перехода из состояния в состояние. Дуги помечают входными символами автомата. Дуги также помечают и соответствующими выходными символами, если это автомат Мили.

Рассмотрим граф переходов некоторого автомата Мили (рис. 52), Х={x₁,x₂}, Y={y₁,y₂,y₃}, Z={z₁,z₂,z₃}.

На графе автомата Мили (рис. 52) дуги помечаются дробью, где в числителе – входной символ, в знаменателе – выходной символ.

Представим этот же автомат Мили таблицей переходов (табл. 50).

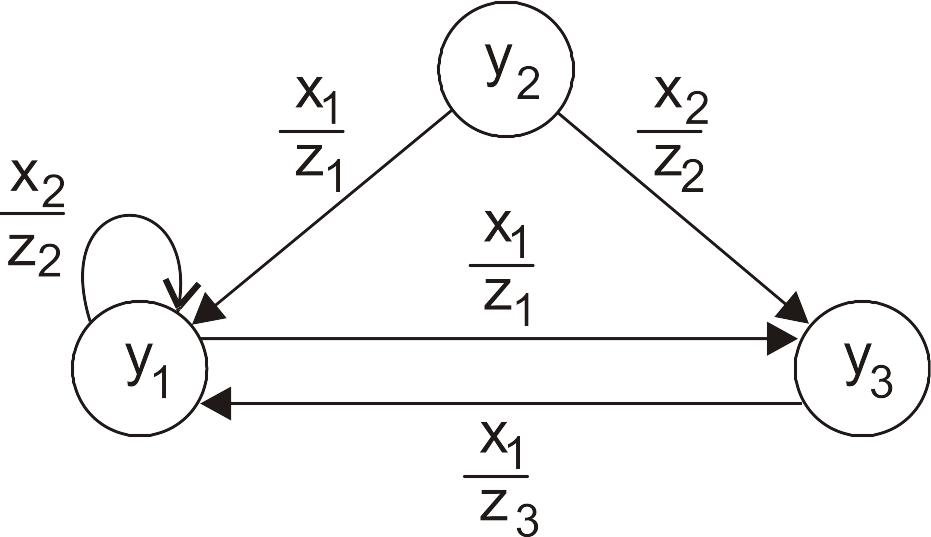
Рис. 52. Граф некоторого автомата Мили

Таблица 50

Таблица переходов выходов автомата Мили, заданного графом рис. 52

Внутреннее состояние	Входной символ
y(t)	х1	х2
y1
y2
y3		-

В клетках табл. 50 записывается дробь, в числителе которой указывается последующее внутреннее состояние y(t+1), а в знаменателе – выходной символ z(t). Это указано в специальной выноске таблицы ( ). Видно, что автомат не полностью определенный (клетка y₃х₂ не заполнена).

Рассмотрим граф некоторого автомата Мура (рис. 53), Х={x₁,x₂}, Y={y₁,y₂,y₃}, Z={z₁,z₂,z₃}:

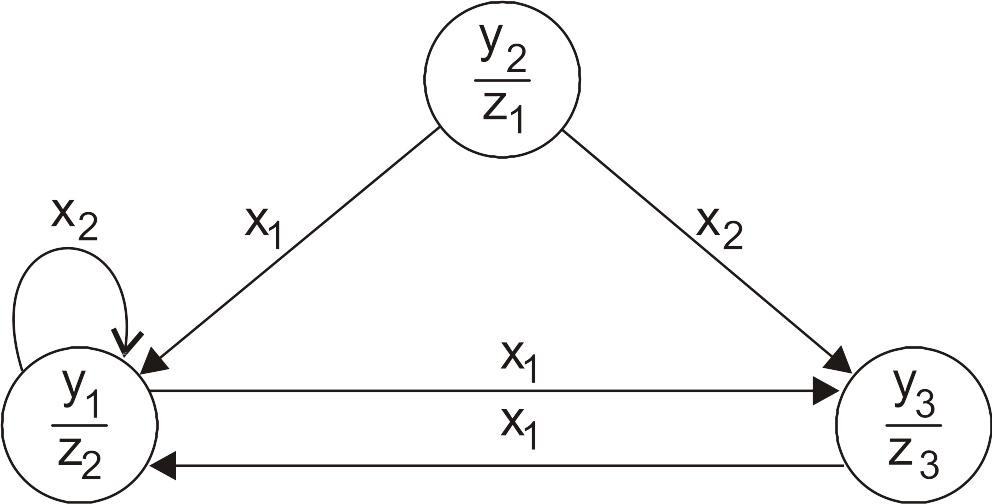
Рис. 53. Граф некоторого автомата Мура

Выходные символы в автомате Мура сопоставляются с конкретными внутренними состояниями и записываются в знаменателе дроби, помечающей внутренние состояния. Само внутреннее состояние указывается в числителе. Дуги графа автомата Мура помечаются только входными символами. Соответствующая этому автомату Мура таблица переходов представлена табл. 51.

Таблица 51

Таблица переходов-выходов автомата Мура, заданного графом рис. 53

Внутреннее состояние	Входной символ		Выходной символ
y(t)	х1	х2
y1	y3	y1	z2
y2	y1	y3	z1
y3	y1	-	z3
		y(t+1)

В клетках табл. 51, соответствующих входным символам, записывается только последующее внутреннее состояние y(t+1), что указано в специальной сноске (y(t+1)).

Комбинационный автомат задается таблицей истинности (соответствия), уже известной нам, так как граф переходов такого автомата имеет одну вершину и m петель, где m – число входных символов. Пример таблицы истинности, задающей некоторый комбинационный автомат, приведен табл. 52.

Таблица 52

Таблица истинности комбинационного автомата:

Х={x₁,x₂,х₃,х₄}, Z={z₁,z₂,z₃,z₄}

Входной символ х	Выходной символ z
x1	z2
x2	z4
x3	z1
x4	z3

В отличие от комбинационного конечного автомата, имеющего одно внутреннее состояние, конечные автоматы, имеющие больше, чем одно внутреннее состояние, называются последовательностными конечными автоматами или просто последовательностными автоматами.

Рассмотрим последовательностный автомат, заданный табл. 53. Зафиксируем начальное состояние y₁ и каждому входному слову (последовательности входных символов) a=x_j1x_j2...x_jr поставим в соответствие слово w в выходном алфавите:

w=y(x_j1,y₁)y(x_j1,x_j2,y₁)... y(x_j1,...,x_jr,y₁).

Это соответствие, отображающее входные слова в выходные, называется автоматным отображением.

Таблица 53

Таблица переходов-выходов некоторого автомата Мили

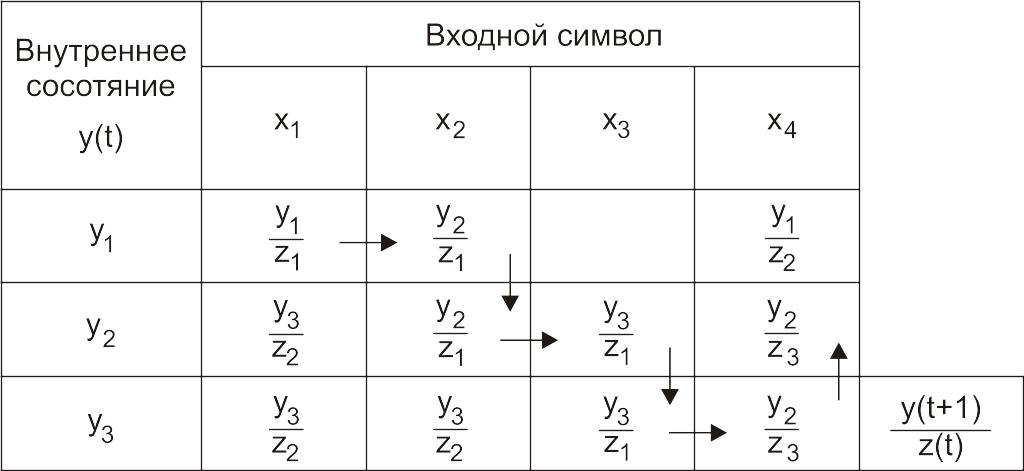
Зададим входное слово a=x₁х₂х₃х₄.

Тогда выходное слово w=z₁z₁z₁z₃.

Рассмотрим подробнее процесс формирования выходного слова:

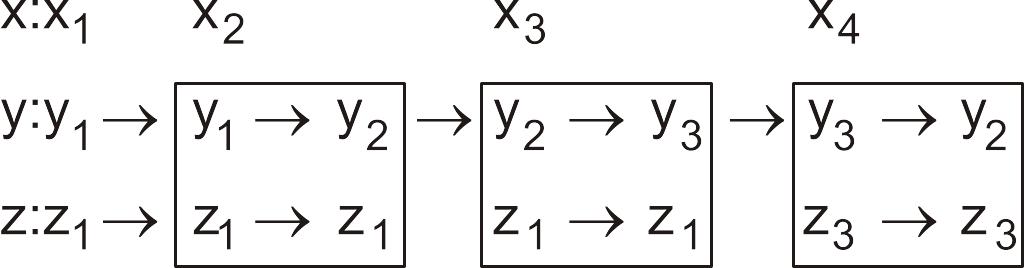
В этой последовательности указаны так называемые переходы из состояния в состояние, обведенные линией. То есть, например, при поступлении х₂ автомат сначала находится в состоянии y₁, а затем автомат переходит в состояние y₂. Указанные выше последовательности иногда изображают стрелками в таблице переходов-выходов.

Состояния y_j называют достижимыми из состояния y_i, если существует входное слово a, такое, что j(a,y_i)=y_j.

Состояния называются эквивалентными, если они соответствуют одинаковым последовательностям «входное слово – выходное слово»; причем длина такой последовательности может быть любая ³1. Например, в последовательности:

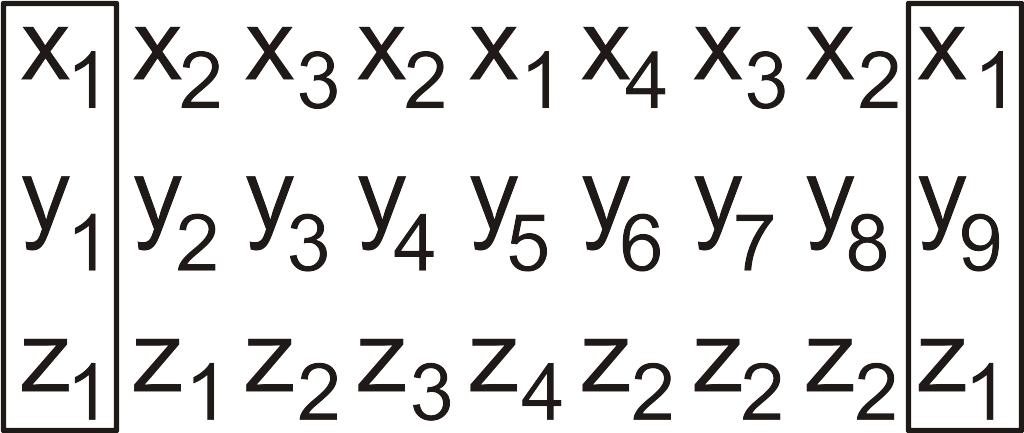
состояния y₁ и y₉ эквивалентны (длина последовательности =1), состояния y₃ и y₇ неэквивалентны, поскольку последовательность длиной 2: в первом случае , а во втором – .

Таким образом, состояние y₉ заменяется на состояние y₁.

В последовательности:

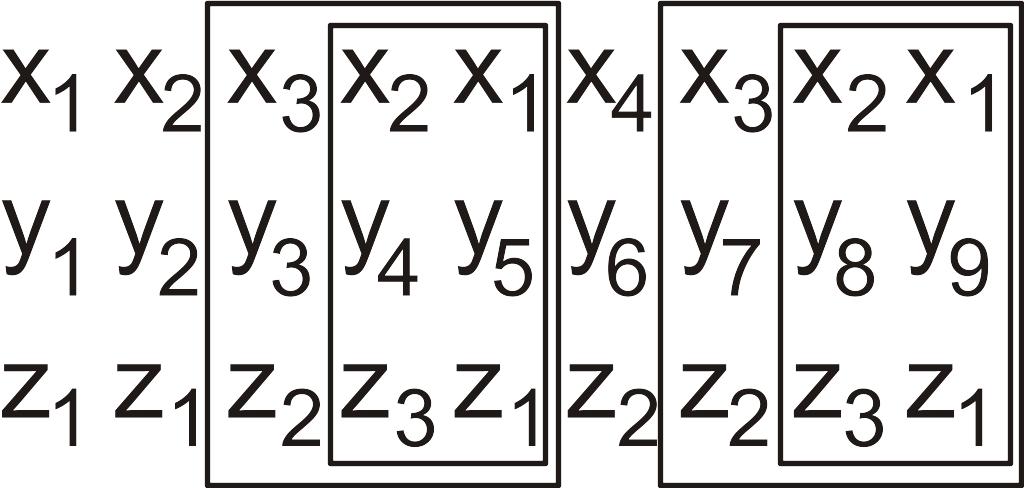
состояния y₁,у₅,y₉ также эквивалентны. Эквивалентны состояния y₃ и y₇, а также состояния y₄,y₈. Одинаковые последовательности обведены.

В этих примерах предполагается, что далее последовательности повторяются, т.е. после y₉ следует y₂,y₃ и т.д.

Таким образом, вторую последовательность можно представить в виде:

x₁ x₂ x₃ x₂ x₁ x₄ x₃ x₂ x₁

y₁ y₂ y₃ y₄ y₁ y₅ y₃ y₄ y₁

z₁ z₁ z₂ z₃ z₁ z₂ z₂ z₃ z₁

где y₉ заменено на y₁, y₇ на y₃, y₈ на y₄.

Автомат, реализующий эту последовательность, эквивалентен автомату, реализующему исходную последовательность, но имеет меньше состояний.

Автомат называется сильно связанным, если из любого его состояния достижимо любое другое состояние.

Автомат называется автономным, если его входной алфавит состоит из одной буквы X={х}. Все входные слова автономного автомата имеют вид хх...х.

28 Понятие о технической интерпретации конечных автоматов

В абстрактной теории автоматов существенна только работа автомата со словами при наличии конечной памяти.

Нас же более всего будет интересовать прикладная сторона теории конечных автоматов.

Конечный автомат представляет собой хотя и абстрактную, но с функциональной точки зрения довольно точную модель дискретного (цифрового) вычислительного или управляющего (контролирующего) устройства с конечным числом состояний [19]. Входной символ (буква) – это входной сигнал, точнее комбинация (набор) сигналов на всех входах x₁,x₂,...,x_n (это не буквы алфавита Х) устройства. Эта комбинация сигналов на дискретных входах еще называется входным вектором (набором) . Выходной сигнал (буква) – комбинация (набор) сигналов на дискретных выходах z₁,z₂,...,z_m (это не буквы алфавита Z) – выходной вектор (набор) . Входное слово – последовательность входных векторов, поступающих в дискретные моменты времени (такты) t=1,2,3...

Состоянию автомата соответствует вектор – текущее, – последующее. Этот вектор задает комбинация (набор) состояний y₁,y₂,...,y_s (это не буквы алфавита Y) элементов памяти автомата.

Выходное слово – последовательность выходных векторов в дискретные моменты времени.

Комбинационный автомат интерпретируется некоторой переключательной схемой или схемой из функциональных элементов (рис. 54).

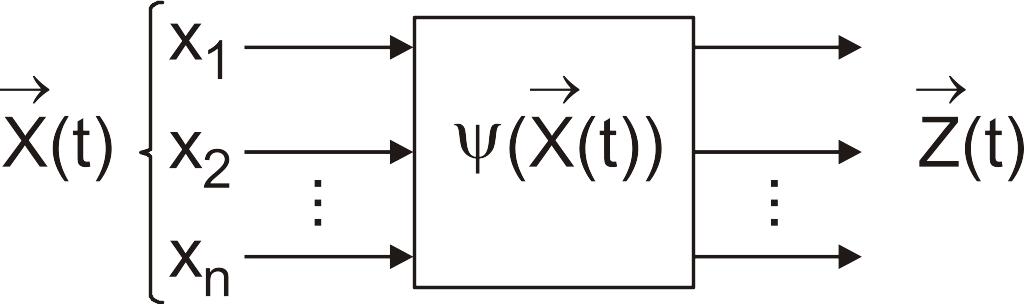
Рис. 54. Техническая интерпретация комбинационного автомата

Функция выходов y( )= (отображение ) реализуется, например, с использованием функционально-полного набора элементов, соответствующих логическим функциям, составляющим функционально-полную систему. При этом y( ) представляется в виде суперпозиции этих логических функций. Вопрос представления логических функций в разных базисах и получения соответствующих схем, так же, как и вопрос получения переключательных комбинационных схем, рассматривается особо.

Последовательностный автомат интерпретируется схемой с обратными связями в виде так называемых задержек на один такт (рис. 55).

Дело в том, что проблема автоматной полноты (для последовательностного автомата) алгоритмически неразрешима, в отличие от проблемы полноты для переключательных функций (для комбинационного автомата) [19].

Однако в теории конечных автоматов доказано, что последовательностный автомат может быть реализован как композиция комбинационного автомата и двоичных задержек на один такт в цепи обратной связи [19].

На рис. 55 ЛП – логический преобразователь – комбинационный автомат, реализующий функции переходов j и выходов y, D – задержки (от слова delay – задержка). В дальнейшем мы покажем, что в качестве задержек могут использоваться так называемые элементы памяти.

В автомате Мура функции выходов реализуются отдельно (рис. 56), т.е. имеются два логических преобразователя (ЛП1, ЛП2).

Таким образом, в автомате Мили выходной вектор в некоторый момент времени зависит как от текущего состояния автомата, так и от входного вектора в этот момент времени.

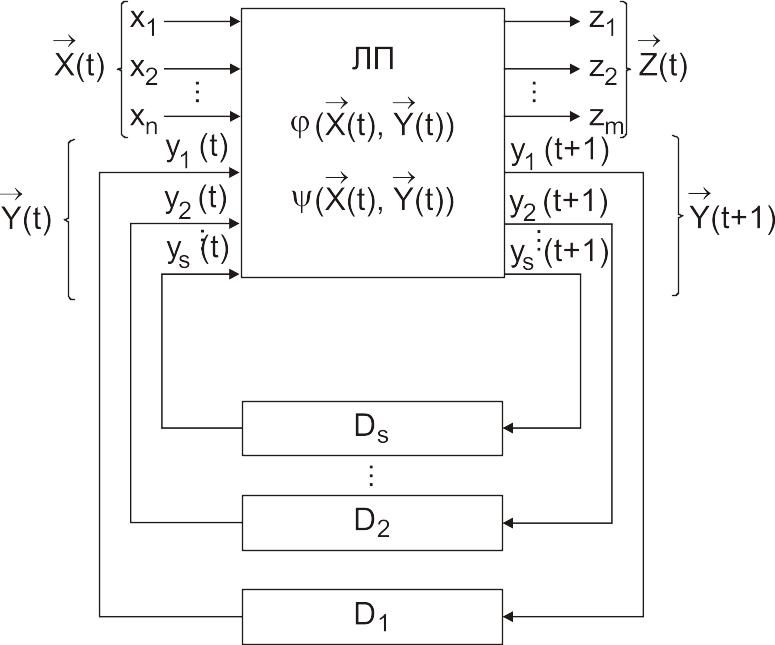
Рис. 55. Техническая интерпретация автомата Мили

В автомате Мура выходной вектор в некоторый момент времени непосредственно не зависит от входного вектора, а однозначно определяется внутренним состоянием в этот же момент времени. Поэтому автоматы Мура менее быстродействующие, чем автоматы Мили. Автоматы могут быть описаны также уравнением (функциями) переходов и выходов (аналитически).

Реальные дискретные автоматы функционируют по тактам. Такт – отрезок времени произвольной длины, в течение которого состояние автомата остается неизменным. Такты могут обозначаться моментом времени t₀,t₁,t₂,...,t_m, причем последовательность номеров тактов образует дискретное (автоматное) время.

В теории конечных автоматов принимается допущение, что переход из одного внутреннего состояния в другое происходит скачкообразно, мгновенно. В реальных автоматах всегда имеет место конечная длительность переходных процессов.

Такты бывают устойчивыми и неустойчивыми. Такт называют устойчивым, если очередное изменение состояния автомата происходит только за счет изменения состояния входов, т.е. после поступления очередного входного набора. Такт называют неустойчивым, если очередное изменение состояния автомата происходит только за счет изменения внутреннего состояния – элементов памяти. Устойчивые такты в клетках таблицы переходов-выходов обычно отмечают кружками. Дискретные автоматы, в которых изменение внутренних состояний происходит в определенные моменты времени, определяемые специальным генератором синхронизирующих импульсов, называют синхронными. При этом, как правило, все тактовые интервалы равны.

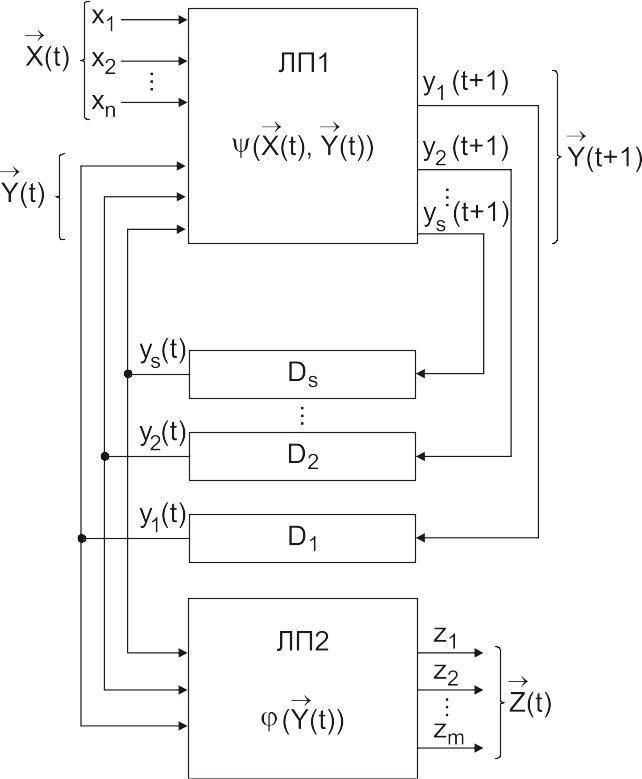
Рис. 56. Техническая интерпретация автомата Мура

Автоматы, в которых переходы из одного состояния в другое заранее не определены и могут совершаться в произвольные моменты времени через неравные промежутки времени, называют асинхронными.

Дискретный автомат – это устройство дискретного преобразования информации: при подаче на его вход некоторой последовательности входных наборов он формирует некоторую последовательность выходных наборов.

Для реального автомата актуальным является наиболее экономичная его реализация из всех возможных реализаций в смысле затрат элементов, энергопотребления и т.д.

Можно интерпретировать автомат не только как устройство. Известно, что всякое управление (вычисление, контрольную операцию) можно реализовать как аппаратурно (в виде устройства), как и программно (в виде программы ЭВМ). Это приводит к более общему толкованию конечных автоматов как алгоритмов с конечной памятью, многие свойства которых можно исследовать и безотносительно к способу их реализации [19].

Имеется еще и другая интерпретация автоматов. Фон Нейман рассматривал автоматы как удобный язык для описания основных законов взаимодействия сложных систем, т.е. по существу, как метаязык кибернетики [19].

Задачами теории конечных автоматов являются:

1) изучение возможностей автоматов в терминах множеств слов, с которыми они работают (распознавание входных последовательностей – слов), формирование требуемых выходных, т.е. автоматных отображений;

2) распознавание различных свойств автоматов;

3) описание автоматов (анализ) и их реализация, т.е. представление автомата как структуры, состоящей из объектов фиксированной сложности (синтез) [19].

При синтезе автоматов выделяют следующие этапы:

1) абстрактный синтез, или формализация условий работы, когда от некоторого высокоуровневого описания автомата (например, на естественном языке – в виде словесной формулировки) переходят к математической модели. Такой моделью может быть таблица истинности для комбинационного автомата, таблица переходов-выходов для последовательностного автомата. В свою очередь по этим моделям получают переключательные функции в символической форме;

2) структурный синтез – производится минимизация переключательных функций, описывающих автомат, выполняется их представление в виде, соответствующем заданному базису реализации.

Эти два этапа называют логическим проектированием. Их результатом является функциональная схема автомата (например, функциональная электрическая схема);

3) физический синтез – решаются вопросы построения принципиальной схемы (например, принципиальной электрической схемы), создания топологии кристалла микросхемы, обеспечения надежности, помехоустойчивости и в дальнейшем изготовления автомата.

При синтезе последовательностного автомата проводится и минимизация числа состояний автомата – путем сжатия таблицы переходов-выходов.

29 Синтез комбинационных автоматов в заданном базисе

Синтез комбинационных автоматов.

При синтезе комбинационных автоматов (после этапа абстрактного и структурного синтеза имеются соответствующие переключательные функции) требуется получить схему автомата, например, в виде переключательной схемы или схемы из функциональных (логических) элементов.

Синтез переключательной схемы.

Пусть задана переключательная функция Получим переключательную схему (рис. 57).

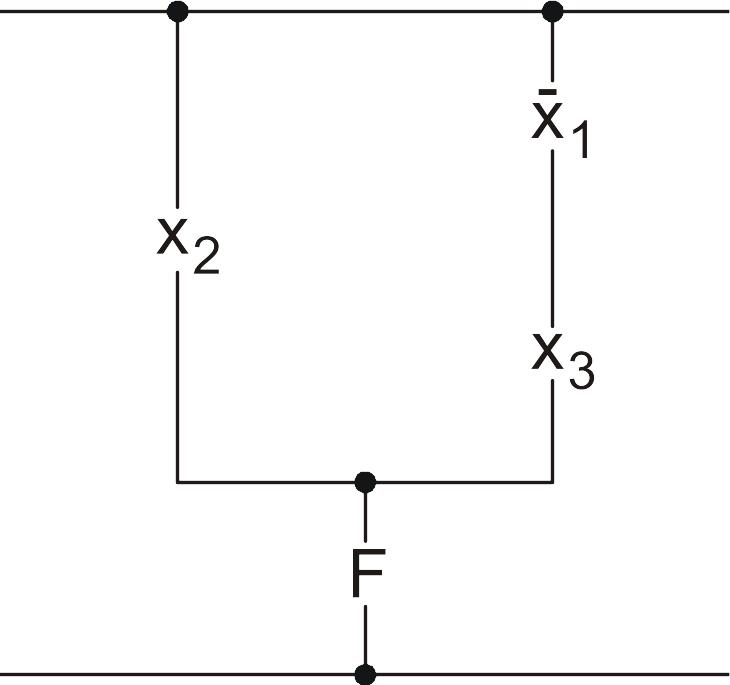
Рис. 57. Переключательная схема,

реализующая функцию

На рис. 57 верхняя и нижняя горизонтальные линии обозначают, например, полюсы источника питания, а буква F – некоторый элемент, срабатывающий в случае равенства функции логический единице, т.е. в случае наличия цепи к верхнему полюсу. Символами переменных х₁,х₂,х₃ могут обозначаться, например, контакты некоторых датчиков, а F – обмотка реле, контакт которого включает некоторый исполнительный орган (вентилятор, сирену, нагреватель и др. элементы автоматики). Соответствующая релейно-контактная схема изображена на рис. 58.

Часто датчики подключаются не непосредственно в цепи реализации переключательных функций, а через реле-повторители (рис. 59).

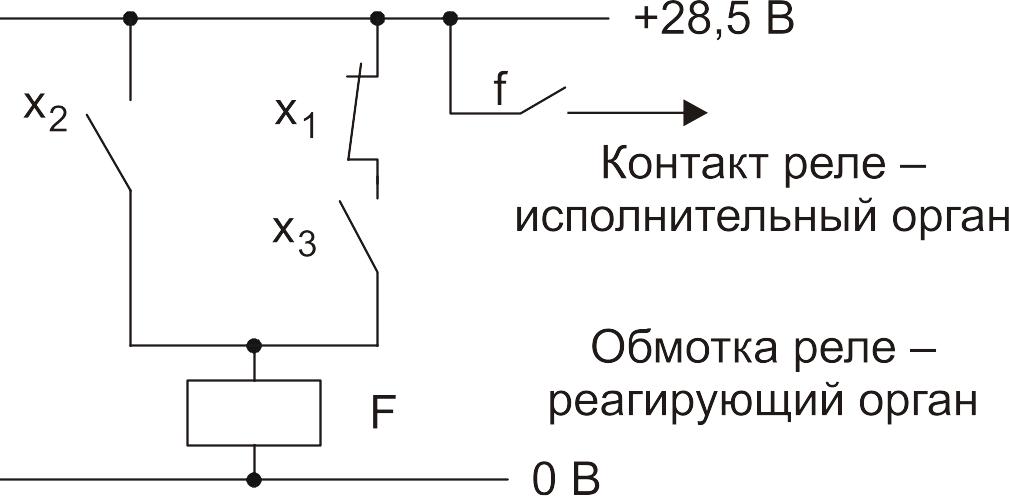
Рис. 58. Релейно-контактная схема

реализации логической функции

Рис. 59. Релейно-контактная схема реализации переключательной функции с реле-повторителями сигналов датчиков

Синтез комбинационных автоматов на основе функциональных (логических) элементов по сравнению с переключательными схемами требует особого представления логической функции – в виде суперпозиции операций заданного базиса.

Синтез в базисе И, ИЛИ, НЕ.

Наиболее просто это сделать, если задать базис И, ИЛИ, НЕ. Предполагается, что переключательная функция представлена в ДНФ.

Пусть, например, задана следующая переключательная функция: z(аbсdx₂x₁)=

Получим схему в базисе И, ИЛИ, НЕ (рис. 60).

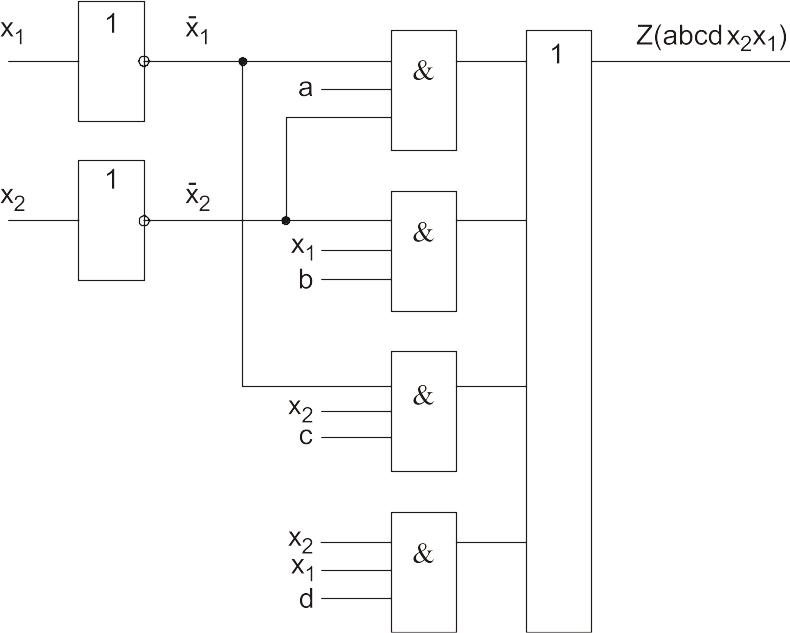
Рис. 60. Схема в базисе И, ИЛИ, НЕ без ограничения числа входов

функциональных элементов

Схема рис. 60 изображена в предположении, что число входов элементов не ограничено.

Если же должны использоваться только двухвходовые элементы, т.е. все операции бинарные (кроме инверсии), то схема будет выглядеть так, как изображено на рис. 61.

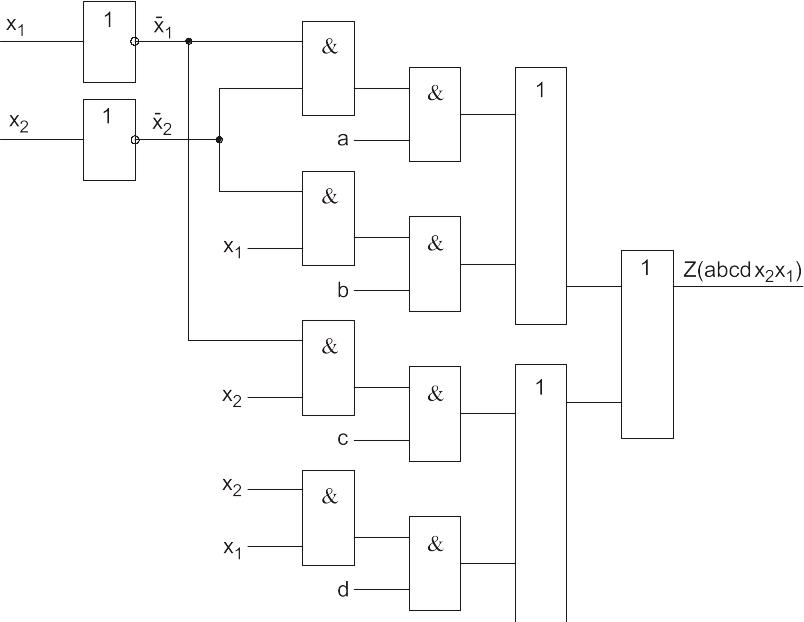
Рис. 61. Схема с учетом наличия только двухвходовых элементов И, ИЛИ

Синтез методом каскадов.

При синтезе комбинационных автоматов используется метод каскадов, основанный на разложении Шеннона:

f(x₁,...,x_i,...,x_n)=x_if(x₁,...,1,...,x_n)Ú _if(x₁,...,0,...,x_n)=x_if(1)Ú _if(0).

Такое разложение позволяет исключать переменные и понижать размерность по каскадам до тех пор, пока остаточные функции не будут иметь простой вид и их реализация не будет представлять трудности [9].

Реализуем вышерассмотренную функцию z(аbсdx₂x₁) методом каскадов с использованием блоков исключения переменной вида x_if(1)Ú _if(0), которые легко реализуются в базисе И, ИЛИ, НЕ.

Очевидно, что:

z(аbсdx₂x₁)= ,

т.е. , , которые реализуются на двухвходовых элементах И, ИЛИ. Проводить дальнейшее разложение нет необходимости. Соответствующая схема комбинационного автомата изображена на рис. 62.

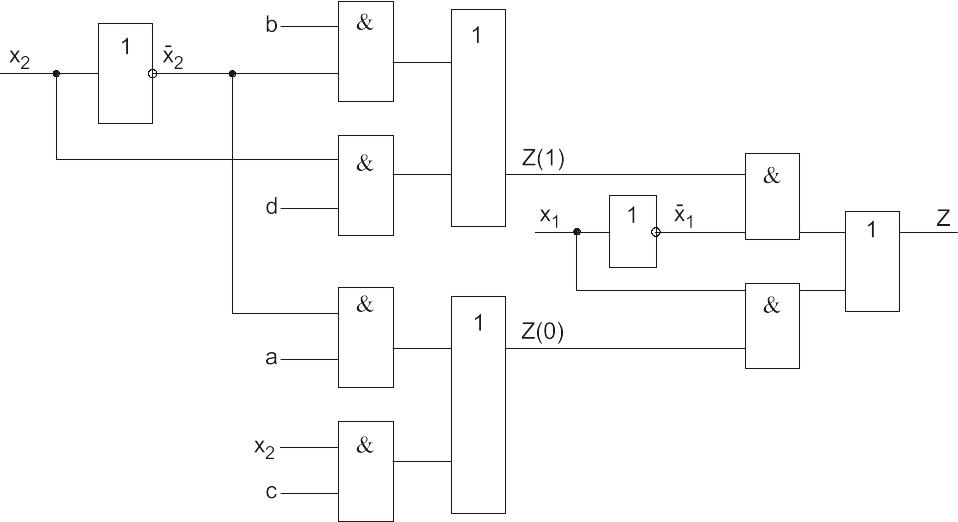
Рис. 62. Схема, построенная по методу каскадов

Интересно, что схема на рис. 62, построенная по методу каскадов, проще в смысле числа элементов – для ее построения необходимо 11 элементов (9 двухвходовых и 2 инвертора). Сравните ее со схемой на рис. 61, для построения которой потребовалось 13 элементов (11 двухвходовых и 2 инвертора).

В общем случае сложность остаточных функций зависит от порядка исключения переменных и оптимальное их исключение ищут специальными методами, основанными на понятии булевой производной:

=f(x₁,x₂,...,x_i-1,1,x_i+1,...,x_n)Åf(x₁,x₂,...,x_i-1,0,x_i+1,...,x_n),

где Å – сумма по модулю 2 [9].

При использовании базисов, отличных от рассмотренного базиса И, ИЛИ, НЕ, блоки исключения переменных и блоки реализации остаточных функций реализуются в заданном базисе.

Например, в импликативном базисе {®,0}:

=(а®(b®0))®0.

Синтез в базисах И-НЕ, ИЛИ-НЕ.

Наиболее часто используются базисы, состоящие из одной функции: И-НЕ, ИЛИ-НЕ.

Представление переключательной функции в этих базисах требует использования только этих операций с учетом ограничений по числу входов соответствующих элементов. Для этого используется закон Де Моргана:

f(аbсd)= = = – это представление в базисе И-НЕ.

– это представление в базисе ИЛИ-НЕ.

Соответствующие схемы представлены на рис. 63.

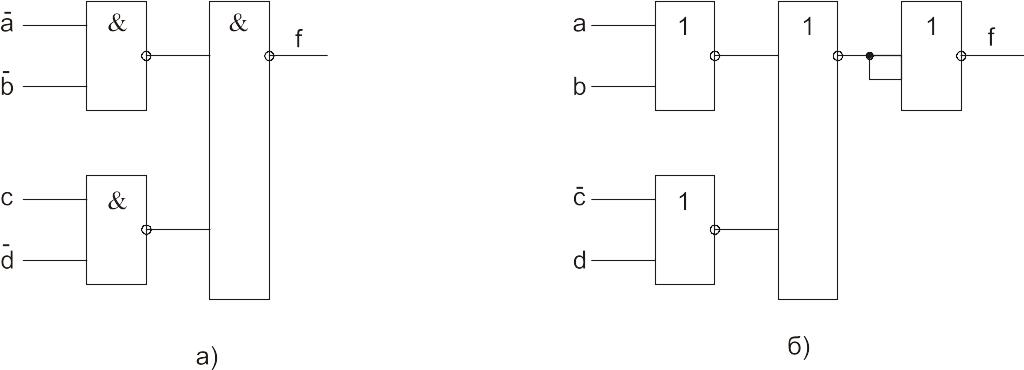
Рис. 63. Реализация логической функции f(аbсd)=

в базисе 2И-НЕ (а) и 2ИЛИ-НЕ (б),

т.е. для двухвходовых элементов И-НЕ, ИЛИ-НЕ

В случае превышения ограничения по числу входов элементов следует еще раз применить закон Де Моргана, например:

т.е. получили только одноместные и двухместные операции И-НЕ.

Синтез в базисе Жегалкина.

Полиномом Жегалкина называется представление логической функции в базисе {Å,И,НЕ} (имеется соответствующая алгебра Жегалкина). В данном представлении инверсия реализуется как сумма по модулю 2 с константой 1.

Для представления ДНФ в виде полинома Жегалкина необходимо выразить дизъюнкцию через конъюнкцию и инверсию.

Например:

хÚy= =(хÅ1)(yÅ1)Å1=

=xyÅxÅyÅ1Å1=xyÅxÅy.

(1Å1=0).

Пример. Представить в виде полинома Жегалкина логическую функцию xÚyÚz.

xÚyÚz= =(хÅ1)(yÅ1)(zÅ1)Å1=(xyÅxÅyÅ1)(zÅ1)Å1=

=xyzÅxzÅyzÅxyÅxÅyÅ1Å1=xyzÅxzÅyzÅxyÅxÅy.

Для преобразования полинома Жегалкина используются обычные приемы элементарной алгебры (исключение составляет равносильность аÅа=0).

Полином Жегалкина может быть получен по таблице истинности путем суммирования по модулю 2 конъюнкций переменных без инверсии x_i или инверсных переменных (x_jÅ1) соответствующих рабочих наборов.

Например, получим полином Жегалкина для функции f, таблица истинности которой имеет вид табл. 54.

Таблица 54

Таблица истинности

x	y	z	f
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Тогда получим:

f=(xÅ1)(yÅ1)zÅ(xÅ1)y(zÅ1)Åx(yÅ1)(zÅ1)Åxyz=

=(xyÅxÅyÅ1)zÅ(xzÅxÅzÅ1)yÅx(yzÅyÅzÅ1)Åxyz=

=xÅyÅz,

что и требовалось доказать, ибо и рассматривалась функция сложения по модулю 2 трех аргументов.