
Примеры решения задач
Задача 1. Два неподвижных электрических заряда q1=9мкКл и q2=-4мкКл расположены в воздухе на расстоянии 10см друг от друга. 1). На каком расстоянии от первого нужно поместить третий заряд q3, чтобы он находился в равновесии? 2). При какой величине заряда q3 система трёх зарядов будет находиться в равновесии?
1 этап: общий анализ ситуации. Заряд q3 будет находиться в равновесии, если силы, действующие на него со стороны первых двух, равны по модулю и противоположны по направлению (см. рис. 1) :
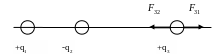
Рис.1. Равновесие заряда q3.
Из рисунка видно, что заряд q3 будет находиться в равновесии при выполнении следующих условий:
1. Заря q3 находится ближе к меньшему q2 и дальше от большего q1.
2. Все три заряда находятся на одной
прямой, так как только в этом случае
силы
![]() и
и
![]() могут уравновесить друг друга.
могут уравновесить друг друга.
3. Силы и имеют противоположные направления, что возможно, если разноимённые заряды q1 и q2 располагаются по одну сторону от заряда q3.
4. Если заряды q1 и q2 одноимённые, то заряд q3 должен располагаться ними (см. рис. 2).
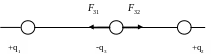
Рис. 2. Равновесие заряда q3 при взаимодействии с одноимёнными зарядами q1 и q2.
2 Этап: общее решение задачи.
 Модуль силы взаимодействия электрических
зарядов определяется законом Кулона:
Модуль силы взаимодействия электрических
зарядов определяется законом Кулона:
![]() (1)
(1)
Здесь q1 и q2 модули зарядов взаимодействующих частиц, r– расстояние между ними, ε – диэлектрическая проницаемость среды (для воздуха ε=1).
Для решения задачи обозначим через а расстояние между зарядами 1 и 2, а через х искомое расстояние между первым и третьим зарядами – рис. 3.
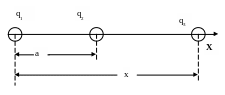
Рис. 3. Схема расположения зарядов.
1). Условие равновесия третьего заряда
![]() или в скалярном виде
или в скалярном виде
![]() .
Используя закон Кулона (1), последнее
равенство запишем в виде:
.
Используя закон Кулона (1), последнее
равенство запишем в виде:
![]() (2).
(2).
В результате несложных преобразований
равенство (2) приводится к виду:
![]() (3).
(3).
Решая это квадратное уравнение, получим:
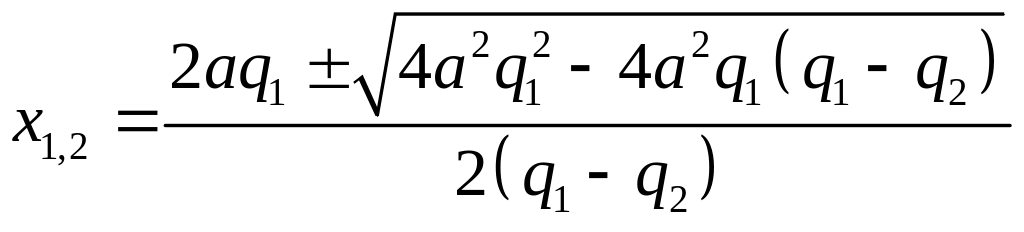
или, после упрощения:
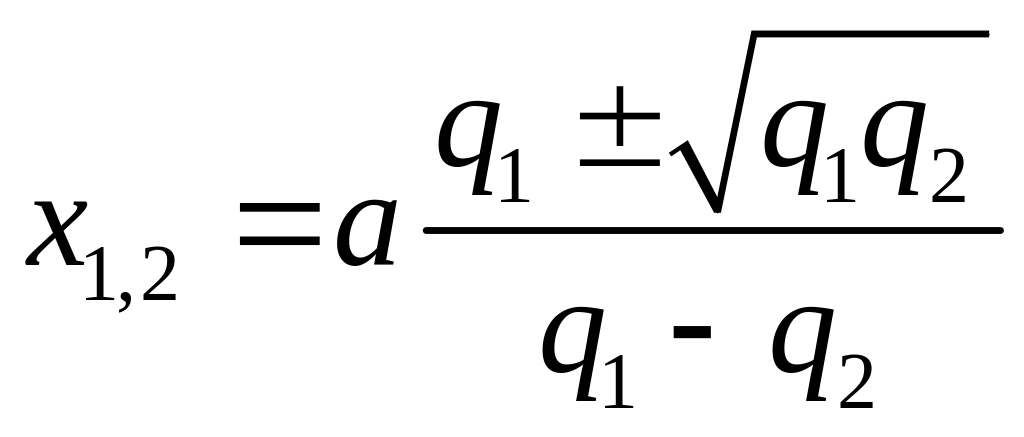 .
(4)
.
(4)
Подставляя исходные данные, найдём корни этого уравнения:
![]() ,
(5а)
,
(5а)
![]() ,
(5б)
,
(5б)
Учитывая, что по условиям задачи заряды
q1 и q2
разноимённые и искомое расстояние х
больше расстояния между зарядами а
(см. рис. 3), находим окончательный ответ:
![]() .
.
В уравнении (4) нет величины заряда q3, следовательно, при неподвижных первых двух зарядах равновесие третьего заряда не зависит от его величины и знака.
2). Система трёх зарядов будет находиться в равновесии при выполнении двух условий:
- если модули всех сил взаимодействия между зарядами будут равны;
- силы, действующие на каждый заряд, направлены в противоположные стороны (см. рис. 4).
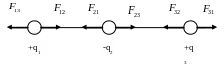
Рис. 4. Равновесие системы трёх зарядов.
Первое условие выполняется, если
,
![]() и
и
![]() .
Так как,
.
Так как,
![]() ,
то система трёх зарядов будет в равновесии,
если
,
то система трёх зарядов будет в равновесии,
если
![]() :
:
![]() .
.
Отсюда находим модуль заряда q3:
![]() или
или
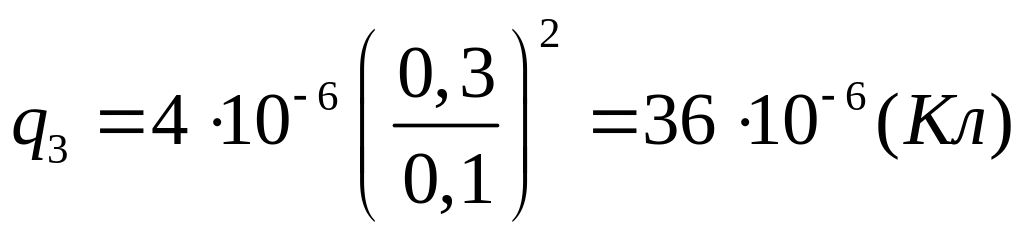 .
.
В соответствии со вторым условием заключаем, что заряд q3 должен быть положительным.
Проверка размерности:
Из уравнения (4) получим
![]()
Ответ:
![]() ;
;
![]() .
.
Примечание: можно показать, что равенство (5б) является решением при условии, что заряды q1 и q2 одноимённые (рис. 5).
a
x
Рис. 5. Пример равновесия системы трёх зарядов.
Задача 2. Точечные заряды
![]() ,
,
![]() и
и
![]() ,
расположены в воде на расстояниях
10 см друг от друга. Определить силу,
действующую на третий заряд со стороны
первых двух.
,
расположены в воде на расстояниях
10 см друг от друга. Определить силу,
действующую на третий заряд со стороны
первых двух.
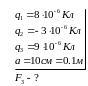 Решение.
Решение.
Из условий задачи следует, что электрические заряды располагаются в вершинах правильного треугольника с длиной сторон 0.1м (см. рис. 1). Диэлектрическая проницаемость воды ε=81.
М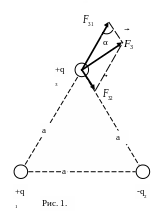 одуль
силы взаимодействия электрических
зарядов определяется законом Кулона:
одуль
силы взаимодействия электрических
зарядов определяется законом Кулона:
(1).
Из уравнения (1) следует, что модули сил, действующих на третий заряд со стороны первого и второго, равны соответственно:
![]() и
и
![]() (2)
(2)
Из рис.1 видно, что модуль результирующей
силы, действующей на третий заряд
![]() можно найти по теореме косинусов:
можно найти по теореме косинусов:
![]()
С учетом равенств (3) получим
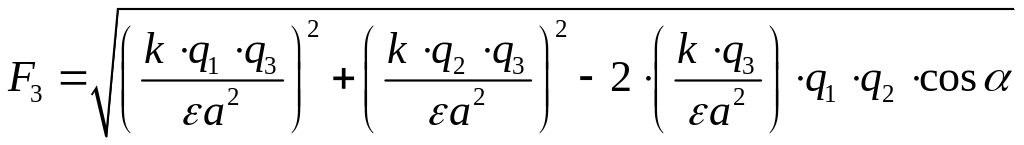 .
.
После упрощения это уравнение примет
вид
![]() .
(3)
.
(3)
Подставляя исходные данные и учитывая,
что угол
![]() найдём окончательный ответ:
найдём окончательный ответ:
![]() .
.
Проверка размерности:
Из уравнения (3) получим
![]()
Ответ: F3=0,7 Н
Задача 3. Два одинаково заряженных маленьких шарика массой по 1 г каждый подвешены в одной точке на шелковых нитях длиной по 1 м. Определите величину заряда каждого шарика, если нити отклонилась на угол 300 от вертикали.
