Задания и порядок их выполнения

1. Пусть A ={a, b, c}, B ={d, e}, C ={a, b, c, d, e}. Тогда множество A равно:

а)

б)

в)

г)

Ответ: в).

2. Даны множества: А = {1, 4, 5, 7} и B = {4, 5, 9, 10, 12}. Найти: а) А  В; б) А В; в) В \ А; г) A  B.

Решение

А  В = {1, 4, 5, 7, 9, 10, 12}. А  В = {4, 5}. В \ А = {1, 7}. A  B = {1, 7, 9, 10, 12}.

3. Даны два множества: А = {6k + 5 k = 0, 1, 2, …} и B = {3m + 2  m = 0, 1, 2, …}. Найти: а) А  В; б) А  В; в) В \ А; г) A  B.

Решение

1. Определить, какие элементы принадлежат множествам:

А = {5, 11, 17, 23, 29, …}. B = {2, 5, 8, 11, 14, 17, …}.

2. Найти объединение, пересечение, разность и симметрическую разность множеств:

А  В = В. А  В = А. В \ А = {2, 8, 14, 20, … } = {6k + 2  k = 0, 1, 2, …}.

A  B = {2, 8, 14, …} = {6k + 2  k = 0, 1, 2, …}.

4. Заданы множества A = {2, a} и B ={1, с}. Найти декартово произведение множеств .

Ответ: {(2, 1), (2, c), (a, 1), (а, с)}.

5. Установите соответствие между множествами и верными для них высказываниями:

1) А – множество студентов вашего вуза старше 17 лет

2) В – множество натуральных чисел, меньших 1

3) С – множество натуральных чисел, больших 1

А) множество является пустым

Б) множество бесконечно

В) ничего определённого о множестве сказать нельзя

Г) множество конечно

Ответ: 1 – Г; 2 – А; 3 – Б.

6. Заданы множества C = {1, 2, 3} и D = {0}. Верными для них являются утверждения:

а) Множество С не является подмножеством множества D

б) Множество С конечно

в) Множество D конечно

г) Множество D не является подмножеством множества С

д) Множества С и D равны

Ответы: а), б), в) и г).

7. Заданы произвольные множества А, В и С. Расположите указанные ниже множества так, чтобы каждое из них было подмножеством следующего за ним:

А)

Б)

В)

Г)

Решение. Множества, полученные в результате выполнения указанных операций, отметим штриховкой:

В) А) Б) Г)

Ответы: 1 – В); 2 – А); 3 – Б); 4 – Г).

7^. Заданы произвольные множества А, В и С. Расположите указанные ниже множества так, чтобы каждое из них было подмножеством следующего за ним ...

А)

Б)

В)

Г)

Решение. Множества, полученные в результате выполнения указанных операций, отметим штриховкой:

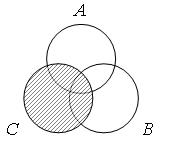
Б) А) Г) В)

Ответы: 1 – Б); 2 – А); 3 – Г); 4 – В).

8. Из 20 студентов двое могут играть только в шахматы, трое – только в шашки, шестеро – только в футбол. Никто не умеет играть во все три игры. Один играет в шахматы и шашки, трое  в футбол и шахматы. Сколько студентов играют одновременно и в футбол и в шашки?

Решение. Обозначим через А множество студентов, играющих в шахматы, через В  в шашки, через С  в футбол. По условию задачи: А  В  С = 20, А  В = 1,  А  С  =3, А  В  С =  (никто не умеет играть сразу в три игры). Требуется определить количество элементов в пересечении В  С.

Изобразим эти множества на диаграмме Эйлера-Венна:

Из диаграммы видно, что множество В  С = 20 – 1 – 2 – 3 – 6 – 3 = 5. Значит, играть в футбол и шашки умеют 5 студентов.

Ответ: 5 студентов.

9. Если отношение задано неравенством: , то данному отношению принадлежит следующая пара чисел ...

а) (0;0)

б) (5;2)

в) (2;-1)

г) (2;2)

Ответ: г).

9*. Какая пара чисел принадлежит отношению:

Отношение	а)	б)	в)	г)	Ответ
	(1;1)	(5;1)	(0;0)	(5;2)	б)
	(0;2)	(2;2)	(1;5)	(5;1)	г)
	(1;1)	(0;1)	(-1;0)	(-1;-1)	а)
	(1;-10)	(-5;1)	(1;-4)	(-4;1)	в)
	(-5;1)	(-4; 3)	(3;-4)	(1;-2)	в)