Математическая формулировка задачи.
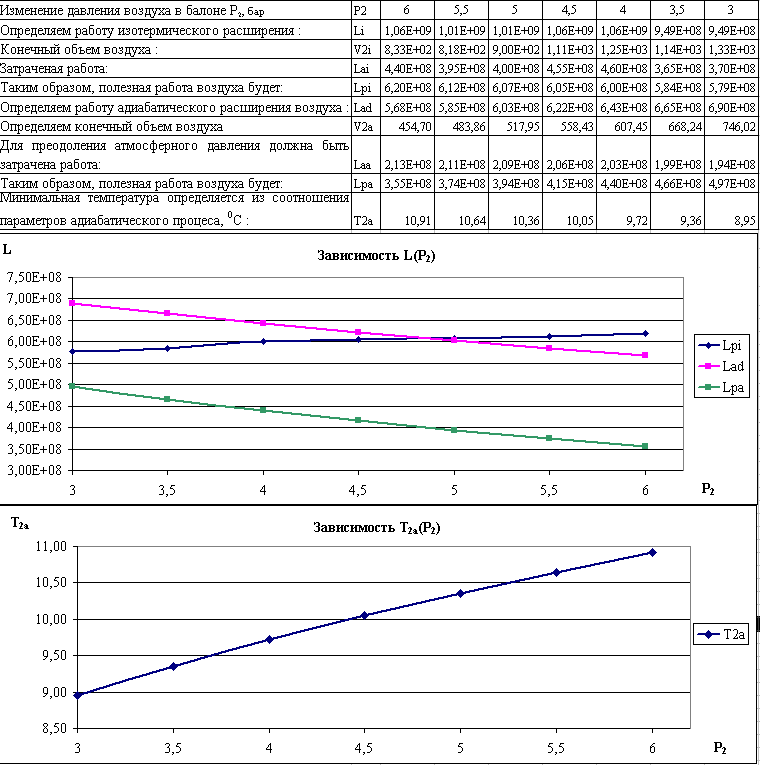
Определяем работу изотермического расширения :
,
Конечный объем воздуха :
,
Для преодоления атмосферного давления должна быть затрачена работа:
.
Таким образом, полезная работа воздуха будет:
Определяем работу адиабатического расширения воздуха :
,
Определяем конечный объем воздуха :
.
Для преодоления атмосферного давления должна быть затрачена работа:
Таким образом, полезная работа воздуха будет:
.
Минимальная температура определяется из соотношения параметров адиабатического процеса :
, 
.
Построить
графики зависимости:
(Р2),
(Р2),
(Р2),
Т2(Р2)
Расчетные данные к заданию 2.:
Начальные данные |
Варианты |
||||||||||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
Давление воздуха в балоне Р1, бар |
50 |
45 |
45 |
50 |
50 |
40 |
40 |
42 |
42 |
44 |
44 |
46 |
46 |
52 |
52 |
52 |
54 |
54 |
56 |
56 |
58 |
58 |
60 |
60 |
62 |
Начальная температура воздуха в балонеТ1, 0С |
20 |
15 |
25 |
22 |
24 |
16 |
17 |
21 |
31 |
28 |
26 |
14 |
18 |
19 |
25 |
23 |
27 |
19 |
15 |
18 |
20 |
22 |
23 |
15 |
15 |
Изменение давления воздуха в балоне Р2, бар |
6-3 |
3-1 |
3-1 |
6-4 |
4-2 |
6-2 |
5-2 |
6-3 |
3-1 |
2,5-1 |
4-1 |
4-2 |
6-2 |
5-2 |
6-3 |
3-1 |
4-1 |
6-2 |
5-2 |
6-3 |
3-1 |
4-1 |
6-2 |
5-2 |
6-3 |
Шаг изменения Р2, бар |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
Перевод единиц измерения в систему СИ: давления бары в Па – 1 бар=105 Па, температуру 0С в К – 1С=273К
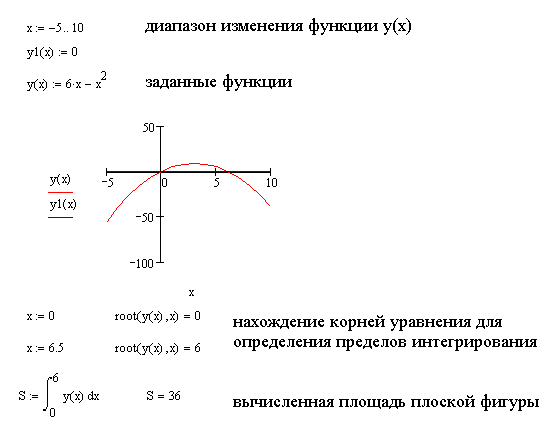
Пример выполнения задания.
РЕШЕНИЕ ЗАДАЧ В СРЕДЕ MATHCAD
Задание 1.
Вычислить площадь плоской фигуры ограниченной линиями.
Рекомендации к выполнению задания
Как известно, определённый интеграл от неотрицательной непрерывной функции есть площадь соответствующей криволинейной трапеции. В этом заключается геометрический смысл определённого интеграла, на этом основано его применение к вычислению площадей плоских фигур.
Рассмотрим несколько случаев для определения определённого интеграла.
Случай 1.
Криволинейная
трапеция АВСD
ограниченна графиком неотрицательной
непрерывной функции у=f(х),
х
[a,b],
отрезком [a,b]
оси Ох, отрезками прямых х=а и х=b
(a<b),
в этом случае площадь криволинейной
трапеции вычисляется по формуле
(1)
Случай 2.
Если данная функция отрицательная непрерывная функция у=-f(х), х [a,b], тогда получим, что площадь криволинейной трапеции А’В’С’D’ ограниченная графиком функции у=-f(х), отрезком [a,b] оси Ох, отрезками прямых х=а и х=b (a<b), в этом случае площадь криволинейной трапеции вычисляется по формуле
(2)
Случай 3.
Если данная функция у=f(х), х [a,b], непрерывна на отрезке [a,b] функция график которой пересекает отрезок [a,b] оси Ох в конечном числе точек и ограниченная графиком функции у=f(х), отрезком [a,b] оси Ох, отрезками прямых х=а и х=b (a<b) вычисляется по формуле
(3)
Случай 4.
Если площадь искомой фигуры Q, ограниченна отрезками прямых х=а и х=b (a<b) и графиками неотрицательных непрерывных функций f1(х), х [a,b] и f2(х), х [a,b], то такую фигуру можно рассматривать как разность криволинейных трапеций и с учетом (1) получаем формулу для вычисления площади фигуры
(4)
Случай 5.
Если требуется вычислить площадь более сложной фигуры, то стараются выразить искомую площадь в виде алгебраической суммы площадей некоторых криволинейных трапеций. Пусть кривые АВ, ВС и Ас соответственно графики следующих функций: у=f1(х), х [a,b], у=p(х), х [a,с], у=d(x) х [c,b] тогда получим:
(5)
Варианты заданий.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11
12
При х
13.
14.
15.
16
17
18.
19.
20.
Пример выполнения задания.
