
- •«Непараметрические критерии однородности статистических данных»
- •Список обозначений
- •Введение
- •1. Непараметрические (свободные от распределения) критерии однородности статистических данных
- •1.1. Непараметрические критерии сдвига
- •1.1.1. Сравнение параметров сдвига двух совокупностей
- •1.1.1.1 Быстрый (грубый) критерий Кенуя
- •1.1.1.2. Быстрый (грубый) ранговый критерий
- •1.1.1.3. Критерий Манна-Уитни-Вилкоксона
- •1.1.1.4. Критерий Фишера-Йэйтса-Терри-Гёфдинга
- •1.1.1.5. Критерий Ван дер Вардена
- •1.1.1.6. Медианный критерий
- •1.1.2.2. Критерий Неменьи
- •1.1.2.3. Критерий Вилкоксона—Вилкокс
- •1.2 Непараметрические критерии масштаба
- •1.2.1 Сравнение параметров масштаба двух совокупностей
- •1.2.1.1. Критерий Ансари—Бредли
- •1.2.1.2. Критерий Муда
- •1.2.1.3. Критерий Сижела-Тьюки
- •1.2.1.4. Критерий Кейпена
- •1.2.1.5. Квартальный критерий
- •2. Реализация непараметрических критериев в статистическом пакете r
- •2.1. Реализация критерия Манна-Уитни-Вилкоксона
- •2.2. Реализация критерия Крускала-Уоллиса
- •2.3. Реализация критерия Ансари-Бредли
- •2.4. Реализация критерия Муда
- •3. Исследования
- •3.1. Исследование распределения статистик рассматриваемых гипотез при "малых" и "больших" выборках
- •3.2. Исследование распределения статистик по критериям согласия Колмогорова и Смирнова
- •3. 3. Исследование асимптотических свойств рассматриваемых критериев
- •3.4. Эмпирическая мощность критериев
- •3.5. Реальные данные
- •Заключение
1.1.1.2. Быстрый (грубый) ранговый критерий
Рассматриваются
две выборки объемов
 и
и
 при
при
 (
( ).
Их
элементы ранжируются по возрастанию
совместно. Одинаковым наблюдениям
присваивается одинаковый усредненный
ранг. Для каждой группы находятся суммы
рангов
).
Их
элементы ранжируются по возрастанию
совместно. Одинаковым наблюдениям
присваивается одинаковый усредненный
ранг. Для каждой группы находятся суммы
рангов
 и
и
 и средние ранги
и средние ранги
 и
и
 .
.
Вычисляем
 .
Статистика -критерия может быть
аппроксимирована нормальным распределением
со средним
.
Статистика -критерия может быть
аппроксимирована нормальным распределением
со средним
 и дисперсией
и дисперсией
 .
.
Поэтому
при
 гипотеза сдвига отклоняется с доверительной
вероятностью α.
гипотеза сдвига отклоняется с доверительной
вероятностью α.
Эффективность критерия для нормально распределенных выборок 0,95 (для любого другого исходного распределения — не хуже 0,86).
1.1.1.3. Критерий Манна-Уитни-Вилкоксона
Пусть
 и
и
 - упорядоченные по возрастанию выборки.
Для проверки гипотезы сдвига Манн и
Уитни предложили ранговый критерий,
основанный на статистике [1]
- упорядоченные по возрастанию выборки.
Для проверки гипотезы сдвига Манн и
Уитни предложили ранговый критерий,
основанный на статистике [1]
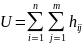 ,
где
,
где =
= (1.1)
(1.1)
Здесь
 - точное
число пар значений
и
,
для которых
- точное
число пар значений
и
,
для которых
 .
.
Если

 (1.2)
(1.2)
гипотеза
сдвига отклоняется ( - критические значения критерия
Манна-Уитни) [1].
- критические значения критерия
Манна-Уитни) [1].
С
 -статистикой
Манна-Уитни связана статистика Вилкоксона,
определяемая суммой рангов элементов
одной выборки (предположим,
объема
)
в общей упорядоченной последовательности
элементов совместной выборки объема
(
-статистикой
Манна-Уитни связана статистика Вилкоксона,
определяемая суммой рангов элементов
одной выборки (предположим,
объема
)
в общей упорядоченной последовательности
элементов совместной выборки объема
( )
[1]:
)
[1]:
 (1.3)
(1.3)
При
 применима аппроксимация [1]
применима аппроксимация [1]
 (1.4)
(1.4)
Статистика
W аппроксимируется нормальным
распределением, и гипотеза сдвига
отклоняется с достоверностью
 ,
если
,
если
 (1.5)
(1.5)
Если в двух сравниваемых выборках есть совпадающие значения, то им рекомендуется приписывать средние ранги (среднеарифметическое для каждой серии последовательных рангов). При этом в знаменателе статистики следует использовать величину [1]
 (1.6)
(1.6)
где
 — общее число групп совпадающих величин;
— общее число групп совпадающих величин;
 - число совпавших величин в i-й
группе (следует помнить, что совпадения
учитываются только тогда, когда совпавшие
величины принадлежат различным выборкам,
т. е. совпадения, целиком состоящие из
элементов одной и той же выборки, на
величину W не влияют).
- число совпавших величин в i-й
группе (следует помнить, что совпадения
учитываются только тогда, когда совпавшие
величины принадлежат различным выборкам,
т. е. совпадения, целиком состоящие из
элементов одной и той же выборки, на
величину W не влияют).
Более
точная аппроксимация предложена Иманом
[1]. В соответствии с ней гипотеза сдвига
отклоняется с достоверностью
 ,
если
,
если
 (1.7)
(1.7)
где
 (1.8)
(1.8)
 -
- квантиль нормального распределения;
-
- квантиль нормального распределения;
 -
- квантиль распределения Стьюдента с
-
- квантиль распределения Стьюдента с
 степенями свободы;
степенями свободы;
 .
.
Асимптотическая
эффективность критерия Манна—Уитни
равна

Одним из вариантов применения рассмотренного критерия является так называемый ранговый критерий Вилкоксона. Его статистика строится следующим образом. Для двух выборок и одинакового объема строится ряд разностей [1]
 (1.9)
(1.9)
который затем ранжируется по возрастанию.
В
упорядоченном ряду значений
 находится сумма рангов Т величин [1]
находится сумма рангов Т величин [1]
 .
(1.10)
.
(1.10)
Гипотеза сдвига отклоняется, если [1]

 ,
(1.11)
,
(1.11)
где
и
 - критические значения статистики Т
знакового рангового критерия Вилкоксона.
- критические значения статистики Т
знакового рангового критерия Вилкоксона.
При
 применимо приближение [1]
применимо приближение [1]
 (1.12)
(1.12)
При [1]
 (1.13)
(1.13)
гипотеза
сдвига отклоняется (здесь
 –
–
 -квантиль
стандартного нормального распределения).
-квантиль
стандартного нормального распределения).
Гипотеза
сдвига отклоняется на уровне достоверности
 если
[1]
если
[1]
 (1.14),
(1.14),
где
 (1.15)
(1.15)
 –
-
квантиль стандартного нормального
распределения;
–
-
квантиль стандартного нормального
распределения;
 -
-
квантиль распределения Стьюдента с
-
-
квантиль распределения Стьюдента с
 степенями
свободы.
степенями
свободы.
