Анализ времени

На рисунке 24 приведен полный сетевой график в формате ОУ, который является развитием простой логической диаграммы, представленной на рисунке 23. Названия работ и другие сокращения являются такими же, что и раньше.

Раннее начало каждой работы можно определить, двигаясь по графику слева направо. Всякое первое событие может начаться в момент t=0. В событии “слияния” (в точке схождения нескольких работ, например, событие 12) используется самое позднее завершение из входящих в него работ. Раннее начало события “разветвления” (например, событие 6, от которого ответвляются пять последующих событий) формирует раннее начало последующих событий (7 - 11).

Позднее начало каждой работы можно определить, двигаясь по графику справа налево. Раннее начало последнего события сети часто используется как позднее начало этого события. В событии “слияния” (например, событие 6) используется самое раннее завершение из входящих в него событий.

Сначала мы совершает по сети прямой проход, двигая слева направо. Работе 1 задается начальная дата недели 0.

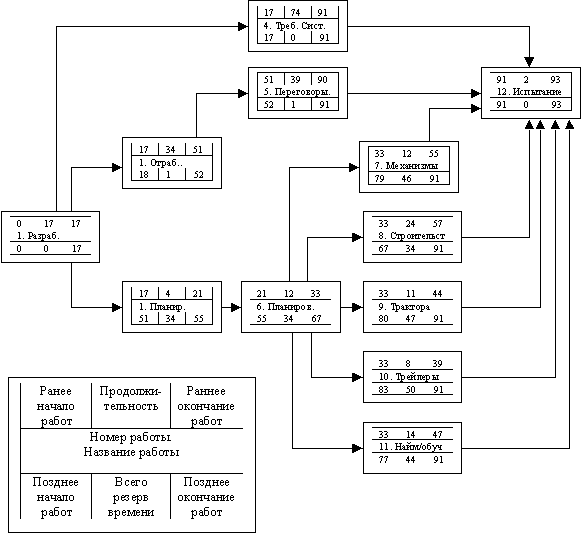
Рисунок 24. Новая организация материально-технического снабжения. Диаграмма предшествования.

Тогда раннее окончание - неделя 17, потому что продолжительность работы - 17 недель. Тогда ранним началом работы 2 тоже будет неделя 17. Работа 5 начинается в 17 + 34, продолжительность работы 2. Работа 4 выполняется параллельно с работой 2 и может начаться одновременно с ней. И так далее по прямому проходу до работы 12. В данной точке сливаются семь работ, поэтому мы должны использовать в качестве раннего завершения время той работы, которая завершится раньше других. И это будет ранним завершением работы 12. Это значение равно 91 (ранее завершение работы 4). Поскольку продолжительность работы 12 две недели, то раннее завершение всей сети будет равно 93 недели.

Теперь мы проделаем обратный проход, положив, что позднее завершение также равно 93 неделям (нижнее правое значение работы 12). Это означает отсутствие резерва времени, то есть разница между самой ранней и самой поздней датой работы равна нулю. Поэтому, поздним началом также является неделя 91, что влияет на работы с 7 по 11, у которых неделя 91 является поздним завершением. Разница между неделей 91 и ранними завершениями данных работ означает наличие резерва по каждой работе, то есть, что они могут начаться позднее, чем указано датами раннего начала. На обратном проходе, работа 6 является событием слияния работ 7 - 11. Возьмите самое раннее начало этих работ, т.е. неделю 67 в качестве позднего окончания работы 6. Если все сделано правильно, то у работы 1 также не будет резерва времени. То есть этот резерв будет равен нулю. Таким образом, критический путь сети - это линия, соединяющая работы с минимальным резервом - работы 1, 4 и 12.

Метод планирования и управления проектами (ПЕРТ)

Метод планирования и управления проектами, получивший известность как ПЕРТ, был разработан при выполнении проекта в интересах военно-морского флота США. Первым успехом было завершение программы создания ракеты “Поларис” в 1958 году, на два года раньше срока. Наиболее значимых результатов ПЕРТ достиг в военных и космических проектах, для которых характерна высокая степень неопределенности. По этому методу, продолжительность работы и бюджет проекта не являются раз и навсегда заданными (фиксированными), и для оценки можно применять теорию вероятности, как это было показано на рисунке 8.

В таких сетях продолжительность работы оценивается на оптимистичной, наиболее вероятной и пессимистичной основе, как показано на рисунке 25. Если оценки времени соответствуют бета распределению вероятности, то это означает, что разброс можно вычислить следующим образом:

t_e = t_o + 4t_l + t_p,

                   6

Где

t_e - Ожидаемое время работы

t_o - Оптимистическое время работы

t_l - Наиболее вероятное время работы

t_p,- Пессимистическое время работы

Дисперсия распределения (V) может быть рассчитан следующим образом:

Р аспределение во времени любого пути по сети будет иметь среднее значение, равное сумме средних значений работ пути, и дисперсию, равную сумме дисперсий. См. рисунок 25.

С реднее первой работы

 

Д исперсия первой работы

С реднее второй работы

 

Д исперсия второй работы

С реднее значение дисперсии сети

Д исперсия распределения сети

Полагается, что распределение на всем пути сети будет нормальным распределением.

Преимущество этой дополнительной информации заключается в том, что мы можем изучать “рискованность” каждого пути по сети, а также его длительность.

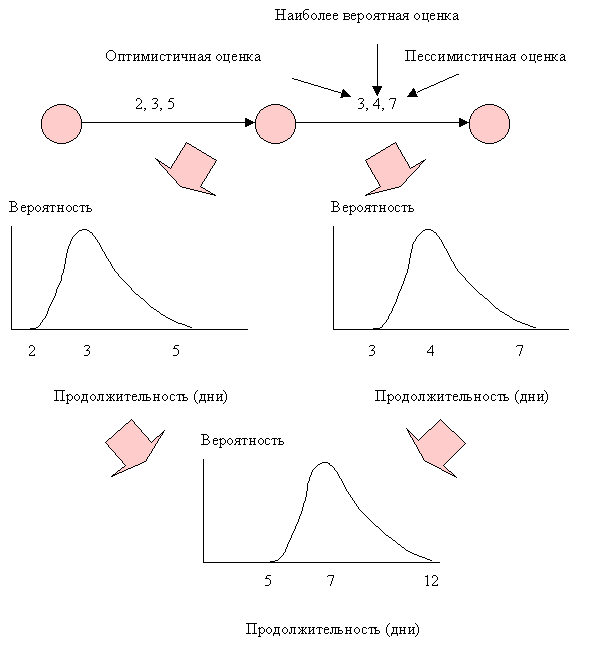
Рисунок 25. Суммирование вероятностной оценки времени для определения продолжительности выполнения всего проекта

Например, на рисунке 26 показана простая сеть, состоящая из двух путей. Верхний путь является критическим, распределение его длительности равно 10,5 с дисперсией 0,06 (поэтому стандартное отклонение равно 0,245). Средняя величина распределения некритического пути равна 9,67, а дисперсия 0,66 (поэтому стандартное отклонение равно 0,812). Суть происходящего состоит в наличии у некритического пути шансов на деле превратиться в критический. Хотя мы не будем здесь вдаваться в подробности вероятностных расчетов, можно определить вероятность превращения любого подкритического пути в критический при фактическом выполнении проекта. На практике, даже если вероятностные расчеты считаются не стоящими усилий, полезно хотя бы примерно оценивать рискованность каждой части сети.

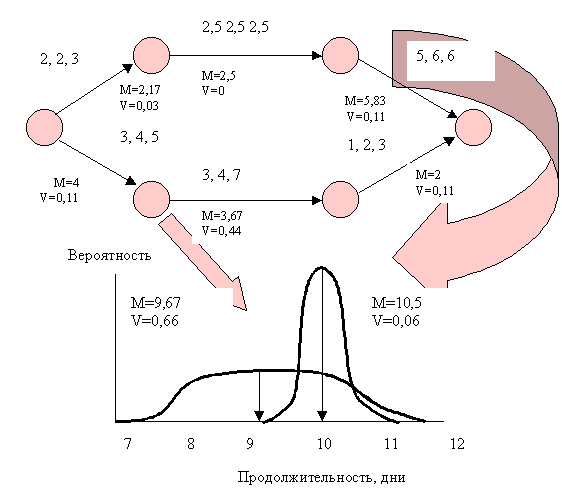
Рисунок 26. Один путь сети может иметь самую большую продолжительность, а другой – наибольшее отклонение

Ограничения на ресурсы

Как было показано выше, управляющая сетевыми взаимоотношениями логика берет свое начало в технических деталях проекта. Но на эти отношения между работами могут накладывать свои ограничения и ресурсы. На рисунке 27 показана простая сеть из двух путей, на которой показаны как продолжительность каждой работы, так и количество занятых на ее выполнении сотрудников. Показан и сводный график ресурсов, на котором представлены три работы критического пути (а), (с), (е). Все другие работы имеют некоторый резерв времени, следовательно, могут выполняться гибко.

Некритические работы на графике ресурсов начинаются так рано, как это только возможно. В результате профиль ресурсов меняется от семи до трех занятых. Но даже при наличии семи работников, руководитель проекта может пожелать выровнять нагрузку для организационного удобства. Если работников меньше семи, то проект должен быть перепланирован. Положим, у нас имеется только пять человек. Проект все еще можно завершить в те же сроки, что и показано на рисунке 28. Работа (b) может быть выполнена только после завершения работы (а). Профиль ресурса (а) получается таким, что количество занятых колеблется между четырьмя и пятью работниками, но находится в пределах заданного количества в пять человек.

Однако, для достижения этого необходимо потребовать, чтобы работа (b) началасть только после завершения работы (а). В этом заключается логическое ограничение, которое, если мы его применим, изменит сеть так, как это показано на рисунке 28. В этой сети все работы являются критическими, что и видно из графика ресурсов.

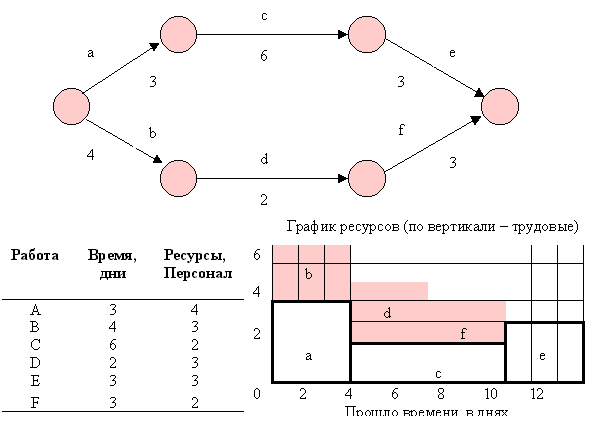
 Рисунок 27. Профиль ресурсов сети, с учетом того, что работы начинаются как можно раньше

Сокращение сетей по времени

Сокращение сетей есть процесс уменьшения временных интервалов по работам критического пути в целях досрочного завершения проекта. Обычно такая “сокращательная деятельность” подразумевает дополнительные затраты. Увеличение затрат объясняется следующими причинами:

• Сверхурочная работа.

• Дополнительные ресурсы, например, трудовые ресурсы.

• Субподрядные работы.

На рисунке 29 показан пример сокращения простой сети. По каждой работе вместе с ее нормальной продолжительностью и нормальными затратами указываются сниженная продолжительность и увеличенные затраты. Не все работы могут быть сокращены по срокам. Например, ничего нельзя сделать с работой (е). Критический путь определяется работами (а), (b), (с) и (е). Если совокупное время проекта будет снижено, должна быть сокращена продолжительность одной из работ критического пути. Для того, чтобы определить, какую работу нужно сократить, по каждой работе рассчитывается “наклон кривой затрат”. Это затраты за период меньшей продолжительности. Самым экономичным способом сокращения сроков выполнения всего проекта будет уменьшение продолжительности выполнения той работы, кривая затрат которых имеет наименьший наклон. В нашем примере такой работой является работа (а), сокращение которой будет стоить 2000 долларов и сократит продолжительность проекта на одну неделю.

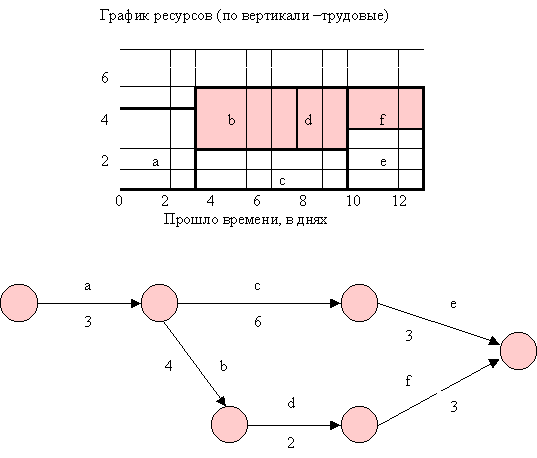
 Рисунок 28. Профиль ресурсов сети, с некритическими работами, отложенными по причине нехватки ресурсов. В этом случае логика сети изменяется, чтобы все работы были критическими

После этого может быть сокращена продолжительность работы (с), что позволит сэкономить еще две недели, но будет стоить дополнительно 5000 долларов. В этот момент все работы становятся критическими и дальнейшая экономия времени может быть достигнута за счет сокращения одновременно двух работ.

Кривая времени-затрат, приведенная на рисунке 29, является типичной кривой. Первоначальная экономия достигается сравнительно дешевым способом, если будет сокращена продолжительность работ с минимальным наклоном кривой затрат. Далее сокращаются более дорогие работы, в конце концов совместно критическими становятся несколько работ. В этой точке неизбежно экономия по времени может быть достигнута только за счет параллельного сокращения продолжительности нескольких работ.

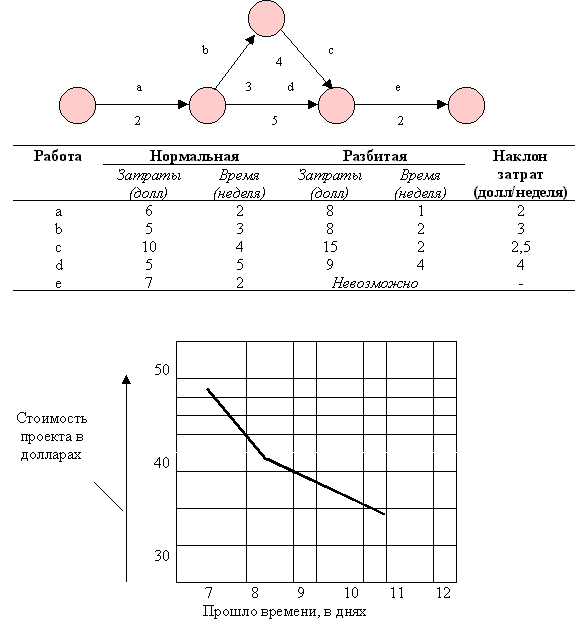
Рисунок 29. Разбивка работ для сокращения сроков проекта становится все более дорогой