7.Зважені графи і алгоритм пошуку найкоротшого шляху.
8. Орієнтовані графи і дерева.
Часто доводиться розглядати графи з орієнтованими ребрами, тобто ребрами, для яких вказані початок і кінець. Прикладами таких графів є мережі автомобільних доріг з однобічним рухом або схеми програм для ЕОМ. Недостатньо простих (неорієнтованих) графів і для опису несиметричних стосунків. Прикладами подібних стосунків може служити порядок виконання комплекса робіт, що задається за допомогою мережевого графіка або турнірна ситуація в спортивних змаганнях.
Хай V- кінцева непорожня безліч, V2 — декартовий квадрат. Орієнтований граф
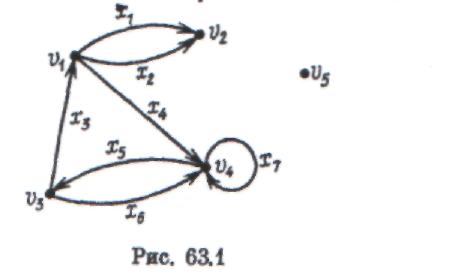
(орграф) - це пара (V, А), де А V2 . Елементи безлічі V називаються вершинами орграфа G - (V, А), а елементи безлічі А — його дугами. Таким чином, дуга - це впорядкована пара вершин. Безліч вершин і дуг орграфа G позначається через VG і AG відповідно. Число \VG\ називається порядком орграфа G і позначається через \G\. Якщо х - (і, v) — дуга, то вершини и і v називаються її кінцевими вершинами, причому и називається початком дуги х, a v — кінцем. Говорять, що дуга інцидентна кожній зі своїх кінцевих вершин. Говорять також, що дуга виходить зі свого початку і заходить в свій кінець. Дуга із співпадаючим початком і кінцем, тобто дуга вигляду (v, V), називається петлею. Можна визначити орієнтовані графи з декількома дугами, що мають загальний початок і загальний кінець (мультиграфи). Такі дуги називаються паралельними. На малюнку дуга зображається направленою лінією, що йде від початку дуги до кінця. Напрям лінії позначається стрілкою. Наприклад, для графа G, представленого на мал. 63.1, VG = (vl, v2, v3, v4, v5 ), AG ={xl, x2, хЗ, х4, х5, хб, x7}, причому xl і x2 —паралельні дуги, а х7 - петля. Вершини орграфа називаються суміжними, якщо вони є кінцевими для деякої дуги. Дуги називаються суміжними, якщо вони мають загальну кінцеву вершину.
Хай G - деякий орграф. Орієнтованим маршрутом (або просто маршрутом) в графові G називається:
така послідовність S - (vO, xO,vl, x2 ..., хп, vn) (1) його вершин vі і дуг xj що чергуються, що Хі = {Vi-l, Vi) (і= 1, п). Такий маршрут назвемо (vO, vn) -маршрутом. Вершини vO і vn назвемо крайніми, а решта вершин маршруту (1) -проміжними (внутрішніми). Довжиною маршруту називається число вхідних в нього дуг. Маршрут називається ланцюгом, якщо всі вхідні в нього дуги різні, і шляхом, якщо всі вхідні в нього вершини, окрім, можливо, крайніх, різні. Якщо в орграфі G немає паралельних дуг, то маршрут (1) може бути заданий послідовністю вхідних в нього вершин: S = (vO, v1..., vn). В будь-якому разі маршрут можна задати послідовністю вхідних в нього дуг: S = (хі, х2 ..., хп). Маршрут називається циклічним, якщо його перша і остання вершини збігаються. Циклічна дорога називається контуром. Вочевидь, що будь-який (и, v) -маршрут при и v містить (и, v) —маршрут, а при и = v — контур. Послідовність (1) вершин, що чергуються, і дуг графа G, таких, що
Хі = (vі-1, vi) або Хі = (vi, vі-1), називається напівмаршрутом. Аналогічно визначаються напівланцюг, напівшлях і напівконтур.
Якщо в орграфі існує (и, v) — маршрут, то говорять, що вершина v досяжна з вершини и. Будь-яка вершина вважається досяжною з самої себе. Орграф називається сильним (або сильносвязним), якщо будь-які дві його вершини досяжні одна з одною. Орграф називається однобічним (або однобічно-зв'язковим), якщо для будь-якої пари його вершин щонайменше одна досяжна з іншої. Орграф називається слабким (слабосвязним, зв'язковим), якщо будь-які дві його вершини сполучені напівмаршрутом.
Оскільки будь-яка вершина графа досяжна з себе, то одновершинний граф одночасно і сильний, і односторонній, і слабкий.
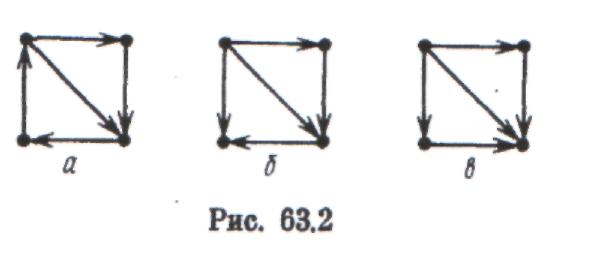
Вочевидь також, що будь-які дві неспівпадаючі вершини сильного орграфа належать деякому циклічному маршруту.
На мал. 63.2, а зображений сильний орграф, на мал. 63.2, б — односторонній, а на
мал. 63.2, в — слабкий.
Маршрут, що містить всі вершини орграфа G, називаєтся остовним.
Твердження 63.1. Орграф є сильним тоді і лише тоді, коли в нім є остовний
циклічний маршрут.