3. Булеві функції. Властивості функцій алгебри логіки. Реалізація булевих функцій формулами.

План.

1. Вступ.

2. Основні поняття та означення.

3. Способи задання булевих функцій.

4. Область визначення булевої функції.

5. Булевий простір.

6. Повнота системи функцій.

1.Онови математичної логіки покладено в працях англ. математика Джорджа Буля (1815-1864), батька Етель Ліліан Войнич, Янз є автором книги "Овід". Це такі праці, як "математичний аналіз логіки" (1847) і "Закони мислення" (1854), де він вперше виклав алгебру логіки - алгебру Буля. її формули застосовані незалежно від того, що мати на увазі під літерами, які вживаються в алгебрі. В алгебрі Буля літери позначають висловлення , а всі правила звичайної алгебри залишаються без змін. Оскільки всі наші міркування складаються з висловлень або думок, булева алгебра є логікою, через що вона дістала назву алгебри логіки.

Буль запропонував у формулах літерами позначати не числа , а висловлення і показав , що можна так вибрати дії додавання та множення , щоб формули звичайної алгебри залишалися без змін. В алгебрі логіки висловлення поділяються не за їх змістом або значенням , а тільки відносно того , істинні воно чи хибні. Приймається , що кожне висловлення може бути істинним (1) або хибним (0).

2. Булеві функції належать до класу однорідних функцій. Це найпростіший і водночас найважливіший клас однорівних функцій, що використовуються для ЕОМ, а саме для перероблення дискретної інформації. Як моделі засобів перероблення застосовується поняття автомата. Для формального опису цифрового автомата слугує апарат алгебри логіки. Останню утворюють множини всіх булевих функцій разом з операціями заперечення , кон'юнкції, диз'юнкції, імплікації тощо.

Будемо розглядати функції f(х₁; х_2…x_n), аргументи визначено на

множині Е₂ = {0,1}, такі, що, f(x₁; x_2; х_п) є Е₂, коли x₁ є Е₂(і = 1,2.. п). Ці

функції називають булевими.

Логічними (булевими) змінними в булевій алгебрі називають величину які незалежно від їхньої конкретної суті можуть набувати лише двох значень 0 і 1.

Булавою, або перемикаючою, функцією f(x,;x₂. х_n-1), називають

функцію, яка, як і п її аргументів , може набувати лише двох значень : 0 або І.

двійковим поданням n- розрядного числа ( кількість додатніх n - розрядних чисел 2" ).

Булева ф-ція 2-ох аргументів є повністю визначеною, якщо задано її значення в кожному з 4-ох можливих наборів (2²=4); ф-ія 3-ох аргументів у восьми (2³ =8) наборах також буде повністю визначеною.

Теорема: Число f₂ (n) усіх функцій, що залежить від n змінних

X_1;x₂... x_n дорівнює 2².

Від 2-ох аргументів залежить 16 булевих функцій, від 3-ох -256, від 4-ох-65500.

Функції 2-ох змінних змінних відіграють важливу роль, тому що з них може бути побудована будь - яка булева функція.

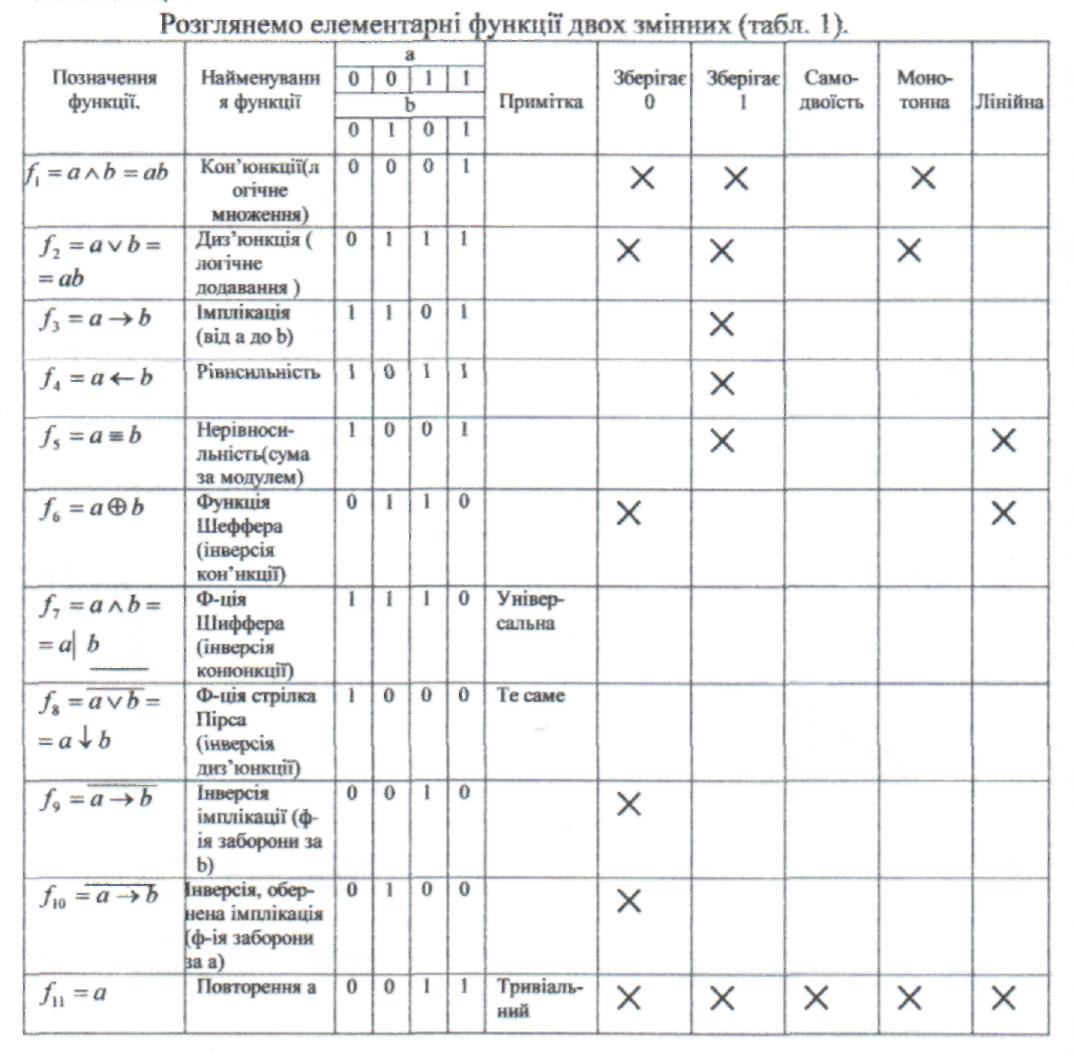
5. У математичній логіці часто вживається елементарні функції, які відіграють таку саму важливу роль, як, наприклад , х ⁿ або sin x у математиці.

6. Часто для спрощення запису булевої функції замість повного переліку термінів використовують двійкові запити наборів , для яких функція набуває одиничних значень. Наприклад, запис

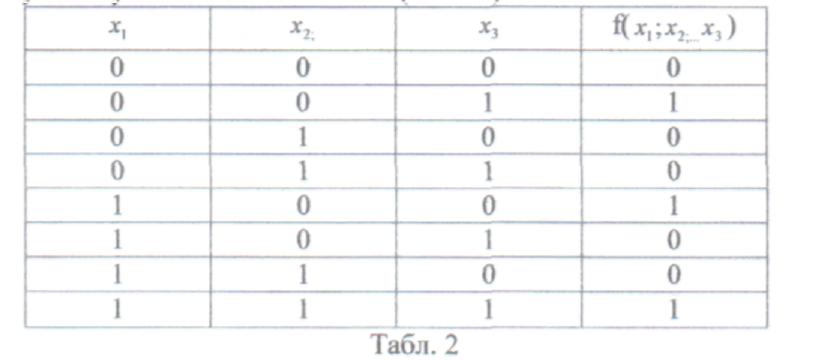
Означає що функція набуває одиничних значень на наборах 1,4,7, Таку форму запису називають числовою (табл. 2)

Булевим простором може бути названа множина всіх наборів булевих векторів: М.

Безпосередній перелік елементів функції можна здійснити за допомогою булевої матриці, кожен рядок якої задає один з елементів

7. Булеву функцію можна задати двома способоми - табличним формульним . Формула - більш компакний спосіб задання функції, однак вона задає функцію через іншу функцію. Тому формулу можна розглянути як систему функцій (елементарних). Для будь - якої системи

Система функцій Σ називається функціонально первинною