
- •Лабораторная работа №4
- •Донецк - 2003
- •I. Численные методы решения дифференциальных уравнений.
- •II. Методы Рунге - Куп а.
- •3. Модифицированный метод Эйлера.
- •III. Методы прогноза и коррекции.
- •Var X,XI,y,y1 : Ar; I : word;
- •6. Выводы, содержащие анализ точности и скорости сходимости рассмотренных методов.
Второй
результат (/г =
0.01)
данного метода удовлетворяет точности
решения исходного
уравнения по
отношению к эталонному результату.
Этот метод, как и предполагалось,
оказался
самым точным.
Один
из самых серьезных недостатков методов
Рунге - Купа
состоит в отсутствии про-
стых
способов оценки их ошибки.
для
i =
1,2,3,...
Итерационный
процесс прекращается, когда
для
некоторого £ >
0.
Листинг
программы и результаты расчета для
метода прогноза и коррекции при трех
раз-
личных величин шагов (для
вычисления yi
использован метод Рунге - Кутга второго
порядка -
исправленный метод Эйлера):
{ ЛАБОРАТОРНАЯ РАБОТА № 4.
"ЧИСЛЕННЫЕ
МЕТОДЫ"
Программа
№
5 : METHOD ADAMSA - BOSHFORA }
Program
lab_4_5;
Uses
Crt;
Отличительной
чертой методов Рунге - Кутта является
то, что при вычислении следую-
щей
точки хП1+1,
ут+]
используется информация только о точке
хт, ут
, но не о предыдущих.
Кроме
того, для методов Рунге - Кутта
отсутствуют достаточно простые
способы оценки ошибки, что
приводит
к необходимости рассмотрения некоторых
дополнительных методов решения
диффе-
ренциальных уравнений.
Отличительное
свойство этих методов, что с их помощью
нельзя начать решение уравне-
ния,
так как в них необходимо использовать
информацию о предыдущих точках решения.
Чтобы
начать решение уравнения, имея
только одну точку, определяемую
начальными условиями, или
для того,
чтобы изменить h
, необходим метод
типа Рунге - Кутта. Поэтому приходится
использо-
вать разумное сочетание
этих двух методов.
Методы,
один из которых будет рассмотрен ниже,
известны под общим названием мето-
дов
прогноза и корректировки. Как ясно из
названия вначале «предсказывается»
значение ym+i
, а
затем
используется то или иной метод его
«корректировки».
5.
Метод Адамса - Босфора.
Для
прогноза используем формулу второго
порядка:
[/» , = у +
2hf(x
,у
\
^
Jm+1 -’m-l V m,Jm/
где
(0) - означает
исходное приближение ym+i
, т.е. предсказанное
значение. Непосредст-
венно из
написанной формулы следует, что с ее
помощью нельзя вычислить
yi
, так как для
вы-
числения yi
потребовалась
бы точка, расположенная перед начальной
точкой уо .
Чтобы начать
решение с помощью метода
прогноза и коррекции, для нахождения
yi
необходимо использовать
метод Рунге
- Кутта.
Для
коррекции возьмем
формулу,
похожую на исправленный
метод Эйлера: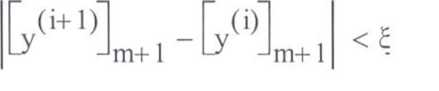
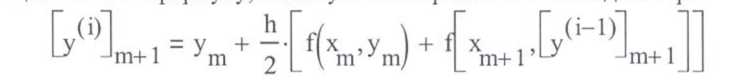
III. Методы прогноза и коррекции.
Const E
=
0.0001;
N_max
=
5 000;
X_beg
= 1 { переменная
X - начальное условие };
Y_beg
= 1 { переменная
Y -
начальное условие };
Х_коп
=8.5 { требуемое
конечное значение аргумента };
h =
0.1; { (h=0.1,0.01,0.005)
- величина шага
)
Type Ar
= array[0..N_max]
of real;
Y_kon,
Y_rez_l,
Y_rez_2 : real;
Function F (X, Y :real) :
real;
Begin
F:=
{2/(X*X*X)) - (3*Y)/X;
End {
F } ;
{
}
Function Fii (X, Y,
h :real) : real;
Var F_tool :
real;
Begin
F_tOOl:=F(X,
Y) ;
Fii :=
F(X+h/2,
Y+(h/2)*F_tool);
End {
Fii };
{
}
Begin
ClrScr;
X
10] :=
x_beg; Y[0]
:= Y_beg;
i:=0;
While X[i] <=
X_kon do
Begin
[i+1]:=Y[i]+h*Fii(X[i],Y[i],h); { модифицированный
метод }
inc(i); { Эйлера }
X[i] :=
X[i-1]+h
End;
Y_kon:=Y[i];
Repeat { цикл по верхнему индексу }
X
[0] :=X_beg;
Y[0]:=Y_beg;
Y_rez_l :=
Y_kon; i:=l;
While X[i] <=
X_kon do
Begin
X[i]:=X[i-1]+h;
[i]
:=Y [i-1]
+ (h/2)*(F(X
[i-1] , Y[i-1])
+ F(X
[i] ,Y [i])) ;
inc(i)
;
End;
Y_kon:=Y[i];
Y_rez_2 :=
Y_kon;
Until abs(Y_rez_2 - Y_rez_l) <
E;
Writeln(' ':15,'Step
= 1,h:l:3);
Writeln (' ':10,'Y_Result
= ',Y_rez_2:3:7);
Repeat
Until KeyPressed
End.
Результаты
работы
прог
раммы:
Step
= 0.1
Y_Rezult
= 0.0255086
Step =
0.05
Rezult =
0.0260630
Step =
0.005
Rezult =
0.0260238Var X,XI,y,y1 : Ar; I : word;
