


МИНИСТЕРСТВО
ОБРАЗОВАНИЯ
И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра
вычислительной техники
«Численное
интегрирование»
Выполнил:
студент гр. ВТ-01
аз
ИВАНИЦА
С.В.
Проверил:
КРАВЧЕНКО
АТ.
Лабораторная работа № 3
Донецк - 2003

Данная
лабораторная работа посвящена
вычислению определенного интеграла
различ-
ными численными методами.
Все они основаны на том, что интеграл
представляется в виде преде-
ла суммы
площадей, и позволяет вычислить эту
сумму с достаточной точностью.
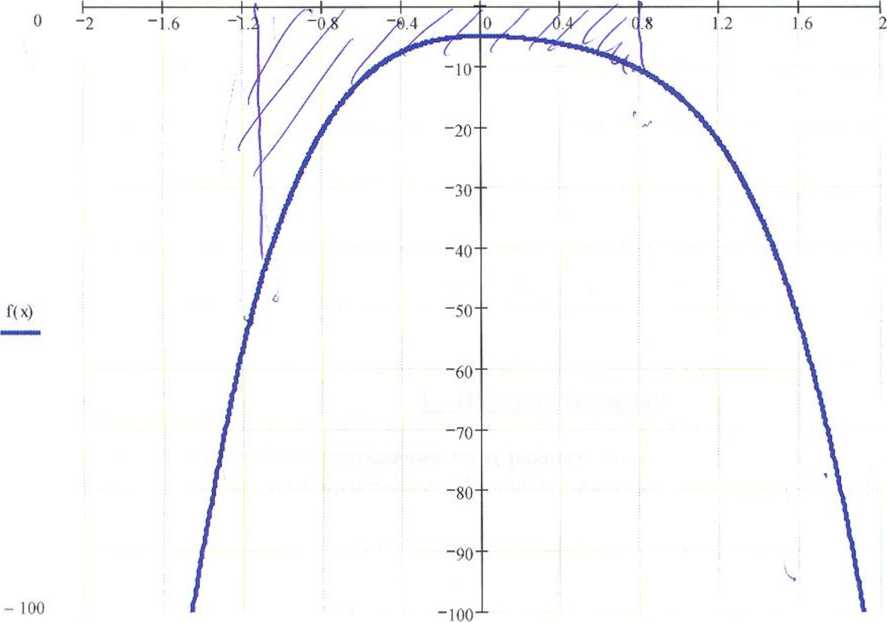
-2 х 2
Рис.1.
График
подынтегральной функции/(х)
на всей числовой прямой.
Перед
тем,
как начать решение интеграла численными
методами, произведем вычисление
значения
по правилам ВМ. Для более точного и
быстрого вычисления прибегнем к помощи
про-
фессионального математического
пакета MachCad
Professional.
Произведем
вычисление интеграла
символьным
методом. Это нам даст точное математическое
(не численное!) вычисление значения
с
помощью символьного процессора MachCad.
Конечно,
символьное интегрирование
возможно
только для небольшого круга
несложных подынтегральных функций, но
в нашем случае мы по-
лучили довольно
точный результат.
'°'8
(
\
\0.66-
cos(2.31
•
х) - 0.04-
ехр(-2.61-
х) - 9.58-
х4
+
9.4.
х3
- 8.96-
х
-
5.5lj
dx->
-21.9974707521255222е
-1.1
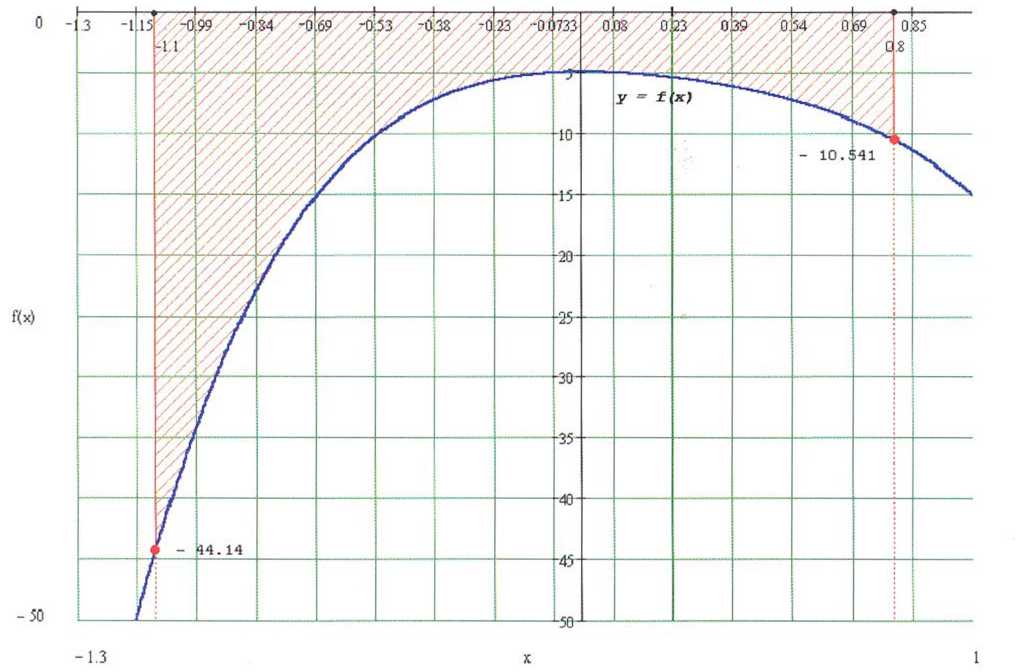
Определенный
интеграл I
представляет собой площадь (рис.2.),
ограниченную
кривой
f(x),
осью
х и прямыми х=а
и х=Ь
(в нашем случае а=-1.1,
Ь=0.8).
Будем вычислять интеграл (1)
,
разбивая
интервал от а
до b
на
множество меньших интервалов, находя
приблизительно площадь
каждой
полоски, получающейся при
гаком
разбиении, и суммируя площади этих
полосок.
Требуется
вычислить следующий определенный
интеграл:
Дх)
-0.66*cos(2.31*x)~0.04*е™*
-9.58*х4
+9.4*х3
-8.96*х2
-5.51;
График
функции f(x)
представлен
па рис.1.
![]()
Рис.2.
Графическое
изображение
исходного интеграла.
Разобьем
интервал интегрирования на п
равных частей,
каждая длиной h=(b-a)/n.
Рас-
смотрим
теперь один из этих интервалов. Площадь,
лежащая под кривой y=f(x),
между х,
и х,
ц
равна:
fxi+l
f(x)
dx
v
xi
Если
h достаточно мало, то эту
площадь без большой ошибки можно
приравнять к площади
трапеции:
1.
= —(у.
+ у. ,)
'
'+,>
(2)
Просуммировав
площади по всем п
интервалам, получим:
I
=
п-1
=£
i
= О
где
хо
= а>
х„ = Ъ.
Теперь,
подставляя (2)
в (3),
получаем:
h
1. Правило трапеций.
For |
n = 15 |
Integral = |
-22.16432 |
For |
n = 55 |
Integral = |
-22.05757 |
For |
n = 126
|
Integral = |
-21.99988 |
В
результате получили довольно
приблизительное значение, которое хоть
и сходится к по-
лученному ранее, но
при больших значениях п
(600...800), что
приводит соответственно к боль-
шому
количеству суммирующих циклов.
Этот
метод оказался не очень эффективным.
Чтобы
найти более точное значение интеграла,
рассмотрим более усовершенствованные
правила
и методы численного интегрирования.
Чтобы
найти более точное
значение интеграла можно воспользоватея
стравнительно
про-
стым усовершенствованным методом
трапеций.
Выберем
некоторую другую величину шага разбиения
к
=
(Ь-а)/т,
причем т<>п.
Если
4
-
значение интеграла, вычисленное по
павилу трапеций с шагом К
а Д
- значение
интеграла ,
вычисленное по правилу трапеций с шагом
к,
то лучшее приближение ,
чем Д
или h
получается
по формуле:
Вычисленное
таким образом значение интеграла I
является лучшим приближеием ,
чем //,
или
Д.
Если же вторая производная у
”(х)
действительно постоянна при
а<=х<=Ь,
то ошибка огра-
ничения в данной
формуле равна нулю. Этот метод впервые
был предложен Ричардсоном (1927г.).
Листинг
программы, производящей вычисление
значения определенного интеграла
по экс-
траполяционному
переходу к пределу, представлен ниже:
{ ЛАБОРАТОРНАЯ
РАБОТА № 3.
"ЧИСЛЕННЫЕ МЕТОДЫ"
"
Численное интегрирование"
Программа
№ 2 : EXTRAPOLYATSIONNY
PEREXOD
К
PREDELU
}
Program
lab_3_l;
Uses
Crt;
Const
n =
15 ;
m
=
2*n+50;
a
=
-1.1;
b
=
0.8;
Type
Ar =
array[0..N+M]
of real;
Var
X :
Ar;
step,
Ih,
Ik,
Integral,
k :
real;
i,
iter
:
byte;
{
}
Function
Func (X:real)
:
real;
Begin
Func:=
0.66*cos
(2.31*X)-0.04*exp(-2.61*X)-9.58*X*X*X*X
+
9.4*X*X*X
- 8.96*X*X-5.51;
End
{
Func };
{
}
Procedure
Made_Integr
(iter :
word);
{
процедура,
считающая интеграл по
правилу трапеции }
Begin
step:=(b-a)/iter;
X[0]:=a;
X[iter]:=b;
For
i:=l to iter-1 do X[i]:=X[i-l] +
step;
Integral:=
0.0;
For
i:=0
to iter-1 do
Intearal:=
Integral
+
(step/2)*(Func(X[i]}
+
Func(X[i+1]));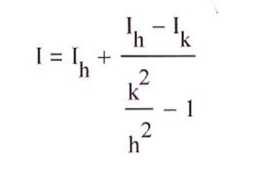 (4)
(4)
