
- •1. Машинобудування — провідна галузь народного господарства України.
- •2.Основні проблеми дисципліни тмм.
- •3.Історія розвитку тмм.
- •6.Визначення:механізму і машини.
- •7. Кінематичні пари та їхня класифікація.
- •9.Кінематичні та їх класифікація.
- •13.Класифікація механізмів.
- •12. Групи Ассура та їхня класифікація.
- •16. Синтез кривошипно повзунного механізму.
- •20.Функції переміщення вхідних ланок важ.Мех
- •32. Закони руху веденої ланки.
- •34.Кінематичний аналіз мех метом планів.
- •35.Кінематичний аналіз мех метом діаграм.
- •46. Поняття про евольвента кола.
- •39. Кут тиску та кут передачі руху в кулачкових мех.
- •47.Властивості евольвенти кола.
- •48. Основні розміри циліндричних зубчастих коліс.
- •49.Поняття про кола зубчастого колеса(визна).
- •50. Геометрія евольвентного зачеплення(якісні хар).
- •51. Косозубі циліндричні колеса. Основні параметри,їх переваги та недоліки.
- •Конічна зубчаста передача
- •Косозубе колесо.
- •Форми і методи наукового пізнання.
- •66. Тертя в: цапфі, п'яті.
- •82. Зведені сили і моменти.
- •68.Тертя кочення у вищих кінематичних парах.
- •87. Зрівноважування тіл обертання.
- •80. Теорема м.Є. Жуковського.
- •89. Статичне і динамічне балансування тіл обертання.
- •88.Рівняння руху амортизованого об'єкта
- •Розкрийте сутність естетики як типу духовності.
- •Назвіть і охарактеризуйте основні категорії естетики.
- •Етика: її предмет, зміст та основні категорії.
- •Етика як практична філософія.
Незрівноваженість
тіл обертання, яка викликана недосконалістю
техно-логічного процесу їх виготовлення,
усувається шляхом прибавлення або
видалення невеликої маси матеріалу.
Виправлення такої незрівноваженості
називається балансуванням.Незрівноваженість,
яка виникає внаслідок конфігурації
деталі /колінвал, кулачок/ усувається
шляхом встановлення противаг.Нехай
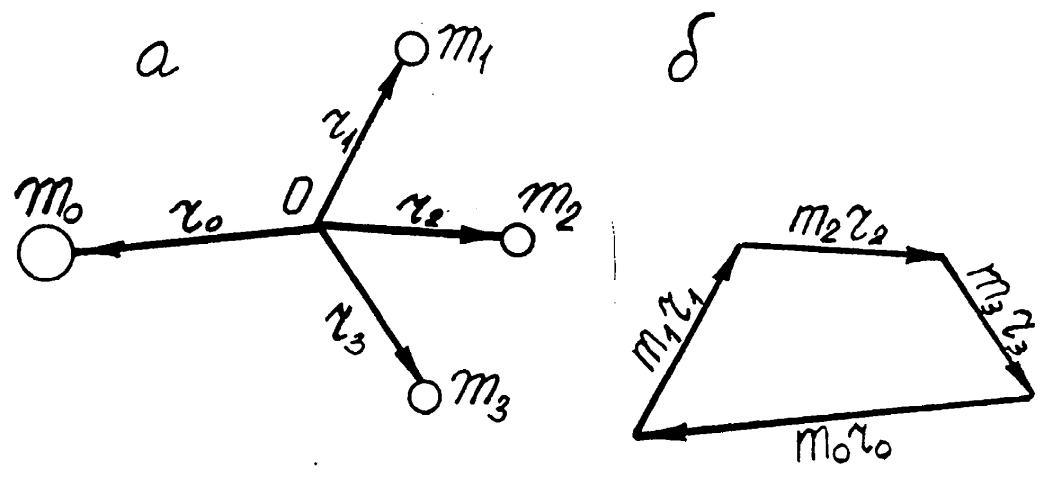
потрібно зрівноважити три маси, що
обертаються на валу і центри мас яких
розміщені в одній площині /рис. 8.1, а/. В
цьому випадку достатньо підібрати
четверту масу так, щоб центр її мас
також знаходився в цій же площині, а
радіус-вектор загального центру мас
дорівнює нулю rS
= 0.
Відстані центрів мас т1,
т2,
т3
і т0
до осі обертання позначимо r1,
r2,
r3
i
r0.
Зрівноваження
противагою Відцентрові
сили інерції кожної маси дорівнюють:
Для
зрівноваження необхідно, щоб головний
вектор сил інерції дорівнював нулю
Це
і є умова статичного зрівноважування
обертових тіл. Задача
вирішується графічним складанням
векторів тіri.
/рис.8.1,б/.
При
цьому вектор moro
показує напрям радіуса-вектора, на
якому потрібно встановити противагу,
задаючись величиною радіуса ro,
знайдемо масу противаги ro.
87. Зрівноважування тіл обертання.
![]() ,
,
![]()
![]() = 0, тобто
= 0, тобто![]() або
враховуючи
або
враховуючи
![]() .
.
Якщо
площину кріплення противаги конструктивно
не можливо вибрати в тій же площині
обертання що і незрівноважені маси, то
встановлюють дві противаги в двох
перпендикулярних, до осі обертання,
площинах /рис.8.2/. При
цьому необхідно виключити можливість
виникнення додаткових зусиль на
підшипники не тільки від результуючої
сили інерції, а і від моментів пар сил
інерції. Складемо
рівняння моментів:
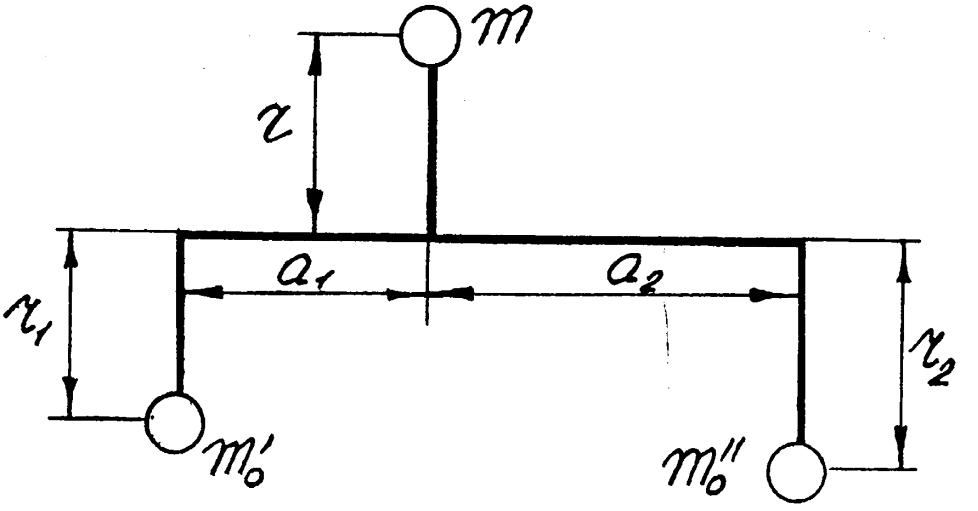
Зрівноваження
двома противагами Встановленням
двох противаг масами mo`
i
mo``
досягається повне зрівнова-жування
маси m,
при цьому необхідно, щоб центри мас m,
mo`
i
mo``
знаходи-лися в одній площині, яка
проходить через вісь обертання.
86.Визначення
геометричних розмірів маховика.
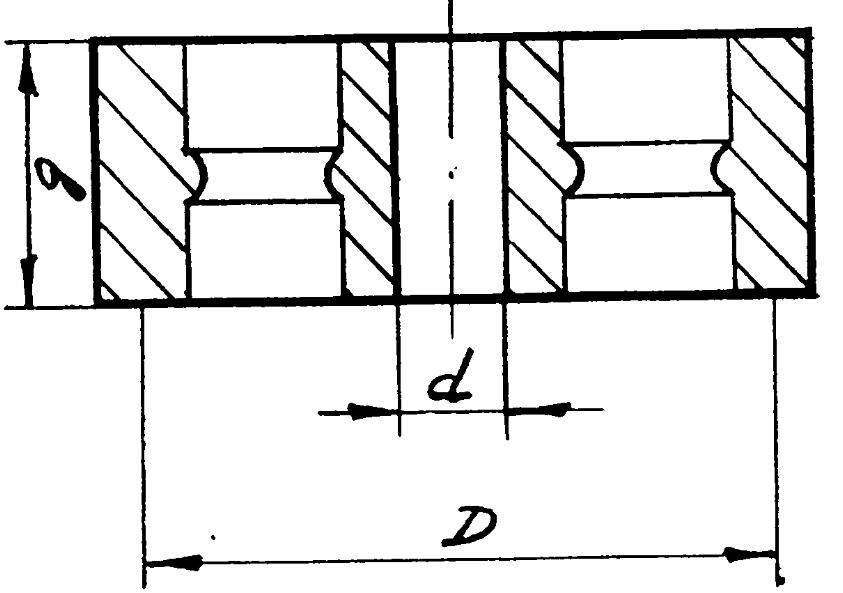
Визначимо геометричні розміри
маховика.Вважаємо, що маса маховика
рівномірно розподілена по колу діаметра
D,
а також нехтуємо моментами інерції
маточини і спиць, оскільки вони відносно
невеликі /рис.7.7/. Момент інерції
Якщо
врахувати моменти інерції маточини і
спиць, то:
Inmax
= 1.1 Imax
Вираз тD2
називається
маховим моментом, або характеристикою
маховика. Задаючись діаметром D
маховика, величина якого визначається
з конструкт-тивних міркувань, можна
легко визначити масу маховика. Щоб
запобігти небезпеці можливого розриву
маховика, його діаметр вибирають
таким, щоб колова швидкість на ободі
не перевищувала допустимої, для
матеріалу маховика величини. Наприклад,
для чавунного маховика допустима
швидкість V
= ЗО м/с. Якщо
маховик встановити не на вхідній ланці
механізму, а на якій-небудь і-й його
ланці, то з умови рівності кінетичних
енергій маємо:
![]()
![]() можна
подати так:
можна
подати так:![]() Ескіз
маховика.
Ескіз
маховика.
![]() ,
звідки:
,
звідки:
![]()
Якщо
між вхідною ланкою і двигуном встановлено
редуктор з передаточним числом UР
, то момент інерції маховика на валу
двигуна буде:
Необхідна,
потужність двигуна на вхідній ланці:
Nдв
= Mp
* ωcp,
/ де
Мр
= у * μМ. Механізм
з маховиком при усталеному русі працює
таким чином. В тих положеннях механізму
/в більшості при холостому ході/, коли
момент рушій-них сил більший за
момент сил опору /Мр>Моп/
збільшується кутова швидкість
вхідної ланки і тоді, маховик, завдяки
своєму значному динамічному моменту
інерції, сприймає надлишок кінетичної
енергії механізму і не дозволяє кутовій
швидкості надмірно зростати. В положеннях
механізму /в більшості при робо-чому
ході/, коли момент сил опору більший за
момент рушійних сил /
Моп
>Мр
/,
маховик віддає накопичену кінетичну
енергію, протидіючи зменшенню кутової
швидкості вхідної ланки. Отже, призначення
маховика - це регулювання в зада-них
межах періодичних коливань кутової
швидкості вхідної ланки механізму при
усталеному русі. Крім того, маховик
дозволяє зменшити потрібний рушій-ний
момент, а значить зменшити і необхідну
потужність двигуна.
85.Визначення
динамічного моменту інерції маховика.
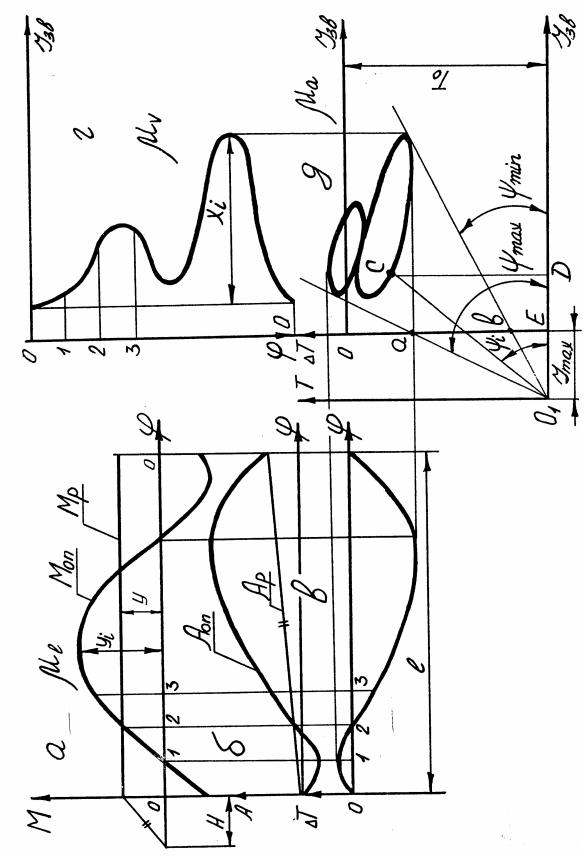
Визначимо динамічний момент інерції
маховика Imaх.
із рис.7.6,д:
Imax
= O1E
* μIзв
Таким
чином, вимірюючи в міліметрах
безпосередньо із рис.7.6,д відрізок
01Е
за формулою /7.28/ визначимо динамічний
момент інерції маховика. Проте при
малому значенні коефіцієнта
нерівномірності δ
точка перетину О1
дотичних може вийти за межі рисунка.
Значно простіше користуватися
відрізком ав.
Із рисунка видно, що: aE
= O1Etgψmax
i
bE
= O1Etgψmin. Віднімемо
від першого рівняння друге, отримаємо:
aE
– bE = O1E(tgψmax
– tgψmin).
/ Із
відношення
/7.15/ знаходимо:
Підставимо
значення
ψmax
і
ψmin.
із
/7.27/
і
0ІЕ
із
/7.28/ в
формулу
/7.16/, отримаємо:
![]()
![]()
 Звідки
знаходимо:
Звідки
знаходимо:
Нехай
в точці j
ланки АВ
прикладена сила Fj
/рис.7.З,а/. Перенесемо цю силу паралельно
їй самій в однойменну точку j
/ повернутого на 90° плану швидкостей
ланки /рис.7.З,б/.
Із
повернутого плану швидкостей потужність
Nj
сили можна визначити так:
де
hj
- перпендикуляр, опущений із полюса PV
плану швидкостей на лінію дії сили
Fi;
αj
- кут між вектором швидкості
а
- ланка механізму; б - повернутий план
швидкостей
Рис.7.3. Застосуємо
рівняння /7.11/ для всіх сил
що
і є доведенням теореми.
![]()
![]() і плечем hj.
і плечем hj.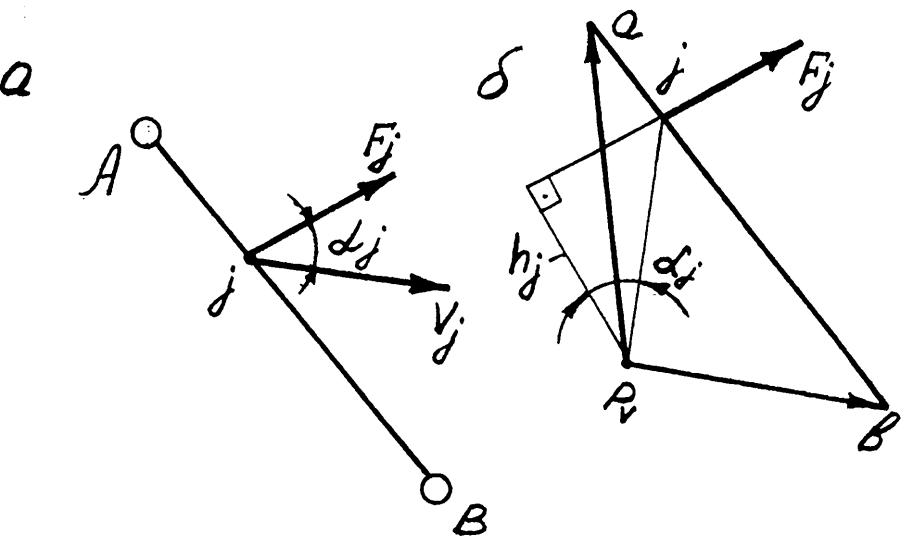
![]() /7.12/
/7.12/
