
- •Задача 5. МногоФакторный эксперимент а. Многофакторное уравнение регрессии первого порядка
- •5.3. Проверка многофакторного уравнения регрессии первого порядка на адекватность.
- •Б. Многофакторное уравнение регрессии второго порядка
- •Типовая задача (уравнение регрессии первого порядка)
- •3.2. Выполним предварительную обработку экспериментальных данных (внести в таблицу 3).
- •4. Создадим матрицу моделирования для построения двухфакторного уравнения регрессии первого порядка на базе цпфп (таблица 4) (раздел а, п. 5).
- •4.3. Проверим полученное двухфакторное уравнение регрессии первого порядка на адекватность по критерию Фишера (результаты расчета внесем в таблицу 4):
- •План решения типовой задачи (уравнение регрессии второго порядка)
- •Решение задачи по плану
- •2.4. Проверим полученное ортогонализированное двухфакторное уравнение регрессии второго порядка на адекватность по критерию Фишера:
- •Формулировки 30 вариантов контрольных задач
4.3. Проверим полученное двухфакторное уравнение регрессии первого порядка на адекватность по критерию Фишера (результаты расчета внесем в таблицу 4):
Рассчитаем параметр
в каждом опыте
по двухфакторному
уравнению регрессии первого
порядка. Например:
![]() .
.
Образуем столбец , и рассчитаем его значения. Например:
![]() .
.
Рассчитаем остаточную сумму квадратов
![]()
![]() ;
;
Рассчитаем и её число степеней свободы (см. уравнения (24) – (25)):
![]() ;
;
![]()
![]() .
.
Проверим полученное двухфакторное уравнение регрессии на адекватность по критерию Фишера:
‑ экспериментальное
значение критерия
Фишера
![]() (см. уравнение (26)):
(см. уравнение (26)):
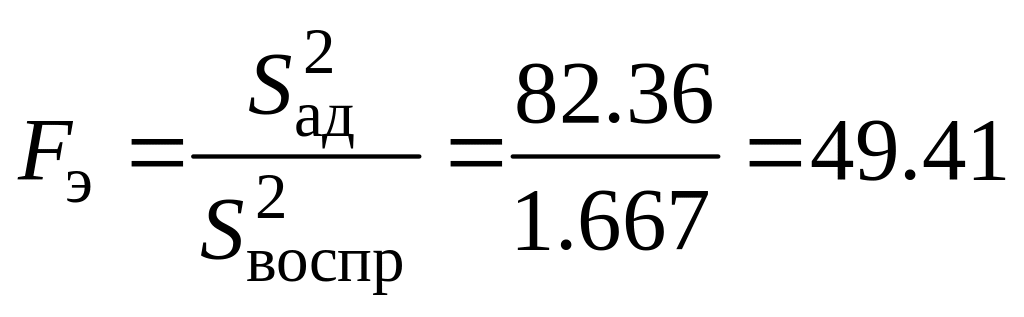 ,
так как
,
так как
![]() ;
;
‑ табличное
значение критерия Фишера
![]() при числах степеней свободы
при числах степеней свободы ![]() ,
,
![]() и доверительной вероятности р = 0.95
выбираем из таблицы Приложения 4:
и доверительной вероятности р = 0.95
выбираем из таблицы Приложения 4:
![]() .
.
Вывод: полученное
двухфакторное
уравнение регрессии первого
порядка
неадекватно,
так как
![]() (см. уравнение (28)).
(см. уравнение (28)).
5. Так как полученное уравнение регрессии первого порядка неадекватно, следует перейти к построению двухфакторного ортогонализированного уравнения второго порядка.
План решения типовой задачи (уравнение регрессии второго порядка)
1. Создать матрицу планирования для построения ортогонализированного двухфакторного уравнения регрессии второго порядка на базе ОЦКП и выполнить предварительную обработку экспериментальных данных.
2. Создать матрицу
моделирования
для построения ортогонализированного
двухфакторного
уравнение
регрессии
второго порядка,
рассчитать коэффициенты
![]() и произвести
статистическую оценку качества
полученного
уравнения
регрессии
(значимость
коэффициентов регрессии, адекватность
уравнения регрессии).
и произвести
статистическую оценку качества
полученного
уравнения
регрессии
(значимость
коэффициентов регрессии, адекватность
уравнения регрессии).
3. Найти оптимальные значения факторов, при которых параметр Y достигает максимальной величины, а также её абсолютную и относительную погрешность.
4. Принять решение о дальнейшем пути исследования изучаемого объекта.
Дополнительные
экспериментальные данные по урожайности
пшеницы (
)
на базе ОЦКП с числом опытов
![]() и числом дублей
для звёздных опытов (№№ 6 – 9)
представлены в таблице 5.
и числом дублей
для звёздных опытов (№№ 6 – 9)
представлены в таблице 5.
Таблица 5. ‑ Экспериментальные данные для звёздных точек ОЦКП
N2 |
|
|
|
|
|
|
6 |
– |
0 |
56 |
58 |
57 |
57 |
7 |
+ |
0 |
49 |
50 |
48 |
51 |
8 |
0 |
‑ |
40 |
45 |
42 |
45 |
9 |
0 |
+ |
56 |
57 |
55 |
58 |
Решение задачи по плану
1.
Создадим матрицу
планирования (таблица
6) (см. раздел Б,
п. 9), дополнив матрицу
планирования
(таблица 3) звездными точками
![]() .
Для
.
Для
![]() (см. уравнение (30)). Количество опытов
ОЦКП равно
(см. уравнение (30)). Количество опытов
ОЦКП равно
![]() ,
количество дублей
.
Внесём в матрицу
планирования
(таблица
6) экспериментальные данные из таблицы
2
и
дополнительные экспериментальные
данные для звёздных опытов из таблицы
5.
,
количество дублей
.
Внесём в матрицу
планирования
(таблица
6) экспериментальные данные из таблицы
2
и
дополнительные экспериментальные
данные для звёздных опытов из таблицы
5.
Таблица 6. ‑ Матрица планирования на базе ОЦКП для k = 2 и
результаты предварительной обработки
N |
|
|
|
|
|
|
|
|
|
|
1 |
‑ |
– |
1 |
1 |
46 |
44 |
45 |
45 |
45.00 |
0.6667 |
2 |
+ |
– |
3 |
1 |
35 |
38 |
36 |
35 |
36.00 |
2.000 |
3 |
‑ |
+ |
1 |
3 |
55 |
58 |
57 |
58 |
57.00 |
2.000 |
4 |
+ |
+ |
3 |
3 |
48 |
51 |
49 |
50 |
49.50 |
1.667 |
5 |
0 |
0 |
2 |
2 |
52 |
55 |
54 |
55 |
54.00 |
2.000 |
6 |
‑ |
0 |
1 |
2 |
56 |
58 |
57 |
57 |
57.00 |
0.6667 |
7 |
+ |
0 |
3 |
2 |
49 |
50 |
48 |
51 |
49.50 |
1.6667 |
8 |
0 |
– |
2 |
1 |
40 |
45 |
42 |
45 |
43.00 |
6.000 |
9 |
0 |
+ |
2 |
3 |
56 |
57 |
55 |
58 |
56.50 |
1.667 |
|
|
|
|
|||||||
1.1. Выполним предварительную обработку экспериментальных данных, результаты расчета внесем в таблицу 6.
Выборочное среднее в звездных точках (см. уравнение (6)):
,
![]() .
.
Например, выборочное среднее в опыте № 8:
 .
.
Выборочная дисперсия в звездных точках (см. уравнение (7)):
, .
Например, выборочное среднее в опыте № 8:

Проверка выборочных дисперсий на однородность по критерию Кохрена:
‑ экспериментальное значение критерия Кохрена (см. уравнение (8)):
 ,
,
‑ критическое
значение критерия Кохрена
при числах степеней свободы
,
и доверительной вероятности р
выбирается из таблицы Приложения 5:
![]() .
Вывод:
9 выборочных дисперсий
однородны, так как
.
Вывод:
9 выборочных дисперсий
однородны, так как
![]() .
(см. уравнение (9)).
.
(см. уравнение (9)).
1.2. Так как все выборочные дисперсии однородны, рассчитаем дисперсию воспроизводимости и её число степеней свободы (см. уравнение (11) – (12)):
 ,
,
![]() .
.
2.
Создадим матрицу
моделирования на
базе матрицы ОЦКП
для
построения ортогонализированного
двухфакторного
уравнение
регрессии
второго порядка
![]() (таблица 7). Создадим столбцы N2,
(таблица 7). Создадим столбцы N2,
![]() ,
где ортогонализирующий коэффициент
,
где ортогонализирующий коэффициент
![]() (см. уравнение (32))
и
внесем в матрицу
моделирования
выборочные средние каждого опыта из
таблицы 6.
(см. уравнение (32))
и
внесем в матрицу
моделирования
выборочные средние каждого опыта из
таблицы 6.
Таблица 7. ‑ Матрица моделирования для построения ортогонализированного двухфакторного уравнения регрессии второго порядка на базе ОЦКП.
Nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
‑ |
‑ |
+ |
1/3 |
1/3 |
45.00 |
+45.00 |
‑ 45.00 |
‑ 45.00 |
+45.00 |
1/345.00 |
1/345.00 |
44.59 |
0.1681 |
2 |
+ |
+ |
+ |
– |
1/3 |
1/3 |
36.00 |
+36.00 |
+36.00 |
‑ 36.00 |
‑ 36.00 |
1/336.00 |
1/336.00 |
36.59 |
0.3481 |
3 |
+ |
‑ |
‑ |
– |
1/3 |
1/3 |
57.00 |
+57.00 |
‑ 57.00 |
+57.00 |
‑ 57.00 |
1/357.00 |
1/357.00 |
57.59 |
0.3481 |
4 |
+ |
+ |
+ |
+ |
1/3 |
1/3 |
49.50 |
+49.50 |
+49.50 |
+49.50 |
+49.50 |
1/349.50 |
1/349.50 |
49.59 |
0.0081 |
5 |
+ |
0 |
0 |
0 |
‑ 2/3 |
‑ 2/3 |
54.00 |
+54.00 |
054.00 |
054.00 |
054.00 |
‑ 2/354.00 |
‑ 2/354.00 |
54.99 |
0.9801 |
6 |
+ |
‑ |
0 |
0 |
1/3 |
‑ 2/3 |
57.00 |
+57.00 |
‑ 57.00 |
057.00 |
057.00 |
1/357.00 |
‑ 2/357.00 |
56.79 |
0.0441 |
7 |
+ |
+ |
0 |
0 |
1/3 |
‑ 2/3 |
49.50 |
+49.50 |
+49.50 |
049.50 |
049.50 |
1/349.50 |
‑ 2/349.50 |
48.79 |
0.5041 |
8 |
+ |
0 |
‑ |
0 |
‑ 2/3 |
1/3 |
43.00 |
+43.00 |
043.00 |
‑ 43.00 |
043.00 |
‑ 2/343.00 |
1/343.00 |
42.79 |
0.0441 |
9 |
+ |
0 |
+ |
0 |
‑ 2/3 |
1/3 |
57.50 |
+57.50 |
057.50 |
+57.50 |
057.50 |
‑ 2/357.50 |
1/357.50 |
55.79 |
0.5041 |
|
9 |
6 |
6 |
4 |
2 |
2 |
|
447.5 |
‑ 24.00 |
39.00 |
1.500 |
‑ 4.333 |
‑ 11.33 |
= 2.949 |
|
|
|
49.72 |
‑ 4.000 |
6.500 |
0.3750 |
‑ 2.167 |
‑ 5.665 |
|
|||||||
Уравнение адекватно |
|
0.49 |
0.6 |
0.6 |
0.7 |
1.0 |
1.0 |
||||||||
2.1. Рассчитаем
коэффициенты ортогонализированного
двухфакторного
уравнения регрессии второго
порядка
![]() (значения
(значения
![]() тоже изменятся, так как число опытов
увеличилось с 5-ти до 9-ти).
тоже изменятся, так как число опытов
увеличилось с 5-ти до 9-ти).
Создадим
столбцы
![]() и рассчитаем суммы
и рассчитаем суммы
![]() ,
,
![]() (результаты расчета внести в таблицу
6).
(результаты расчета внести в таблицу
6).
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Рассчитаем суммы
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
 .
.
2.2. Рассчитаем коэффициенты двухфакторного ортогонализированного уравнения регрессии второго порядка (см. уравнения (33) – (36)):
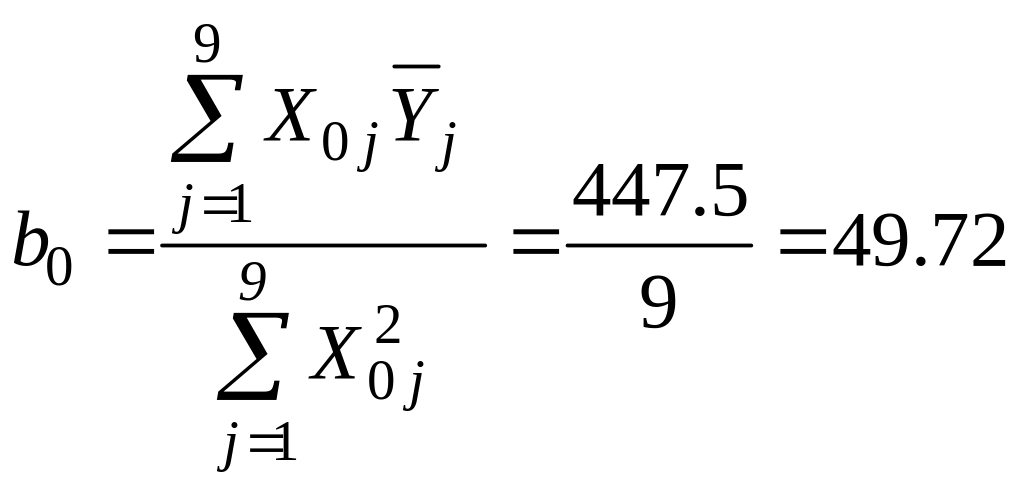 ;
;
 ;
;
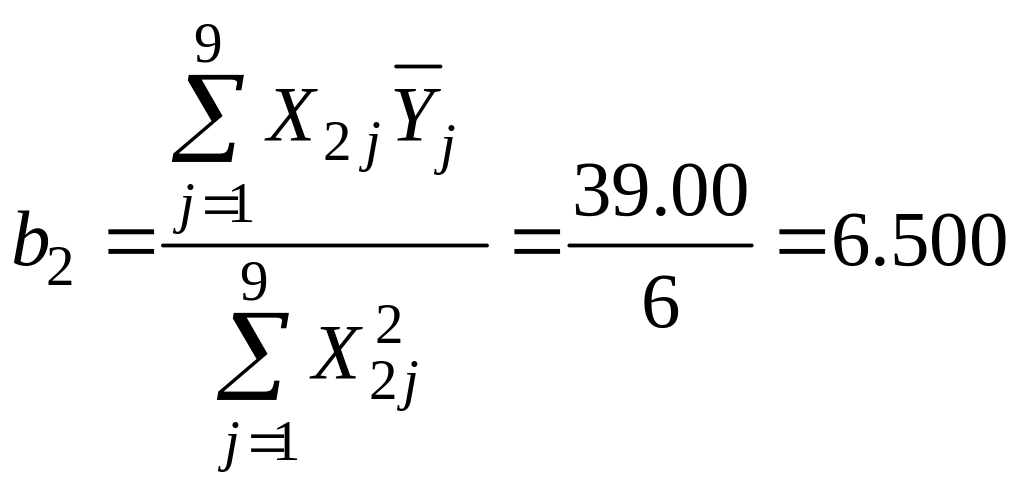 ;
;
 ;
;
 ;
;
 .
.
2.3. Проверим полученные коэффициенты ортогонализированного двухфакторного уравнения регрессии второго порядка на значимость.
Рассчитаем дисперсии значимости коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка (см. уравнения (37) – (43)):
 ;
;
 ;
;
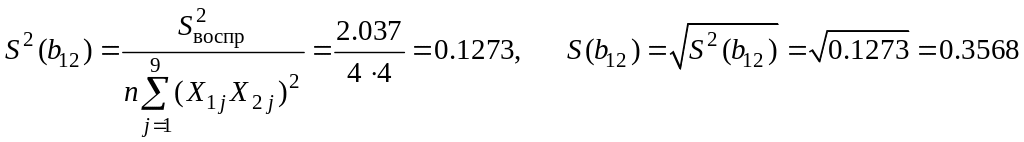 ;
;
 .
.
Рассчитаем
доверительные
интервалы
коэффициентов
ортогонализированного
двухфакторного
уравнения регрессии второго
порядка
![]() по критерию Стьюдента
(см.
уравнения (44) – (50)):
по критерию Стьюдента
(см.
уравнения (44) – (50)):
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
где
![]() – табличное
значение критерия Стьюдента при числе
степеней свободы
– табличное
значение критерия Стьюдента при числе
степеней свободы
![]() и доверительной вероятности р = 0.95
выбираем из таблицы Приложения 2:
и доверительной вероятности р = 0.95
выбираем из таблицы Приложения 2:
Корректно запишем
значения коэффициентов
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Регрессионные
коэффициента
![]() значимы, так как (см. уравнения (51) – (54)):
значимы, так как (см. уравнения (51) – (54)):
![]() ;
;
![]() ,
,
![]() .
.
![]() ,
,
![]()
Регрессионный
коэффициент![]() незначим, так как
незначим, так как
![]() .
.
Вывод:
ортогонализированное
двухфакторное
уравнение регрессии второго
порядка, в котором 5 коэффициентов
![]() значимы,
а коэффициент
незначим, имеет следующий вид:
значимы,
а коэффициент
незначим, имеет следующий вид:
![]() .
.
