35. Інтегрування дробово-раціональних, тригонометричних функцій та ірраціональних функцій.

При обчисленні інтегралів вигляду або від парного степеня синуса або косинуса використовують ф-ли зниження степеня:

При обчислення інтегралів вигляду або від непарного степеня синуса або косинуса треба відокремити від непарного степеня один множник і ввести нову заміну, вважаючи, що cosx=t або sinx=t.

При обчисленні інтегралів вигляду ; ; застосовують ф-ли:

1. 

2. 

3. 

Універсальна тригонометрична підстановка:

Інтеграли від ірраціональних ф-цій є одними із найскладніших.

Основний метод – метод підстановки – заміни змінної.

36. Означення визначеного інтеграла, його основні властивості та геометричний зміст. Формула Ньютона-Лейбніца. Заміна змінної та інтегрування частинами у визначеному інтегралі.

Визначеним інтегралом наз.. границя інтегралів і суми, коли найбільший із проміжків розбиття прямує до нуля.

Основні властивості визначених інтегралів:

1. 

2. Сталий множник виноситься.

3. 

4. 

5. 

6. 

7. 

Геометричний зміст – площа криволінійної границі (фігура обмежена лініями y=f(x) x=a x=b y=0).

Ф-ла Ньютона-Лейбніца:

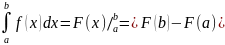
Метод заміни змінної подібний до невизначеного інтегралу. Особливість – слід перерахувати межі.

Інтегрування частинами:

37. Застосування інтегрального числення до обчислення площ плоских фігур. Знаходження довжини дуги плоскої кривої, об'єму тіла обертання.

Знаходження площ плоских фігур:

Об’єми тіл обертання:

Довжина дуги (плоскої кривої):

38. Основні поняття та означення теорії диференціальних рівнянь. Задача Коші.

Диференціальними наз.. р-ння, що містять похідні чи диференціали. Розрізняють за порядком.

Розвязок ДР – ф-ції (геометрично – сімейство інтегральних кривих).

Види розвязків:

1. Загальний – містить С

2. Частинний – при конкретному значенні

3. Особливий.

Задача Коші: Знайти частинний розвязок, що задовільняє початкову умову.

39. Диференціальні рівняння першого порядку: з відокремленими змінними., лінійні та однорідні.

Диференціальними р-ннями першого порядку наз.. р-ння, що містять похідні та диференціали першого порядку.

Р-нням з відокремленими змінними наз.. р-ння виду:

M(x)dx+N(y)dy=0

хdx-ydy=0

Розвязують через загальні інтеграли:

→ →

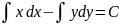
Р-ння з відокремлини змінними:

xdy+ydx=0

ydy+xdx=0

Загальний інтеграл:

xy=e

Точка (0;0) – окремий розвязок.

Лінійним диф.. р-нням першого порядку наз.. р-ння виду:

y’+yf(x)=g(x)

y’+x²y=sinx

Лінійним однорідним р-нням першого порядку нз.. р-ня виду:

y’+y(fx)=0

Розвязують через заміну:

y=uv

40. Диференціальні рівняння другого порядку: рівняння, які допускають пониження порядку; лінійні зі сталими коефіцієнтами.

Лінійні однорідні ДР другого порядку

ay’’+by’+cy=0

Розвязують через характеристичне р-ння:

ak²+bk+c=0

Якщо: 1. K1; k2 – дійсні нерівні (D>0), то y=C₁e^k1x+C₂e^k2x

2. k₁=k₂=k (D=0), то

у=e^kx(C₁x+C₂)

Загальний розвязок: y=C₁e^-3x+C₂e^-1x

41. Числові ряди та їх збіжність; необхідна умова збіжності ряду. Достатні ознаки збіжності для рядів з додатними членами: ознака Даламбера. ознака Коші, ознака порівняння, інтегральна ознака.

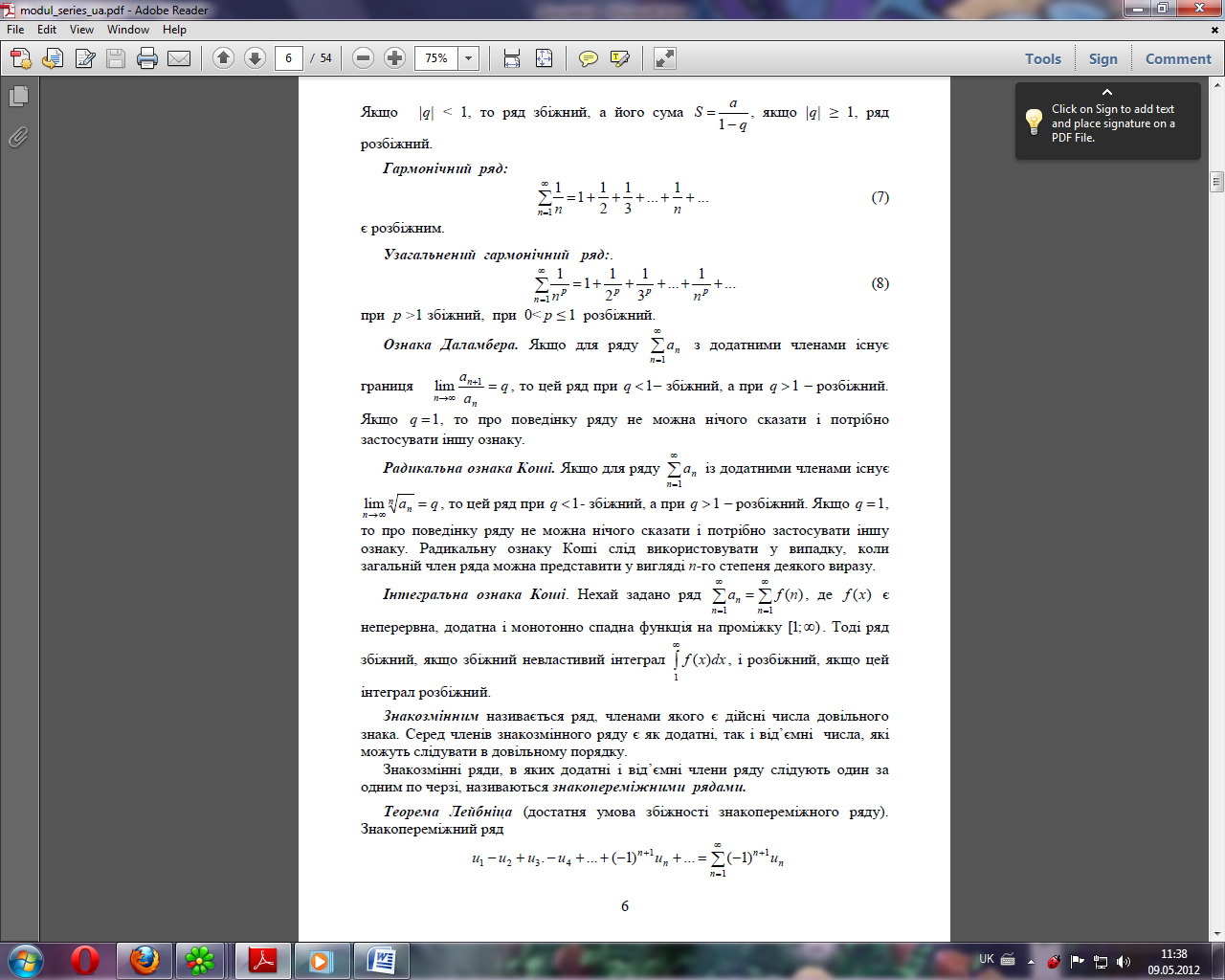
42. Знакозмінні ряди; абсолютна та умовна збіжність знакозмінних рядів. Ознака Лейбніца збіжності.

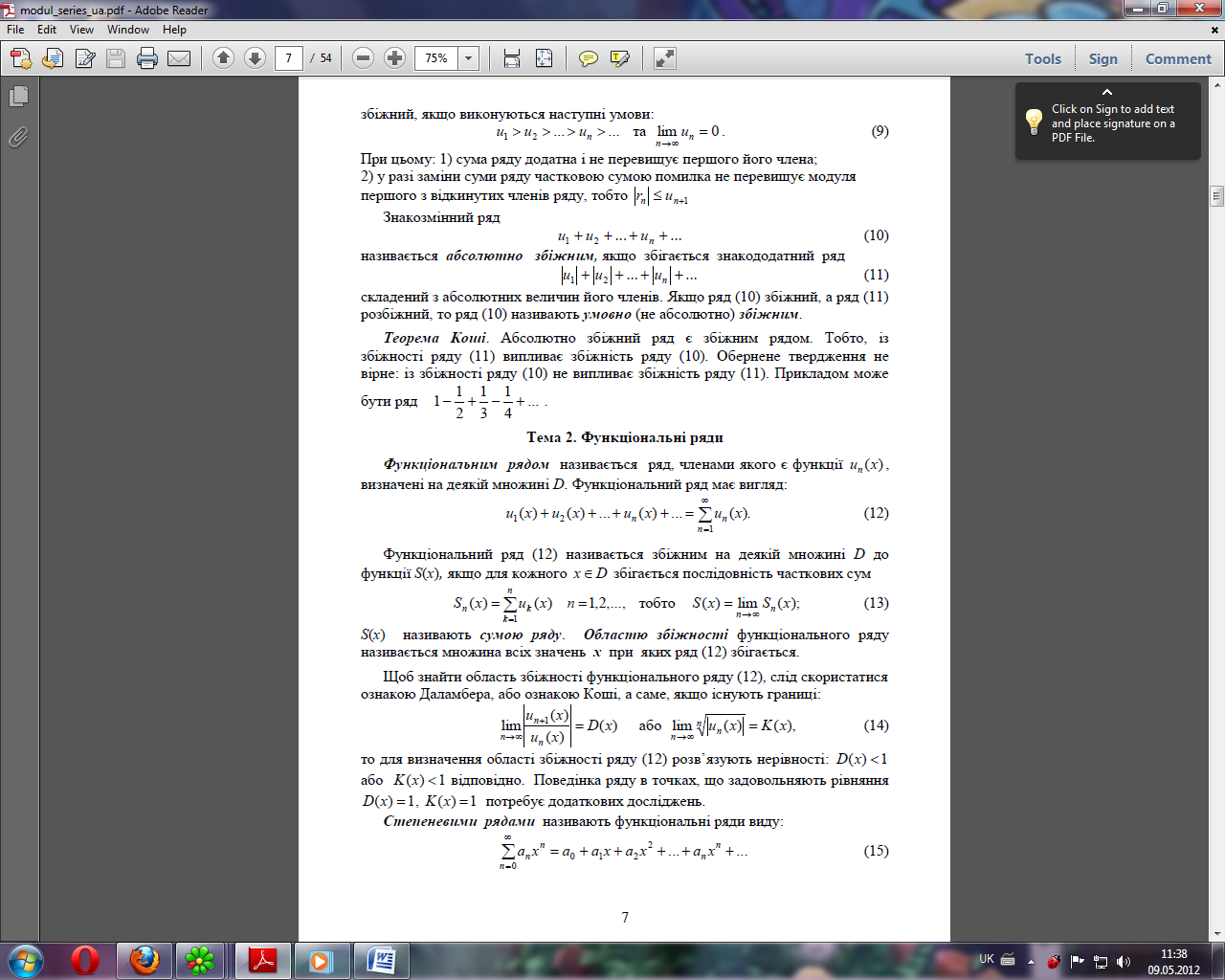
43. Поняття функціонального ряду. Степеневі ряди; інтервал та радіус збіжності степеневого ряду.

44. Розклад функцій в ряди Тейлора та Маклорена.. Застосування рядів для наближених обчислень.