17. Означення функціональної залежності. Функції в економіці. Способи задання функцій.

Ф-ція або ф-на залежність – відповідність між двома множинами, коли кожному елементу з першої множини відповідає не більше як 1 елемент з другої.

Х – незалежна змінна – аргумент.

Y – залежна змінна – ф-ція.

Форми задання: y=f(x) – явна форма. F(x;y)=0 – неявно форма( )

Способи задання ф-цій6 Аналітичний(ф-лами), табличний, словесний.

18. Дослідження основних властивостей функцій: області визначення, парності, непарності. Періодичності за аналітичним заданиям функції.

Основні в-сті ф-ції:

1. Область визначення – це всі можливі значення аргументу х.

Критерії для встановлення області визначення:

• Не можна ділити на 0

• Під логарифмом лише додатні числа

• Під коренем парного степеня лише невід’ємні числа.

2. Множина значень – всі значення, що може набувати залежна змінна у.

3. Ф-ція наз.. парною, якщо для будь-якого х, виконується рівність: f(-x)=f(x). Ф-ція наз.. непарною, якщо f(-x) = - f(x). Якщо ні одна з вище навдених умов не виконується, то ф-ція є ніпарною, ні непарною (загального виду). Парні ф-ції симетричні відносно деякої осі. Непарні ф-ції симетричні відносно точки.

4. Періоди́чна фу́нкція ― функція, яка повтороює свої значення через деякий ненульовий період, тобто не змінює свого значення при додаванні до аргумента фіксованого ненульового числа (періоду).

19. Основні елементарні функції, що зустрічаються в економічних дослідженнях: лінійна, степенева, показникова, логарифмічна (аналітичний вираз, основні властивості, графік).

Функція вважається елементарною, якщо вона може бути побудована з основних елементарних функцій за допомогою скінченного числа алгеб­раїчних дій та суперпозицій.

Основні з них:

1. Лінійна ф-ція – ф-ція виду y=kx+b, де k,b – дійсні числа. Якщо k≠0, то множиною її значень є вся множина, якщо k=0, то множина значень скл.. з одного числа b. Її графік - пряма, не паралельна осі y.

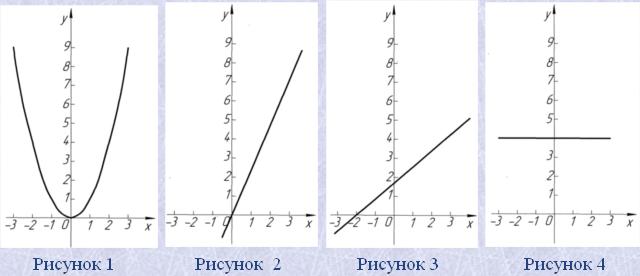
2. степенева у = х^а; Область визначення цієї функції та її графік залежать від значення а.

3. показникова у = а^х, а > 0, а ≠1;

4. логарифмічна у = log_ах, а > 0, а ≠1

20. Поняття числової послідовності. Границя послідовності. Нескінченно малі та нескінченно великі величини, зв'язок між ними.

Числовою послідовністю наз.. відповідність між деякою числовою множиною та множиною натуральних чисел.

Під границею послідовності розуміють число А до якого наближаються члени послідовності, коли їх номери необмежено зростають.

В теорії границь - ∞ - нескінченно велика величина. 0 – нескінченно мала величина. С – стала величина.

∞+∞=∞; С+∞=∞; С*∞=∞; С*0=0; ;

Випадки: ; ; ; ∞-∞; 0*∞ - наз.. невизначеностями.

При знаходженні границь їх розкривають(позбваються). Осноні методи: 1. Розклад на множники. 2. Перетворення із спряженими виразами. 3. Вик.. стандартних границь.

Важливі границі:

- перша визначна границя.

- друга визначна границя. Е = 2,72 – основа натурального логарифма.