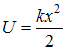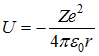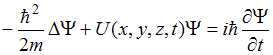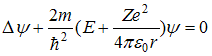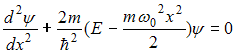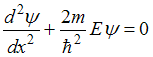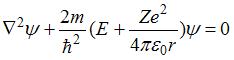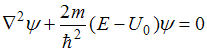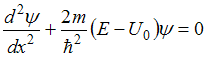Соотношение неопределенностей Гейзенберга
1. Положение пылинки массой
![]() можно
установить с неопределенностью
можно
установить с неопределенностью
![]() Учитывая,
что постоянная Планка
Учитывая,
что постоянная Планка
![]() ,
неопределенность скорости
,
неопределенность скорости ![]() (в
м/с) будет не менее …1,05*10-18
(в
м/с) будет не менее …1,05*10-18
Решение:
Из соотношения неопределенностей
Гейзенберга для координаты и соответствующей
компоненты импульса
![]() следует,
что
следует,
что
![]() .
Здесь
.
Здесь
![]() –
неопределенность координаты,
–
неопределенность координаты,
![]() –
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
![]()
Таким образом,
![]() м/с.
м/с.
2. Неопределенность в определении местоположения частицы, движущейся вдоль оси x, равна длине волны де Бройля для этой частицы. Относительная неопределенность ее скорости не меньше __16___ %.
Решение:
Из соотношения
неопределенностей Гейзенберга для
координаты и соответствующей компоненты
импульса
следует,
что
.
Здесь
–
неопределенность координаты,
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
.
По условию
![]() ,
где
–
длина волны де Бройля, определяемая
соотношением
,
где
–
длина волны де Бройля, определяемая
соотношением
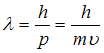 .
Здесь
–
постоянная Планка. Подставляя это
выражение в соотношение неопределенностей,
получаем:
.
Здесь
–
постоянная Планка. Подставляя это
выражение в соотношение неопределенностей,
получаем:
![]()
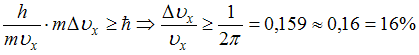
3. Высокая монохроматичность лазерного
излучения обусловлена относительно
большим временем жизни электронов в
метастабильном состоянии, равном
![]() .
Учитывая, что постоянная Планка
.
Учитывая, что постоянная Планка
![]() ,
ширина метастабильного уровня будет
не менее …0,66 пэВ
,
ширина метастабильного уровня будет
не менее …0,66 пэВ
Решение:
Соотношение неопределенностей
для энергии и времени имеет вид
![]() ,
где
,
где
![]() неопределенность
в задании энергии (ширина энергетического
уровня),
неопределенность
в задании энергии (ширина энергетического
уровня),
![]() время
жизни частицы в данном состоянии. Тогда
время
жизни частицы в данном состоянии. Тогда
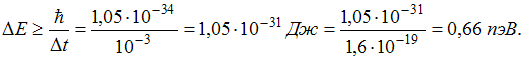
4. Отношение неопределенностей проекций скоростей нейтрона и α-частицы на некоторое направление при условии, что соответствующие координаты частиц определены с одинаковой точностью, равно …4
Решение:
Из соотношения
неопределенностей Гейзенберга для
координаты и соответствующей компоненты
импульса
следует,
что
![]() Здесь
–
неопределенность координаты,
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
.
Неопределенность x-компоненты скорости
можно найти из соотношения
Здесь
–
неопределенность координаты,
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
.
Неопределенность x-компоненты скорости
можно найти из соотношения
![]() Поскольку
соответствующие координаты частиц
определены с одинаковой точностью, то
есть
Поскольку
соответствующие координаты частиц
определены с одинаковой точностью, то
есть
![]() с
учетом того, что
с
учетом того, что
![]() искомое
отношение равно:
искомое
отношение равно:
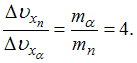
5. Ширина следа электрона на фотографии,
полученной с использованием камеры
Вильсона, составляет
![]() Учитывая,
что постоянная Планка
,
а масса электрона
Учитывая,
что постоянная Планка
,
а масса электрона
![]() неопределенность
в определении скорости электрона будет
не менее 0,12 м/с
неопределенность
в определении скорости электрона будет
не менее 0,12 м/с
Решение:
Из соотношения
неопределенностей Гейзенберга для
координаты и соответствующей компоненты
импульса
следует,
что
,
где
–
неопределенность координаты,
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
.
Неопределенность x-компоненты скорости
электрона можно найти из соотношения
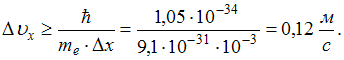
6. Время жизни атома в возбужденном
состоянии 10 нс. Учитывая, что постоянная
Планка
![]() ,
ширина энергетического уровня (в эВ)
составляет не менее …
,
ширина энергетического уровня (в эВ)
составляет не менее …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Соотношение неопределенностей
для энергии и времени имеет вид
,
где
неопределенность
в задании энергии (ширина энергетического
уровня),
время
жизни частицы в данном состоянии. Тогда
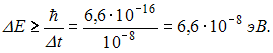
Тема: Уравнения Шредингера (общие
свойства)
1. Стационарное уравнение
Шредингера
![]() описывает
движение свободной частицы, если
потенциальная энергия
имеет
вид …
описывает
движение свободной частицы, если
потенциальная энергия
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Вариант, где
2. Стационарное уравнение Шредингера
имеет вид
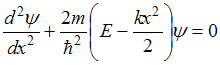 .
Это
уравнение описывает …
.
Это
уравнение описывает …
|
|
|
линейный гармонический осциллятор |
|
|
|
движение свободной частицы |
|
|
|
электрон в трехмерном потенциальном ящике |
|
|
|
электрон в водородоподобном атоме |
Решение: линейный гармонический осциллятор
3. Верным для уравнения Шредингера
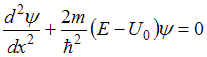 ,
где
,
где
![]() =
const является утверждение:
=
const является утверждение:
|
|
|
Уравнение характеризует движение микрочастицы в области пространства, где потенциальная энергия – постоянная величина. |
|
|
|
Уравнение соответствует трехмерному случаю. |
|
|
|
Уравнение является нестационарным. |
|
|
|
Уравнение описывает линейный гармонический осциллятор. |
Решение:
Уравнение стационарно,
так как волновая функция
![]() не
зависит от времени (отсутствует
производная по времени). Стационарное
уравнение Шредингера в общем случае
имеет вид:
не
зависит от времени (отсутствует
производная по времени). Стационарное
уравнение Шредингера в общем случае
имеет вид:
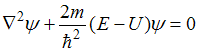 .
Здесь
.
Здесь
![]() потенциальная
энергия микрочастицы. По условию
потенциальная
энергия микрочастицы. По условию
![]() const.
Для гармонического осциллятора
const.
Для гармонического осциллятора
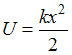 .
Уравнение одномерно. Поэтому из
приведенных утверждений верным является
следующее: «Уравнение характеризует
движение микрочастицы в области
пространства, где потенциальная энергия
– постоянная величина».
.
Уравнение одномерно. Поэтому из
приведенных утверждений верным является
следующее: «Уравнение характеризует
движение микрочастицы в области
пространства, где потенциальная энергия
– постоянная величина».
4. Стационарное уравнение Шредингера
имеет вид
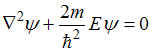 .
Это
уравнение описывает движение …
.
Это
уравнение описывает движение …
|
|
|
частицы в трехмерном бесконечно глубоком потенциальном ящике |
|
|
|
частицы в одномерном бесконечно глубоком потенциальном ящике |
|
|
|
линейного гармонического осциллятора |
|
|
|
электрона в водородоподобном атоме |
Решение:
Бесконечная глубина
ящика (ямы) означает, что потенциальная
энергия частицы внутри ящика равна
нулю, а вне ящика – бесконечности. Таким
образом,
![]() 0.
Поэтому движение частицы в трехмерном
бесконечно глубоком потенциальном
ящике описывает уравнение
0.
Поэтому движение частицы в трехмерном
бесконечно глубоком потенциальном
ящике описывает уравнение
5. Нестационарным уравнением Шредингера является уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
называют
нестационарным (временным) уравнением
Шредингера, так как функция
является
функцией не только пространственных
координат, но и времени, и оно содержит
производную от функции
![]() по
времени.
по
времени.
6. Стационарное уравнение Шредингера
в общем случае имеет вид
.
Здесь
![]() потенциальная
энергия микрочастицы. Одномерное
движение свободной частицы описывает
уравнение …
потенциальная
энергия микрочастицы. Одномерное
движение свободной частицы описывает
уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Свободной называется
частица, не подверженная действию
силовых полей. Это означает, что
![]() .
Кроме того, для одномерного случая
.
Кроме того, для одномерного случая
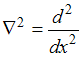 .
Тогда уравнение Шредингера для одномерного
движения свободной частицы имеет вид
.
Тогда уравнение Шредингера для одномерного
движения свободной частицы имеет вид
7. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Трехмерное движение свободной частицы описывает уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Свободной называется частица, не подверженная действию силовых полей. Это означает, что . Поэтому трехмерное движение свободной частицы описывает уравнение .
8. Стационарное уравнение Шредингера описывает электрон в водородоподобном атоме, если потенциальная энергия имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Стационарное уравнение
Шредингера в общем случае имеет вид
![]() Здесь
Здесь
![]() –
потенциальная энергия микрочастицы.
Выражение
представляет
собой потенциальную энергию электрона
в водородоподобном атоме. В этом случае
приведенное уравнение Шредингера
описывает электрон в водородоподобном
атоме.
–
потенциальная энергия микрочастицы.
Выражение
представляет
собой потенциальную энергию электрона
в водородоподобном атоме. В этом случае
приведенное уравнение Шредингера
описывает электрон в водородоподобном
атоме.
9. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Движение частицы в трехмерном бесконечно глубоком потенциальном ящике описывает уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Бесконечная глубина ящика (ямы) означает, что потенциальная энергия частицы внутри ящика равна нулю, а вне ящика – бесконечности. Таким образом, 0. Поэтому движение частицы в трехмерном бесконечно глубоком потенциальном ящике описывает уравнение
10. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Движение частицы вдоль оси ОХ под действием квазиупругой силы описывает уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Для частицы, движущейся вдоль оси ОХ под действием квазиупругой силы, то есть силы, пропорциональной отклонению х частицы от положения равновесия, выражение для потенциальной энергии имеет вид . Кроме того, для одномерного случая . Поэтому движение частицы вдоль оси ОХ под действием квазиупругой силы описывает уравнение .
11. Стационарное уравнение Шредингера
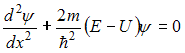 описывает
линейный гармонический осциллятор,
если потенциальная энергия
имеет
вид …
описывает
линейный гармонический осциллятор,
если потенциальная энергия
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Стационарное уравнение
Шредингера в одномерном случае имеет
вид
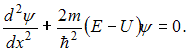 Здесь
Здесь
![]() –
потенциальная энергия. Выражение
представляет
собой потенциальную энергию линейного
гармонического осциллятора. В этом
случае уравнение Шредингера описывает
линейный гармонический осциллятор.
–
потенциальная энергия. Выражение
представляет
собой потенциальную энергию линейного
гармонического осциллятора. В этом
случае уравнение Шредингера описывает
линейный гармонический осциллятор.
12. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Электрону в одномерном потенциальном ящике с бесконечно высокими стенками соответствует уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Для одномерного случая . Кроме того, внутри потенциального ящика U = 0, а вне ящика частица находиться не может, так как его стенки бесконечно высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с бесконечно высокими стенками имеет вид .
Тема: Уравнение Шредингера (конкретные
ситуации)
1. Квантовая и классическая
частицы с энергией Е, движущиеся
слева направо, встречают на своем пути
потенциальный барьер высоты
и
ширины
![]() .
.
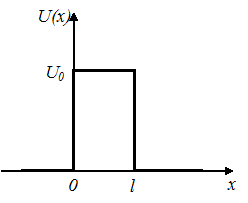 Если
P − вероятность преодоления
барьера, то для …
Если
P − вероятность преодоления
барьера, то для …
|
|
|
квантовой частицы при
|
|
|
|
классической частицы при , а при |
|
|
|
квантовой частицы при
|
|
|
|
квантовой частицы
|
Решение:
Поведение микрочастицы,
встречающей на своем пути потенциальный
барьер, существенно различается с точки
зрения классической и квантовой механики.
По классическим представлениям, если
энергия частицы больше высоты барьера
(
),
частица беспрепятственно проходит над
барьером, то есть вероятность преодоления
барьера
.
Если же
,
то частица отражается от барьера, сквозь
барьер она проникнуть не может и
.
Согласно квантовой механике даже при
имеется
отличная от нуля вероятность отражения
частицы от барьера и, следовательно,
вероятность преодоления барьера
.
При
имеется
отличная от нуля вероятность того, что
частица проникнет сквозь барьер и
окажется в области, где
![]() ,
то есть
.
,
то есть
.
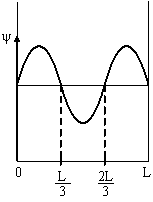
2. Электрон находится в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками в состоянии
с квантовым числом n = 3. Если
![]() -функция
электрона в этом состоянии имеет вид,
указанный на рисунке,
-функция
электрона в этом состоянии имеет вид,
указанный на рисунке,
 то
вероятность обнаружить электрон в
интервале от
то
вероятность обнаружить электрон в
интервале от
![]() до
до
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
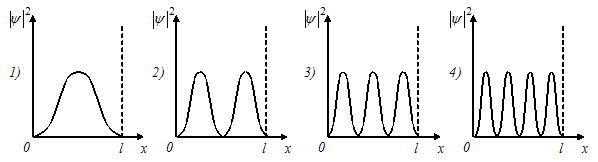
3й график относится к состоянию
с квантовым числом n = 3. Так как
площадь под кривой равна 1, а интервалу
от
до
соответствует
ровно
![]() площади, то вероятность обнаружить
электрон равна
площади, то вероятность обнаружить
электрон равна
![]()
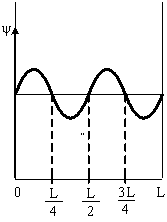
3. Электрон находится в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками в состоянии
с квантовым числом n = 4. Если
-функция
электрона в этом состоянии имеет вид,
указанный на рисунке, то вероятность
обнаружить электрон в интервале от
![]() до
до
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вероятность обнаружить
микрочастицу в интервале (a, b) для
состояния, характеризуемого определенной
-функцией,
равна
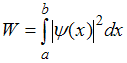 .
Из графика зависимости
.
Из графика зависимости
![]() от
х эта вероятность находится как
отношение площади под кривой
в
интервале (a, b) к площади под кривой
во всем интервале существования
от
х эта вероятность находится как
отношение площади под кривой
в
интервале (a, b) к площади под кривой
во всем интервале существования
![]() ,
то есть в интервале (0, L). Очевидно,
что график зависимости
от
х схематически можно представить
следующим образом:
,
то есть в интервале (0, L). Очевидно,
что график зависимости
от
х схематически можно представить
следующим образом:
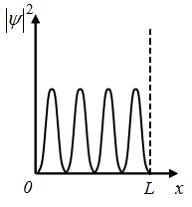 Тогда
вероятность обнаружить электрон в
интервале от
до
равна
.
Тогда
вероятность обнаружить электрон в
интервале от
до
равна
.
4. На рисунках схематически представлены
графики распределения плотности
вероятности по ширине одномерного
потенциального ящика с бесконечно
высокими стенками для состояний электрона
с различными значениями главного
квантового числа n:
В
состоянии с n = 2 вероятность обнаружить
электрон в интервале от
![]() до
до
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Вероятность обнаружить микрочастицу в интервале (a, b) для состояния, характеризуемого определенной -функцией, равна . Из графика зависимости от х эта вероятность находится как отношение площади под кривой в интервале (a, b) к площади под кривой во всем интервале существования , то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости : n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с n = 2 вероятность обнаружить электрон в интервале от до равна .
5. На рисунках схематически представлены
графики распределения плотности
вероятности обнаружения электрона по
ширине одномерного потенциального
ящика с бесконечно высокими стенками
для состояний с различными значениями
главного квантового числа n.
В
состоянии с n = 4 вероятность обнаружить
электрон в интервале от
![]() до
равна …
до
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Вероятность обнаружить микрочастицу в интервале (a, b) для состояния, характеризуемого определенной -функцией, равна . Из графика зависимости от х эта вероятность находится как отношение площади под кривой в интервале (a, b) к площади под кривой во всем интервале существования , то есть в интервале (0, l). При этом состояниям с различными значениями главного квантового числа n соответствуют разные кривые зависимости : n = 1 соответствует график под номером 1, n = 2 – график под номером 2 и т.д. Тогда в состоянии с n = 4 вероятность обнаружить электрон в интервале от до равна .
6. В результате туннельного эффекта вероятность прохождения частицей потенциального барьера увеличивается с …
|
|
|
уменьшением массы частицы |
|
|
|
увеличением ширины барьера |
|
|
|
уменьшением энергии частицы |
|
|
|
увеличением высоты барьера |
Решение:
Вероятность прохождения частицей
потенциального барьера или коэффициент
прозрачности определяется формулой:
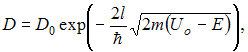 где
где
![]() постоянный
коэффициент, близкий к единице,
постоянный
коэффициент, близкий к единице,
![]() ширина
барьера,
ширина
барьера,
![]() масса
частицы,
масса
частицы,
![]() высота
барьера,
высота
барьера,
![]() энергия
частицы. Следовательно, вероятность
прохождения увеличивается с уменьшением
массы частицы.
энергия
частицы. Следовательно, вероятность
прохождения увеличивается с уменьшением
массы частицы.
7. В результате туннельного эффекта вероятность прохождения частицей потенциального барьера уменьшается с …
|
|
|
увеличением ширины барьера |
|
|
|
уменьшением массы частицы |
|
|
|
увеличением энергии частицы |
|
|
|
уменьшением высоты барьера |
Решение: Вероятность прохождения частицей потенциального барьера или коэффициент прозрачности определяется формулой: где постоянный коэффициент, близкий к единице, ширина барьера, масса частицы, высота барьера, энергия частицы. Следовательно, вероятность прохождения уменьшается с увеличением ширины барьера.