Вопросы к первому блоку, 2011-2012 уч. Год, утс-11, уэл-11, уба-11,12

1. Опр. ДУ, ОДУ. Пр. 2. Опр. ОДУ -го порядка, разрешенного (не разрешенного) относи тельно производной. 3. Опр. решения ОДУ и интегральной кривой. Пр. 4. Опр. задачи Коши, условий и данных Коши. 5. Опр. общего, частного и особого решений. 6. Что значит проинтегрировать в явном виде и в квадратурах? Пр. 7. Опр. НСОДУ, его порядка и задачи Коши. 8. Опр. НСЛДУ, однородной НСЛДУ и линейно независимых решений.

9. Опр. фундаментальной системы решений, фундамент. матрицы и вронскиана. 10. Опр. переходной матрицы и ее свойства. 11. Опр. ЛДУ -го порядка и его свойства. 12. Опр. сетки и сеточной функции. 13. Опр. локальной, глобальной погрешностей и метод Эйлера. 14. Опр. функционального преобразователя и булевой функции. 15. Опр. логической формулы, штриха Шеффера и закона поглощения. 16. Опр. конъюнкта и СДНФ. 17. Опр. замыкания, функционально полного множества булевых функций. 18. Опр. базиса булевых функций и теорема Шеннона. 19. Опр. импликанты, простой и существенной (ядровой) импликант. 20. Опр. тупковой ДНФ и минимальной ДНФ.

Вопросы ко второму блоку, 2011-2012 уч.Год

1. Опр. шара, ограниченного и открытого множества в . 2. Опр. отображения, функции n переменных и координатных функций. 3. Опр. С-линии и С-поверхности уровня. Пр.

4. Опр. и свойства предела отображений и функций. 5. Опр. дифференцируемого отобра жения, производной и дифференциала отображения в точке. 6. Опр. матриц Якоби отображения и матрицы Гессе функции. Пр. , . 7. Опр. частной производной, произв. по направлению и формула вычисления. 8. Опр. градиента и его свойства. 9. Геом. смысл дифференцируемости и уравнение касательной поверхно сти. 10. Опр. смешанной производной, производной второго порядка и замечания.

11. Опр. многочлена Тейлора и аппроксимации функции. 12. Формулировка необходимых и достаточных условий локального экстремума. 13. Опр. функций Дирихле, гребешка и щетки Дирихле. Св. 14. Опр. цилиндрического тела и геометрический смысл двойного интеграла.

15. Опр. двойного интеграла и его свойства. 16. Геометрический смысл двойного интеграла. Приложения. 17. Опр. интеграла с переменным верхним пределом и повторного интеграла. 18. Опр. КИВР. Формула вычисления и приложение. 19. Опр., формула вычисления и приложение тройного интеграла. 20. Опр. двусторонней поверхности. КПР. Понятие ориентации. 21. Опр. ПИВР. Формула вычисления и приложения. 22. Опр. дивергенции и формула Гаусса-Остроградского. Пр. и физический смысл. 23. Опр. ротора векторного поля и формула Стокса. Пр. и физический смысл. 24. Опр. соленоидального, потенциального и гармонического полей. Т. Гельмгольца.

Типы задач для экзамена

1. Найти общий интеграл . 2. Решить задачу Коши . 3. Решить задачу Коши 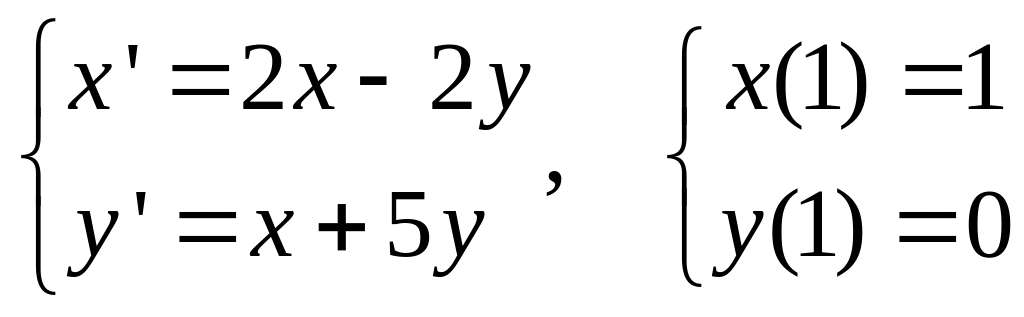4. Минимизировать логическую формулу . 5. Найти линию уровня функции . 6. Вычислить в точке . 7. Найти точки экстрему ма функции на множестве. 8. Нарисовать область и изменить порядок интегрирования в повторном интеграле . 9. Вычислить двойной интеграл . 10. Вычислить площадь фигуры, ограниченной кривыми . 11. Найти работу силового поля вдоль кривой . 12. Найти абсолютную и относительную погрешности произведения и частного двух приближенных величин.