Глава 4

ОТОБРАЖЕНИЯ И ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Определение Лучом в с естественным базисом, выходящим из точки , с направляющим вектором называется множество .

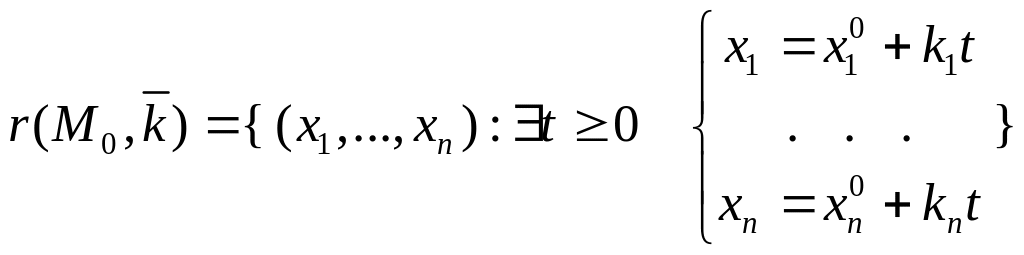Определение Шаром с центром в точке и радиусом ( -окрестностью точки ) называется множество

.

Определение Множество называется открытым, если каждая точка входит в него вместе с некоторой своей окрестностью .

Определение Множество называется замкнутым, если его дополнение является открытым множеством.Множество - называется замкнутым шаром и является замкнутым множеством.

Определение Множество в называется ограниченным, если оно содержится в некотором шаре .

Определение Пусть множество . Отображение , ставящее в соответствие каждой точке точку , называется отображением от переменных .

Определение Отображение называется функцией от переменны.

Квадратичная форма является функцией от переменных, точнее однородным многочленом второго порядка от переменных.

Булева функция это функция с тремя двоичными переменными , областью определения и областью значений .

Определение Отображение определяет и вполне определяется функциями от переменных по правилу

.

Функции называются координатными.

О пределение Пусть . - линией уровня функ ции называется множество точек .

Определение Пусть . - поверхностью уровня функции называется множество точек

.

____

Определение Пусть - предельная точка множества и отображение . Точка называется пределом

отображения при , если

.

ЗАМЕЧАНИЕ Определения предельной точки и предела являются прямым обобщением соответствующих определений в одномерном случае.

Обозначение . Если определены в окрестности точки , то индекс в обозначениях опускают.

Определение Пусть отображение определено в окрестности точки и задан луч . Говорят, что имеет предел в точке по направлению , если существует конечный предел

.

ТЕОРЕМА 4.1 (свойства пределов)

1) . 2) Если , - предельная точка и существует , то .

3) Если предел в точке M существует, то он единственен.

4) .

5) .

6) 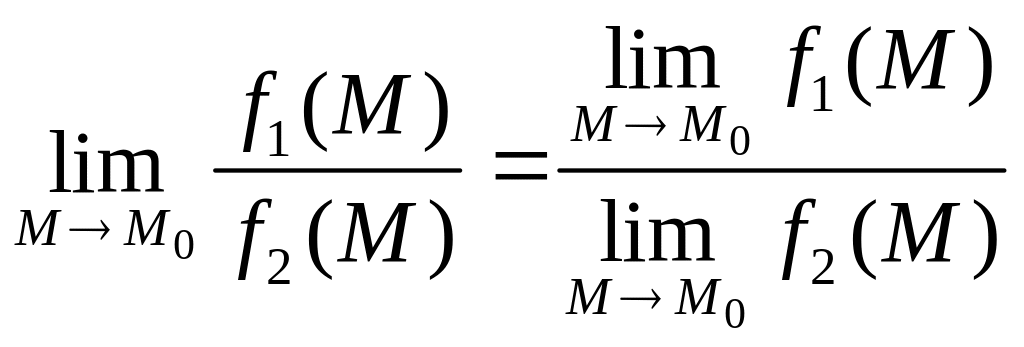, если предел знаменателя не равен 0.

_____

Определение Пусть и является его предельной точкой. Отображение называется непрерывным в точке , если существует предел .

Определение Отображение называется непрерывным на множестве, если оно непрерывно в каждой точке множества.

Определение Пусть даны переменная точка и фикси рованная точка . Полным приращением переменной в точке называется вектор , а полным приращением отображения в точке называется вектор .

Определение Для точки только с -ой переменной координатой соответствующий вектор называется частичным приращением отображения в точке по переменной .

ТЕОРЕМА 4.2 (свойства непрерывных отображений)

1) Отображение непрерывно в точке тогда и только

тогда, когда его координатные функции , непрерывны

в этой точке.

2) Отображение непрерывно в точке тогда и только тогда, когда

.

3) Если непрерывно в точке , то оно непрерывно в этой точке

по каждой переменной, Обратное утверждение, вообще говоря,

неверно.

4) Если функции непрерывны в точке , то их линейная

комбинация , произведение и частное непрерывны

в этой точке, в последнем случае при условии .

5) Пусть отображение непрерывно в точке и

. Если отображение непрерывно в точке

, тогда композиция отображений непрерывна в

точке .

6) Непрерывная на замкнутом ограниченном множестве функция

достигает на этом множестве своих наибольшего и наименьшего

значений.

_____

Определение Пусть отображение определено в окрестно сти точки . Оно называется дифференцируемым в точке , если полное приращение в этой точке представимо в виде , где - линейный оператор, определяемый отображением и точкой , , а отображение определено на окрестности точки и обладает свойством .

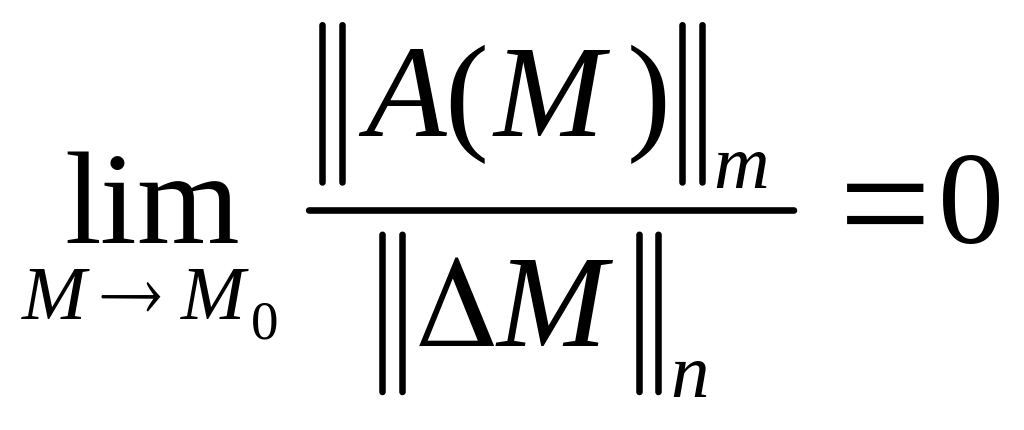ЗАМЕЧАНИЕ Полное приращение отображения в координатной форме имеет вид ,

где . Матрица имеет размер и называется матрицей Якоби отображения в точке .

Замечание позволяет дать такое

Определение Пусть функция определено в окрестности точки . Она называется дифференцируемой в точке , если ее полное приращение в этой точке представимо в виде

,

где - некоторые числа, а функция обладает свойством

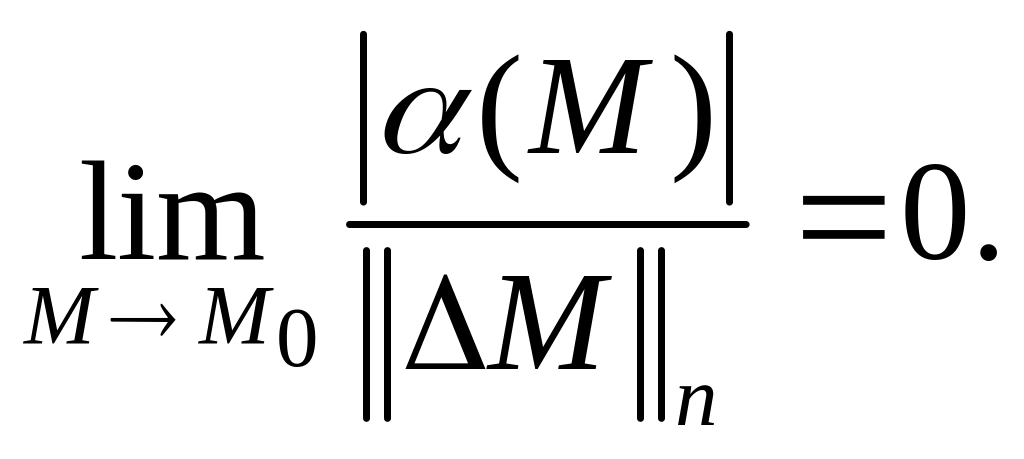
Определение Если отображение дифференцируемо в точке , то слагаемое называется дифференциалом (главной частью приращения ) отображения в точке . Линейный оператор называется производной отображения в точке .

ЗАМЕЧАНИЕ В частном случае функции

есть дифференциал функции в точке .

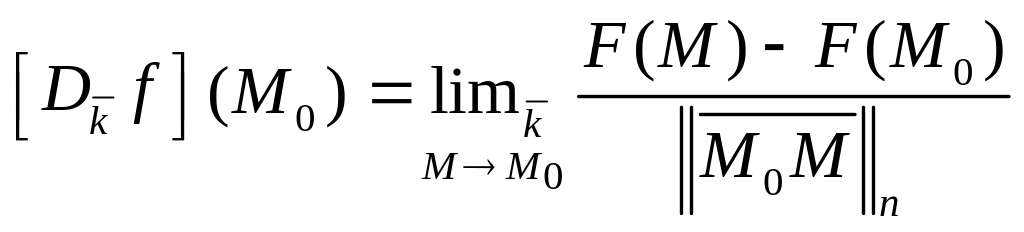Определение Пусть функция определена в окрестности точки , и - единичный вектор в , задан ный своими направляющими косинусами ( . Производной функции в точке по направлению называется конечный предел , если он существует.

Определение Пусть функция определена в окрестности точки . Частной производной функции в точке по переменной называется конечный предел , если он существует.

Определение Если функция имеет частные производные по

всем переменным в точке , то ее градиентом в точке называ

ется вектор .

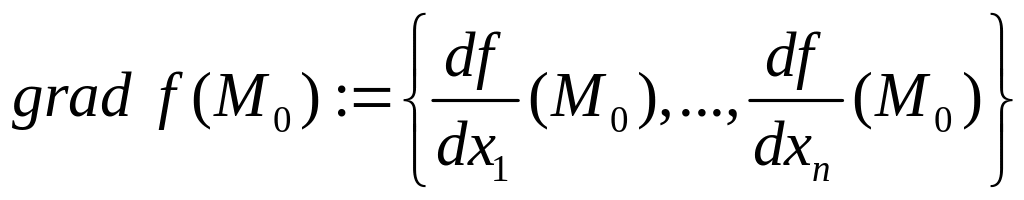ТЕОРЕМА 4.3 (свойства дифференцируемого отображения)

1) Отображение дифференцируемо в точке тогда и только

тогда, когда координатные функции дифференциру

емы в этой точке.

2) Если дифференцируемо в точке , то матрица Якоби

в этой точке имеет вид

.

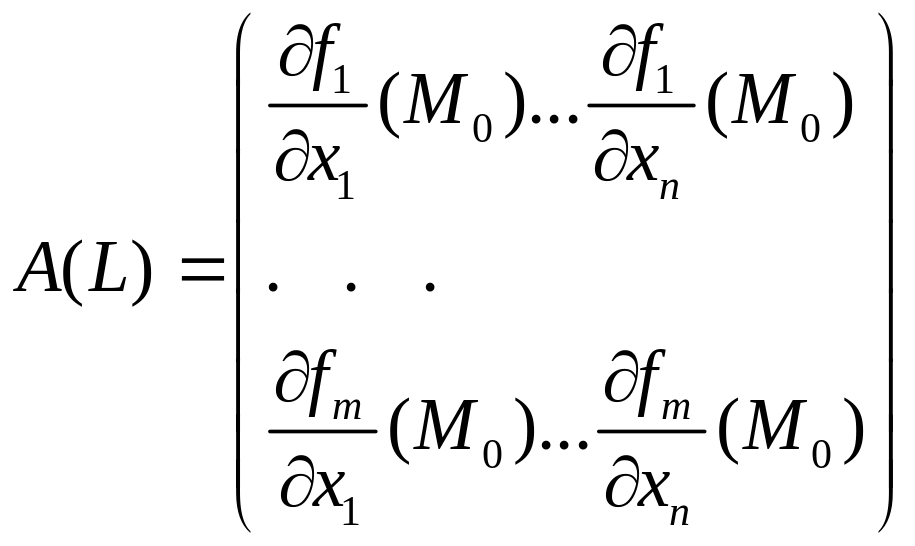В частности, если дифференцируема в точке , то дифферен

циал функции .

3) Если функция дифференцируема в точке , то она

дифференцируема в этой точке по каждому направлению

, и производная

.

4) Градиент функции определяет направление , произ

водная по которому будет максимальной : .

При этом в противоположном направлении производная будет

минимальной.

ЗАМЕЧАНИЕ Рассмотрим кривую в области определения

функции, в каждой точке которой касательная имеет направле

ние . Множество соответствующих точек

графика функции называется линией наискорейшего спуска. Это

объясняется тем, что для каждой точки кривой величина

спуска точки по поверхности будет

наибольшей при движении по этой кривой.

_____

Определение Пусть функция определена в окрестности точки . Плоскость называется касательной плоскостью к графику функции в точке

, если для переменной точки

(Рис.4. ).

В этом случае говорят коротко, что функция имеет

касательную плоскость в точке .

Определение Если функция имеет касательную плоскость в точке , то прямая, проходящая через точку и перпендикулярная к этой касательной плоскости, называется нормалью к поверхности.

ЗАМЕЧАНИЕ (геометрический смысл дифференциала)

График функции имеет невертикальную ( ) касательную

плоскость в точке тогда и только тогда, когда

функция дифференцируема в точке . В этом случае

уравнение касательной плоскости имеет вид

,

а уравнение нормали к поверхности - вид

.

_____

Определение Пусть функция имеет частную производную в каждой точке некоторой окрестности. Если существует частная производная функции в точке по переменной , то в случае она обозначается и называется смешанной производной, а в случае она обозначается и называется частной производной второго порядка по переменной .

Можно доказать такое

ЗАМЕЧАНИЕ Если существуют смешанные производные

в окрестности точки и хотя бы одна из

них непрерывна в этой точке, то они совпадают. В дальнейшем

молчаливо предполагается совпадение этих производных.

ТЕОРЕМА 4.4 (о сложном отображении)

Пусть есть открытое множество в , - открытое множество в

. Пусть отображение - дифференцируемо в точке

, отображение дифференцируемо в точке

. Тогда отображение дифференцируемо в

точке и его матрица Якоби совпадает с произведением матриц

Якоби отображений в и в соответствующих точках:

.

Доказательство является обобщением соответствующего доказательства для случая функции одной переменной, и на нем мы останавливаться не будем.

Равенство называется формула полной производной. Формулы вычисления частных производных сложной функции .

_____

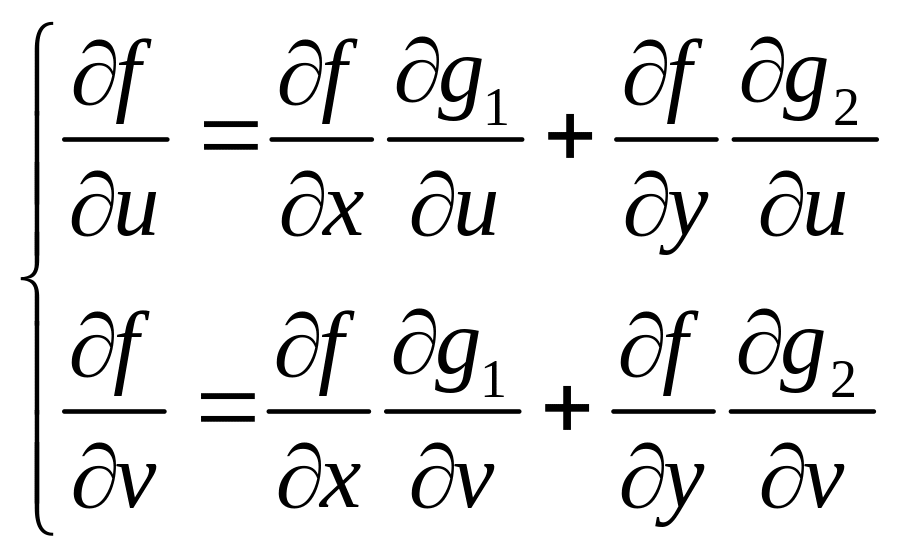ТЕОРЕМА 4.5 (формула Тейлора функции двух переменных)

Пусть функция имеет непрерывные частные производ

ные до -го порядка включительно в окрестности точки

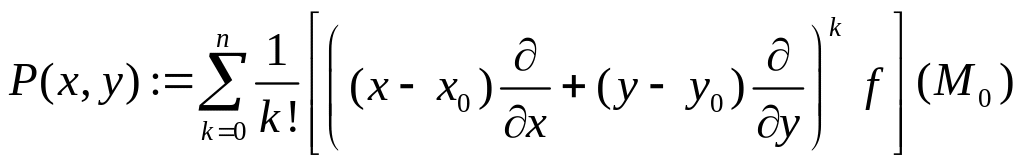; - многочлен

Тейлора функции в окрестности точки , записанный в

символической форме. Тогда в окрестности этой точки имеет место

формула Тейлора с остаточным членом в

форме Лагранжа

,

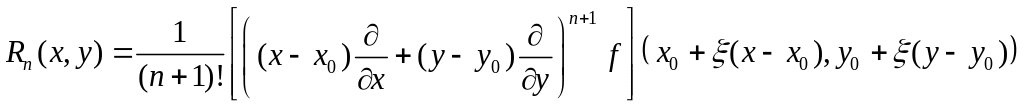где .

Определение Аппроксимировать функцию на множест ве многочленом с заданной точностью - это значит найти многочлен со свойством : .

ЗАМЕЧАНИЕ Аналогичная формула Тейлора имеет место и для

функции от переменных.

_____

Для формулировки необходимых и достаточных условий локального экстремума функции нескольких переменных нам понадобится классификация квадратичных форм и некоторые ее свойства.

Определение Квадратичная форма называется положительно (отрицательно) определенной, если

.

Определение Квадратичная форма называется полу-

определенной, если или , причем .

Определение Квадратичная форма называется неопределенной, если .

Определение Миноры матрица квадратичной формы

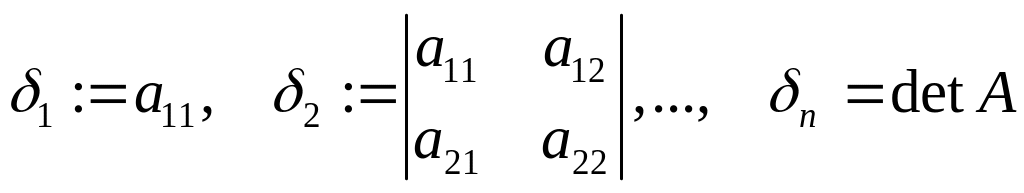
называются главными минорами.

ЗАМЕЧАНИЕ 1 Пусть квадратичная форма

симметричная. 1) Равносильны утверждения:

а) положительно определена;

б) (критерий Сильвестра) Все главные миноры ее матрицы

положительны;

в) все собственные числа ее матрицы положительны.

2) отрицательно определена тогда и только тогда, когда

последовательность главных миноров ее матрицы коэффициентов

знакочередующаяся:

.

3) неопределенная тогда и только тогда, когда собственные

числа ее матрицы имеют разные знаки.

Определение Матрицей Гессе функции , имеющей частные производные второго порядка, называется матрица

.

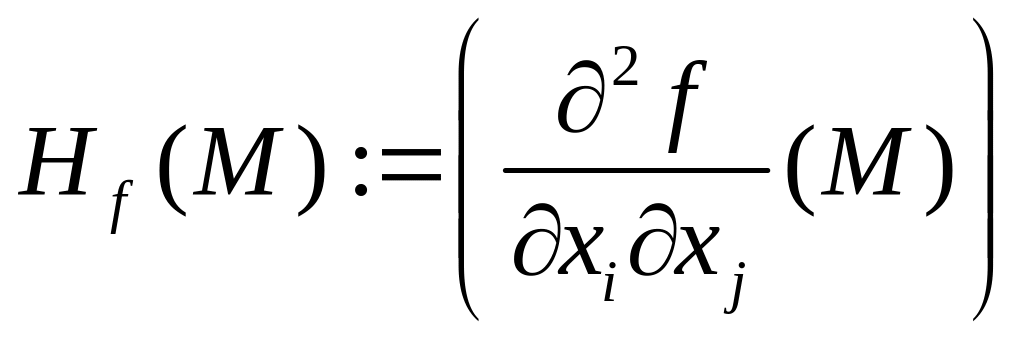Определение точки локального экстремума естественным образом обобщается на функции нескольких переменных.

Определение Пусть функция определена на мно жестве , точка и является предельной точкой. Говорят, что является точкой локального максимума (минимума), если

.

При этом называется локальным максимумом (минимумом).

ТЕОРЕМА 4.6 (необходимое и достаточное условие локального

экстремума)

1) Если функция имеет локальный экстремум в точке

и имеет частные производные в этой точке, то

.

2) Пусть имеет непрерывные частные производные до второго

порядка включительно в точке и . Тогда:

а) если квадратичная форма

положительно определенная, то есть точка локального

минимума;

б) если отрицательно определенная, то есть точка

локального максимума;

в) если является неопределенной, то - седловая точка:

г) если полуопределенная, то нужны дополнительные

исследования.