Численное решение задачи Коши для оду

Опр Сеткой с шагом и узлами называется разбиение отрезка точками . Сеточной функцией называется функция, определенная в узлах .

Пусть правая часть ОДУ имеет непрерывные частные производные в точке . Тогда по формуле Тейлора в окрестности точки для решения задача Коши: , имеем

.

Последнее равенство подводит к такому определению.

Опр Методом Эйлера приближенного решения задачи Коши на сетке называется нахождение сеточной функции по формулам

.

ЗАМЕЧАНИЕ Локальная погрешность метода Эйлера – это погрешность на одном шаге, и она равна, как следует из формулы Тейлора, . Глобальная погрешность – это величина . Для метода Эйлера она равна .

Опр Методом Рунге-Кутта приближенного решения задачи Коши на сетке называется нахождение сеточной функции по формулам

, где , .

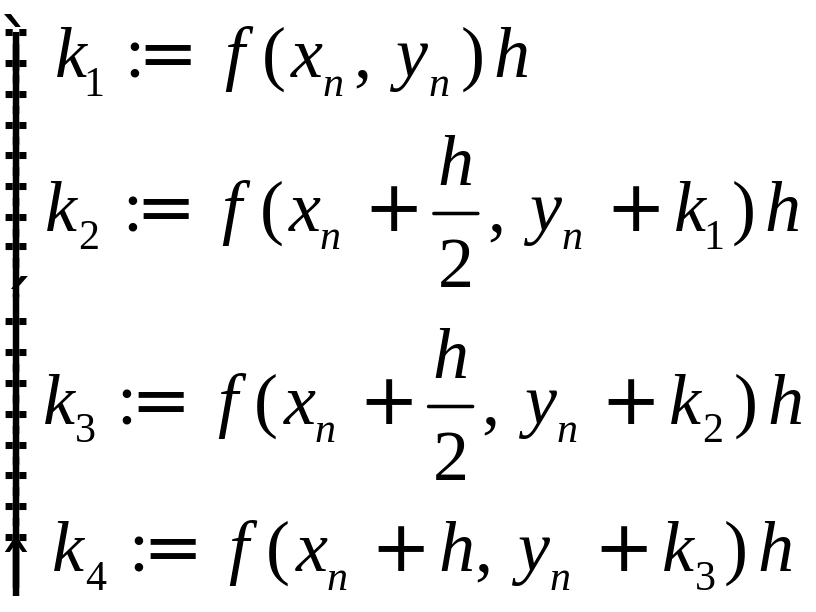ЗАМЕЧАНИЕ 1 Локальная погрешность метода Рунге-Кутта на одном шаге равна . Глобальная погрешность равна .

КПР Задачу Коши можно решить приближенно методом Рунге-Кутта на любом отрезке . Однако точное решение единственно и имеет вид . Это видимое противоречие объясняется тем, что при определении глобальной оценки предполагается существование решения на всем отрезке, что в данном случае имеет место только на . Известны результаты, позволяющие определить характер точного решения по поведению приближенного.

ЗАМЕЧАНИЕ 2 Методы Эйлера и Рунге-Кутта имеют место и для НСОДУ.

Пример Для задачи Коши 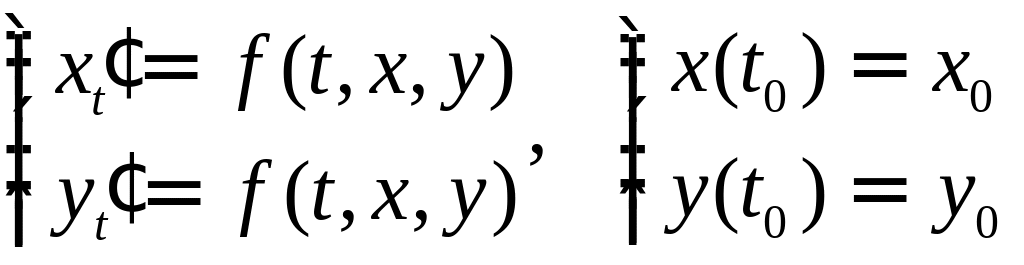формула метода Рунге-Кутта имеет вид 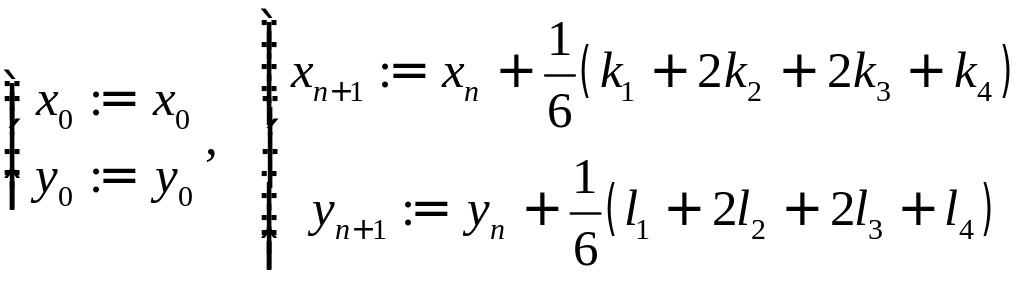, где

.

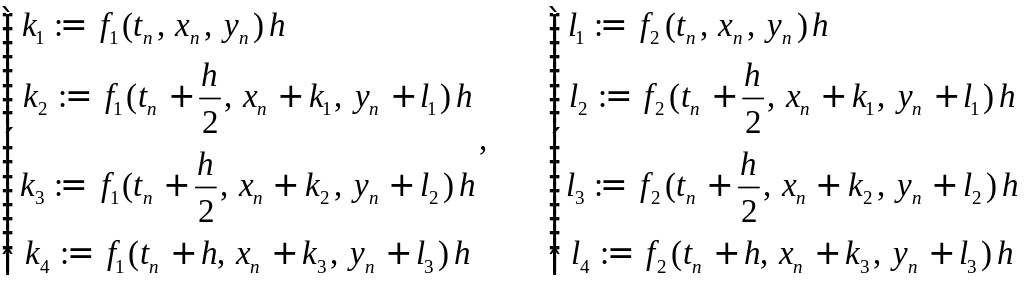Функциональные преобразователи и схемы

Опр Обозначим множество . Отображение называется функциональным преобразователем. Отображение называется двоичной (булевой) функцией от двоичных переменных.

ЗАМЕЧАНИЕ 1 Функциональный преобразователь является отображе нием , координатные функции которого есть булевы функции от переменных.

ЗАМЕЧАНИЕ 2 Существуют постоянные булевы функции и . Булевы функции, не содержащие переменных называются нульарными.

ЗАМЕЧАНИЕ 3 Существует булевых функции относительно одной двоичной переменной (унарные). Их табличное задание следующее:

– тождественная, , - постоянные, - отрицание.

ЗАМЕЧАНИЕ 4 Существует булевых функций от двух двоичных переменных (бинарные операции):

											...
											.
											…
											…
											…

- дизъюнкция; - конъюнкция; - имплика ция; - сложение по модулю два; - эквиваленция; - штрих Шеффера; - стрелка Пирса.

ЗАМЕЧАНИЕ 5 Существует булевых функций от двоичных переменных.

Опр Булева функция задаваемая в виде упорядоченной системы унарных и бинарных операций над входящими в неё двоичными переменными и постоянными , , называется логической формулой (переключательной функцией).

ЗАМЕЧАНИЕ Приоритет выполнения операций в логической формуле задаётся с помощью скобок, а также в следующей последовательности: 1) отрицание; 2) конъюн кция; 3) дизъюнкция; 4) все остальные бинарные операции, при этом оследовательно-

сть их выполнения также должна регулироваться скобками.

Пример Логическая формула имеет такое табличное задание

ЗАМЕЧАНИЕ Булевы функции могут задаваться аналитически, графически, таблич но, в векторной форме и в виде логических схем.

Опр Логическая формула называется тавтологией(тождественно-ложной), если порождаемая ею булева функция тождественно равна единице (нулю).