Нормальная система обыкновенных дифференциальных уравнений

Опр Нормальной системой обыкновенных дифференциальных уравнений (НСОДУ) называется система вида 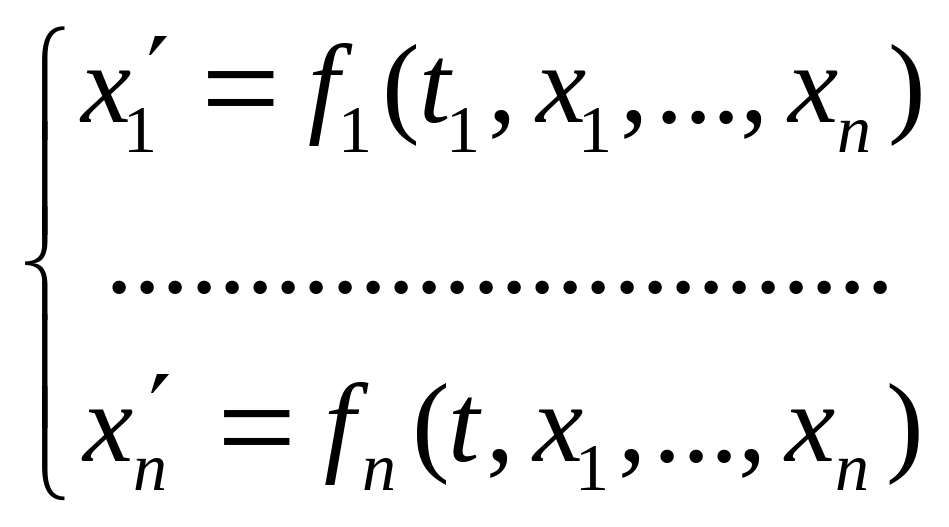, где функции непрерыв ны на открытом множестве , а последовательность неизвестных функций называется решением системы. Число называется порядком НСОДУ.

Опр Если - решение НСОДУ в окрестности точки , то кривая в называется интегральной кривой.

Опр Пусть . Задачей Коши для НСОДУ с начальными условиями

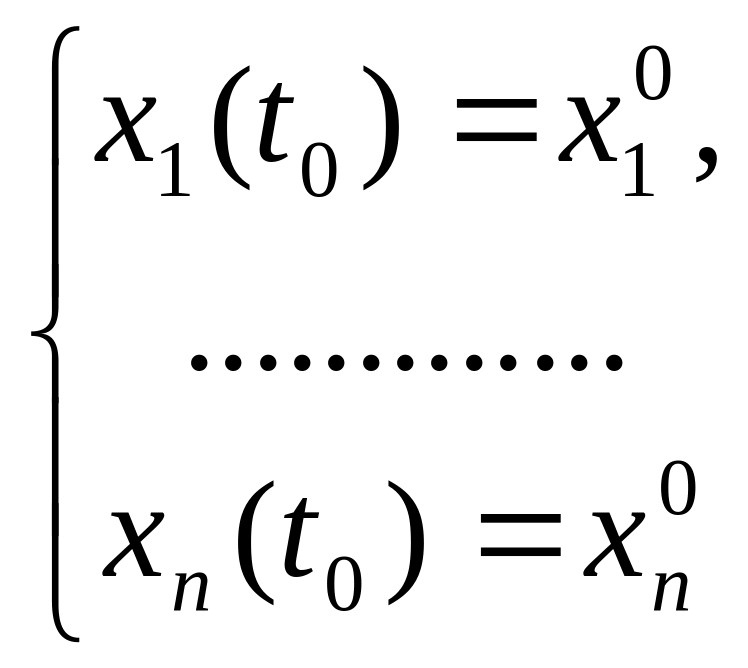называется задача нахождения решения системы в окрестности точки ,

которое удовлетворяет этим условиям.

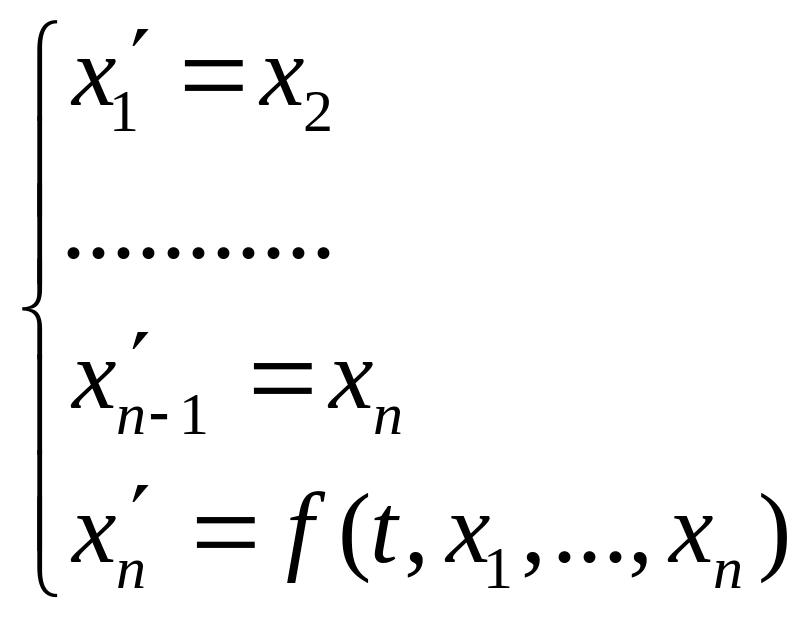Пример Решение задачи Коши для ОДУ го порядка с начальны ми условиями равносильно нахождению решения задачи Коши для НСОДУ с начальными условиями .

◄ В ОДУ го порядка введем новые переменные

Кроме того, дифференцируя эти равенства, получим требуемую систему. ►

Опр Функция удовлетворяет условию Липшица по переменным на множестве , если

ЗАМЕЧАНИЕ Если функция дифференцируема в каждой точке области , то она удовлетворяет условию Липшица на любом ограниченном замкнутом множестве (компакте) из . Если удовлетворяет условию Липшица, то она непрерывна по совокупности переменных в каждой точке из .

ТЕОРЕМА 1 Пусть функции непрерывны на открытом множестве и удовлетворяют условию Липшица по на любом компакте в . Тогда в окрестности точки существует единственное решение задачи Коши для НСОДУ с начальным условием . Если отказаться от условия Липшица, то решение задачи Коши существует, но оно, вообще говоря, неединственное. (Без доказательства)

_____

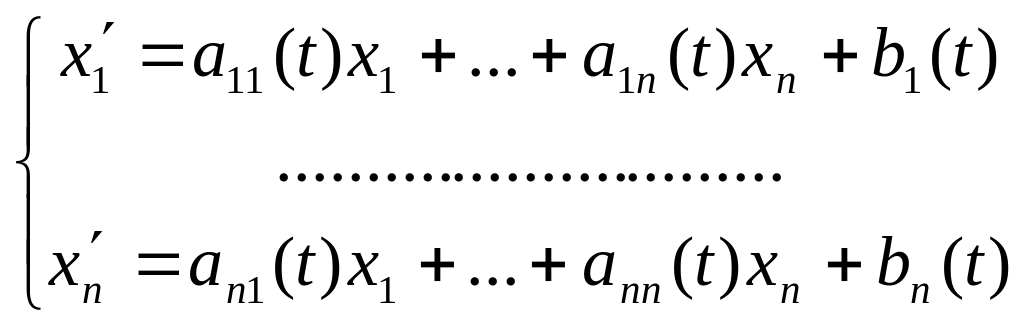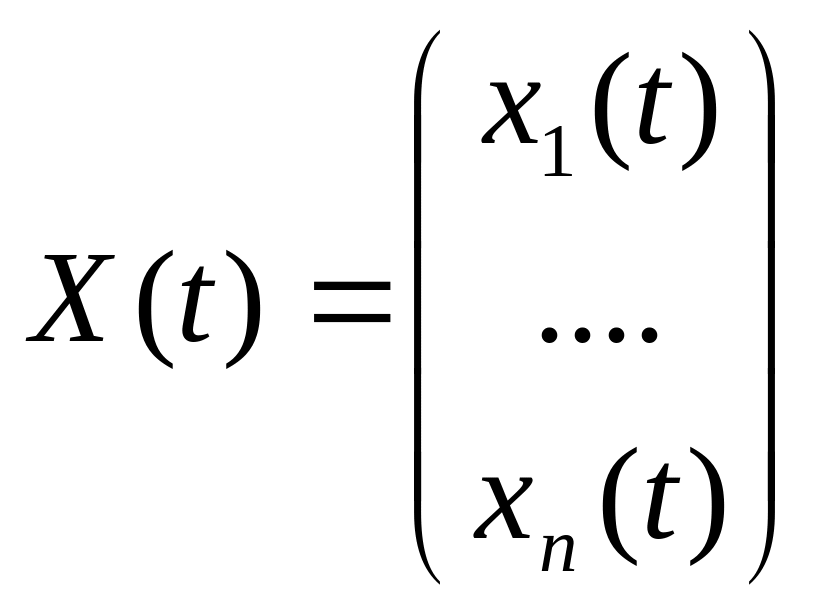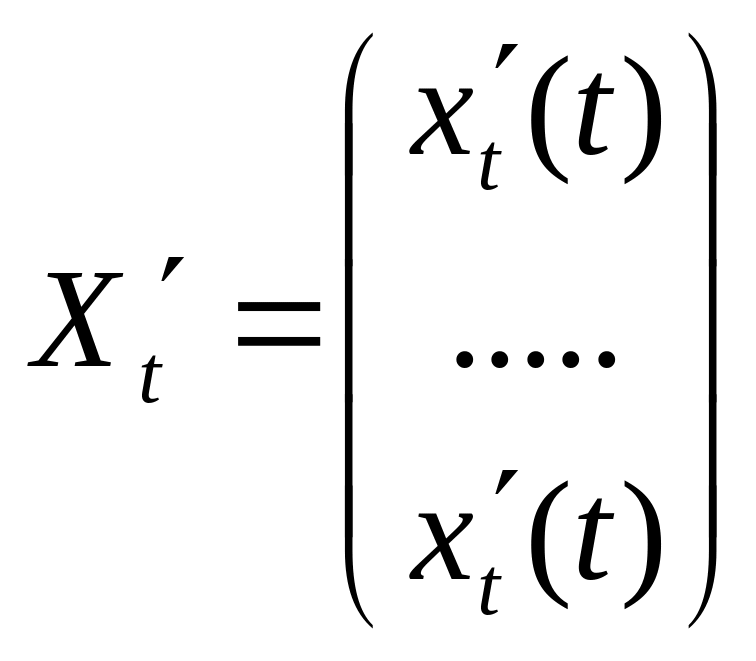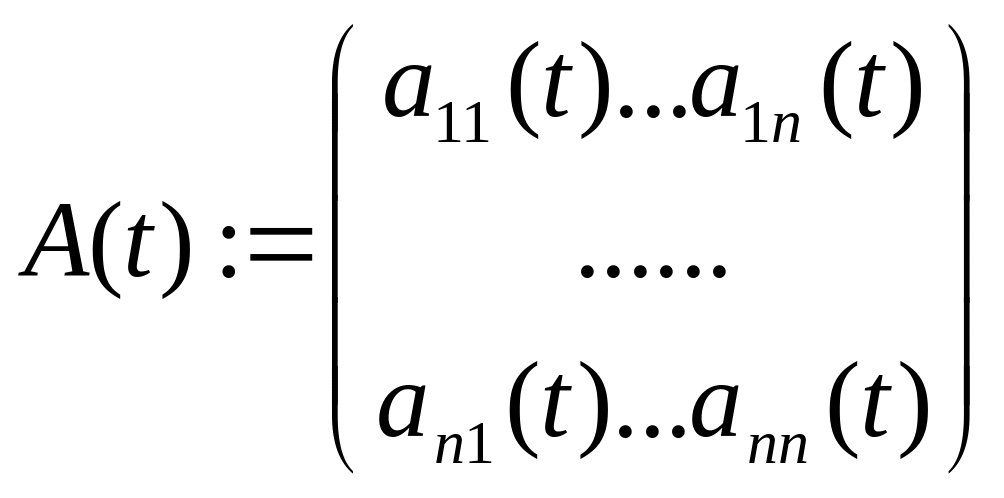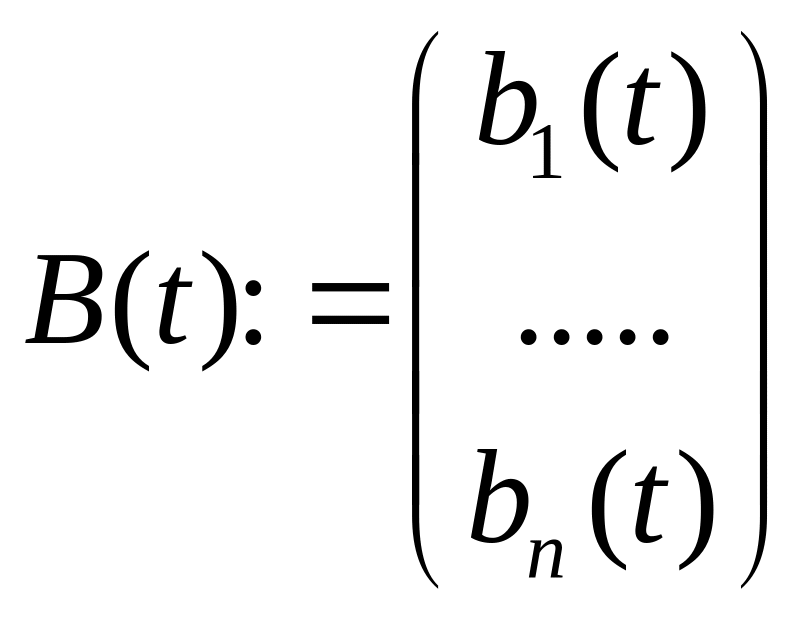Опр Нормальной системой линейных дифференциальных уравнений (НСЛДУ) называется система вида или в матричной форме где - искомое решение на ; ; - матрица непрерывных на коэффициентов; - матрица непрерывных на свободных членов.

Опр НСЛДУ называется однородной, если , и неоднородной в противном случае.

Опр Последовательность решений 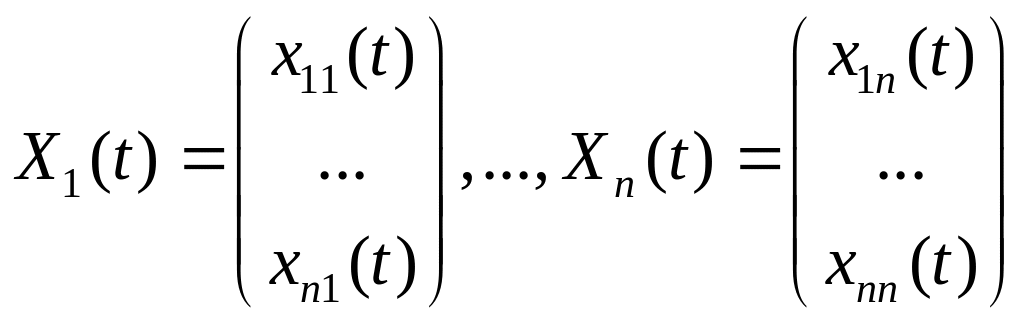однородной

НСЛДУ называется фундаментальной системой, если

векторы линейно независимы.

Опр Определитель и матрица 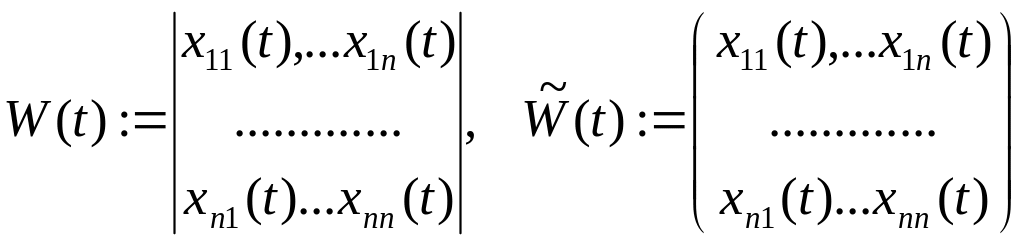называются соответственно вронскианом и фундаментальной матрицей (матрицей Вронского) НСЛДУ.

Последняя есть пример функциональной матрицы.

Опр Производной функциональной матрицы называется функцио нальная матрица ; интегралом функциональной матрицы на отрезке называется числовая матрица .

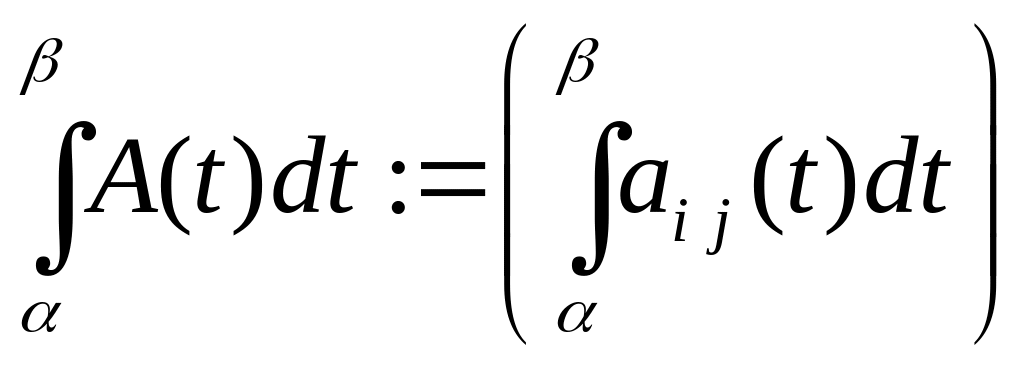Пример .

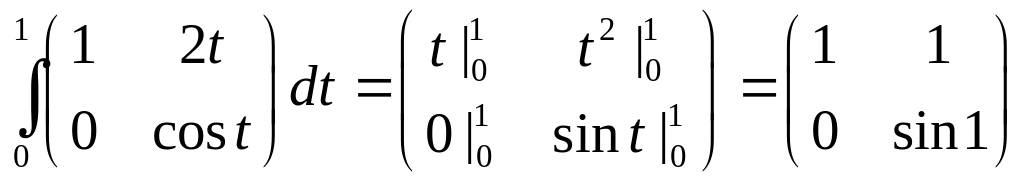ЗАМЕЧАНИЕ 1) Постоянную матрицу-множитель можно выносить за знак инте грала и производной: 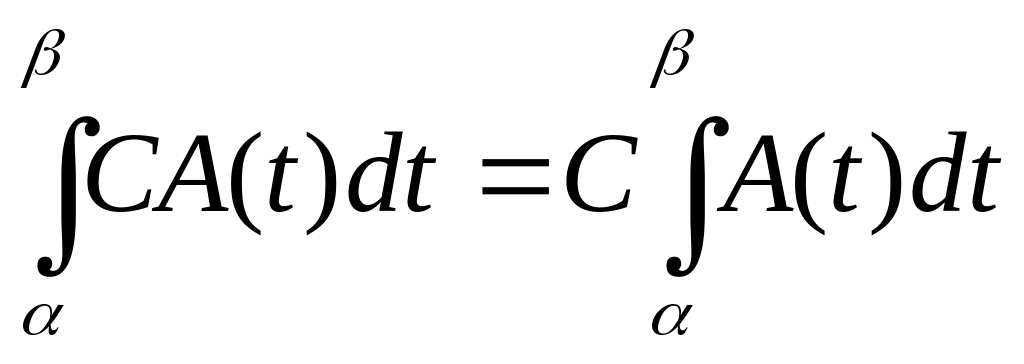, . 2)

ТЕОРЕМА 2 (Свойства решений НСЛДУ) 1)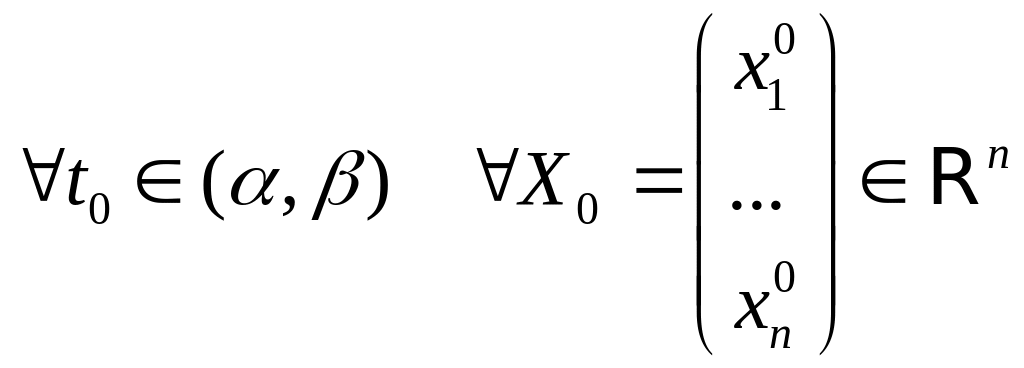 существует един ственное решение на задачи Коши с начальным условием

2) Систем решений фундаментальна на тогда и только тогда, когда ;

3) Если система решений фундаментальна на , то общее решение однородной НСЛДУ имеет вид .

4) Если - какое-либо (частное) решение неоднородной НСЛДУ, то общее (любое) решение этой НСЛДУ имеет вид ,

где - фундаментальная система.

5) Eсли известна фундаментальная система , то частное решение неодно родной НСЛДУ можно вычислить по формуле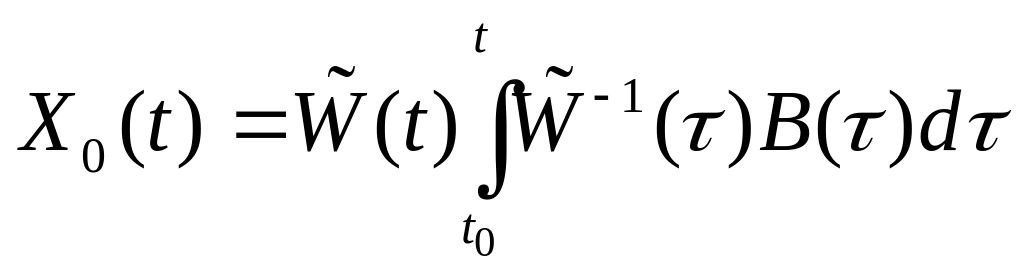 , а решение задачи Коши с начальным условием - по формуле Коши 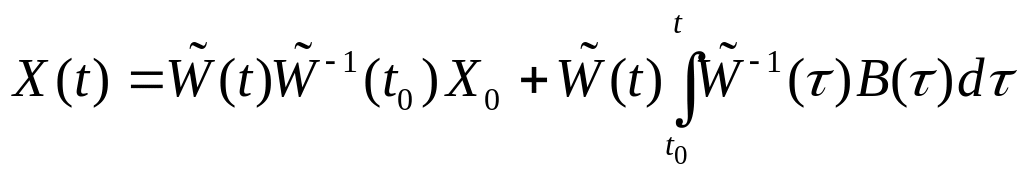, где .

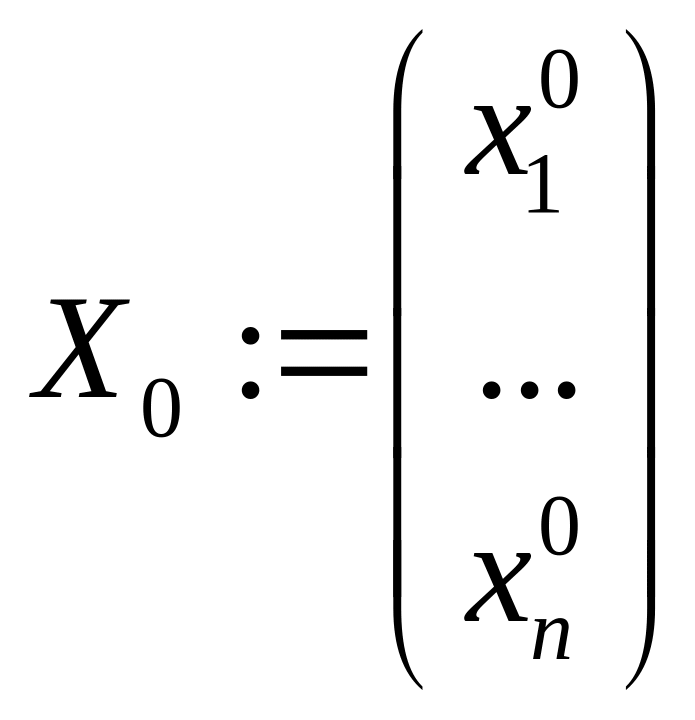Опр Если - фундаментальная матрица НСЛДУ, то матрица называется переходной матрицей этой системы.

ЗАМЕЧАНИЕ 1) Переходная матрица является решением задачи Коши для матричного уравнения с функциональной матрицей размера и начальным условием , где есть единичная матрица.

2) Переходная матрица не зависит от выбора фундаментальной системы и полностью

определяется матрицей коэффициентов НСЛДУ.

3) В обозначениях переходной матрицы формула Коши принимает вид

_____

Опр Линейным дифференциальным уравнением -го порядка (ЛДУ) называется ОДУ вида , (1)

где функции непрерывны на . ЛДУ называется однородным, если и неоднородным в противном случае.

Опр Последовательность решений однородного ЛДУ -го порядка называется линейно независимой на , если не существует такой ненулевой -ки чисел , что на .

Опр Определителем Вронского и фундаментальной матрицей однородного ЛДУ называются соответственно ,

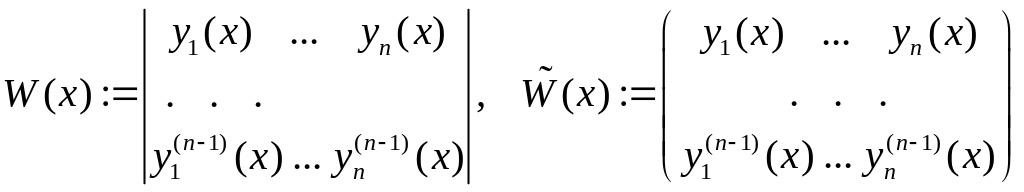где есть последовательности линейно независимых решений (фундаментальная последовательность решении ЛДУ).

ЗАМЕЧАНИЕ Несложно показать, что линейная независимость последовательности решений ЛДУ (1) равносильна тому, что последовательность соответствующих решений 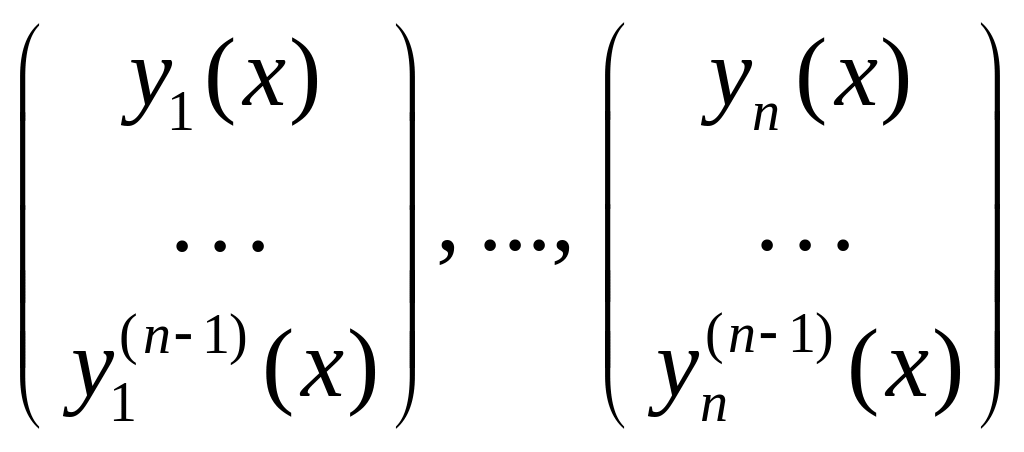ассоциированной с (1) НСЛДУ ,

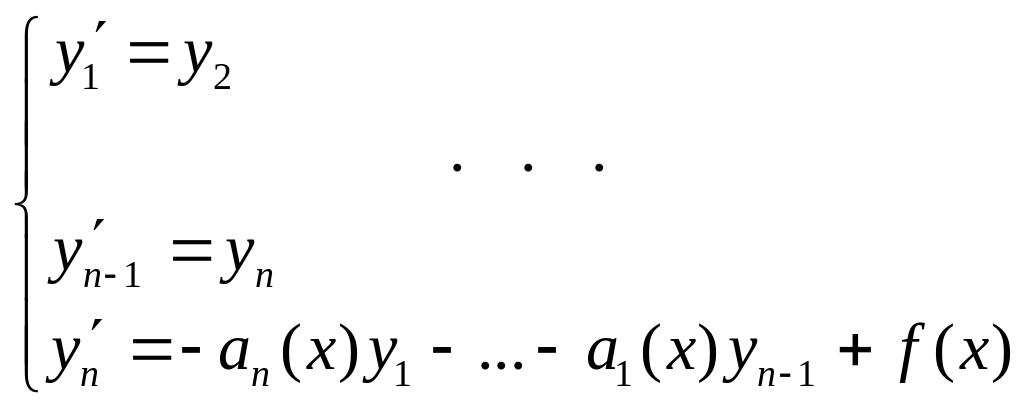является фундаментальной. Поэтому прямым следствием теоремы 2 является

ТЕОРЕМА 3 (свойства решений ЛДУ -го порядка) 1) задача Коши с начальным условием имеет единственное решение на .

2) Решения однородного ЛДУ линейно независимы на тогда и только тогда, когда .

3) Если - фундаментальная последовательность решений однородного ЛДУ, то любое (общее) его решение имеет вид

4) Если -какое-либо решение ЛДУ (1) и - фундаментальная последовательность решений, то любое (общее) решение ЛДУ можно записать в виде .

5) Если известна фундаментальная последовательность , то решение задачи Коши для уравнения (1) можно искать по формуле Коши для этого уравнения

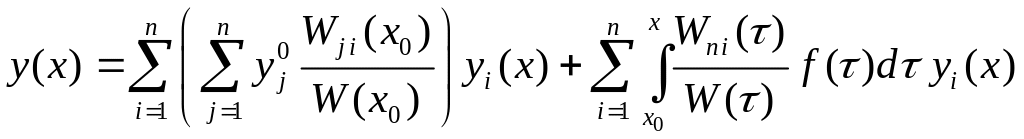, где есть алгебраическое дополнение соответствующего элемента фундаментальной матрицы .

_____

Опр Характеристическим многочленом матрицы мы называется многочлен -ой степени . Нули этого многочлена порядков соответственно назывались собственными числами матрицы . Ненулевые решения, вообще говоря комплекснозначные, СЛАУ

называются собственными векторами матрицы .

ЗАМЕЧАНИЕ Пусть дана НСЛДУ с постоянными коэффициентами

,

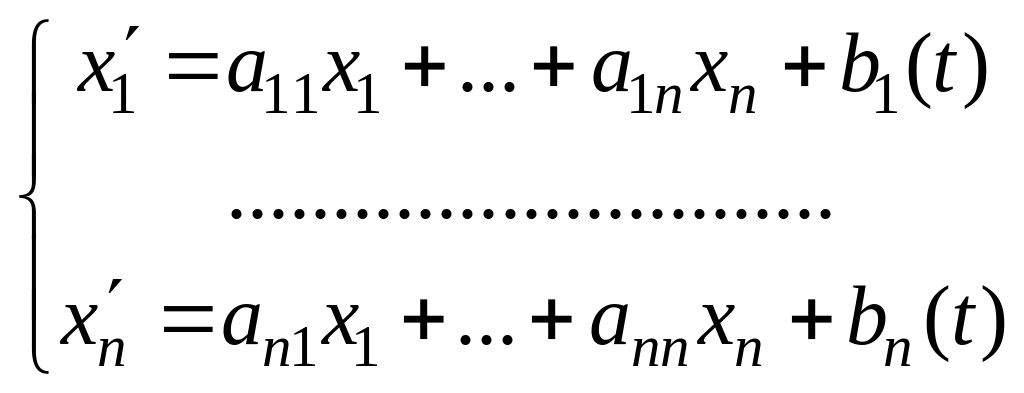и собственные числа ее матрицы коэффициентов попарно различны и вещественны. Обозначим 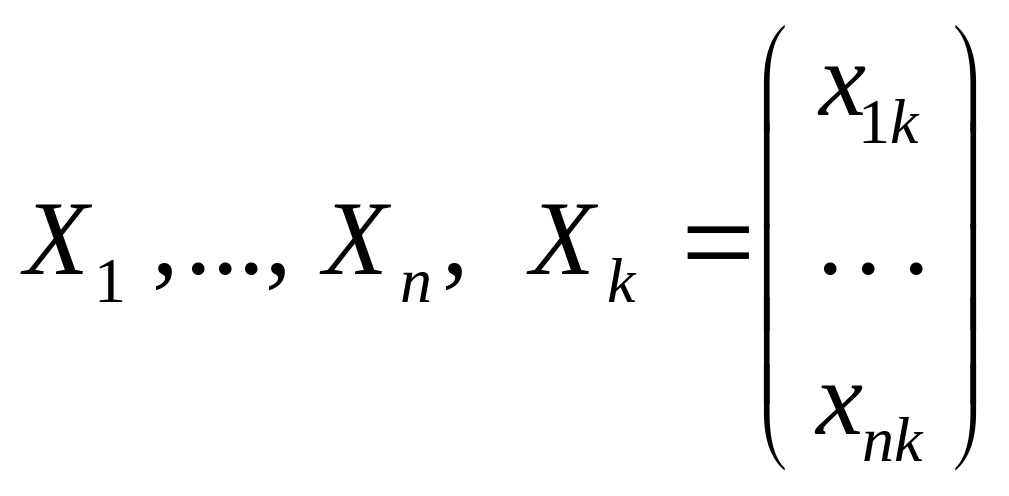, соответствующие им собственные векторы. Тогда:

1) общее решение однородной НСЛДУ имеет вид ;

2) матрица является фундаментальной, и решение задачи Коши однородной НСЛДУ находится по формуле ;

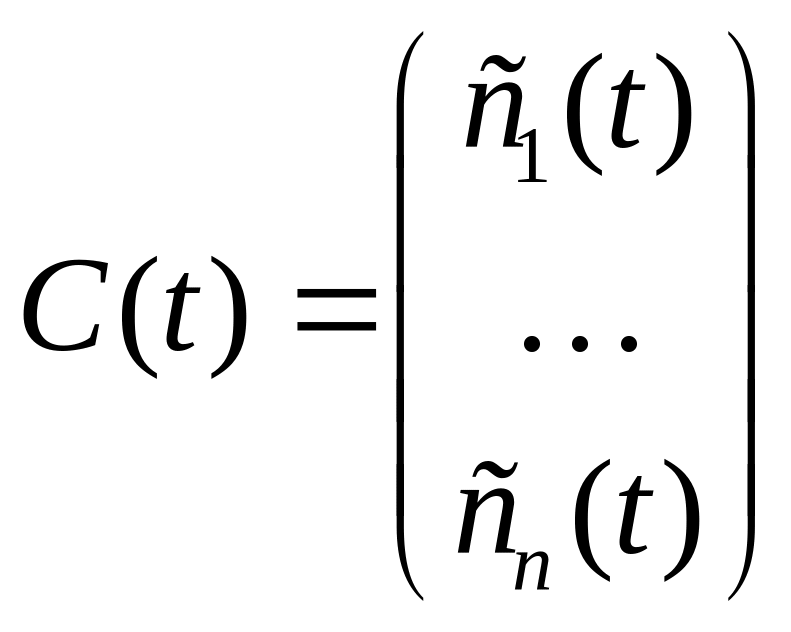3) частное решение НСЛДУ ищется методом вариаций в виде , где есть решение системы дифференциальных уравнений .
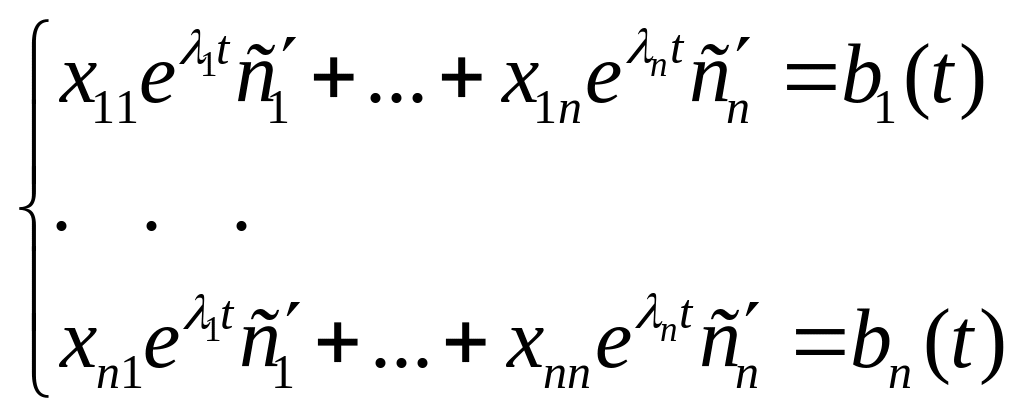