Интегрируемые оду первого и второго порядков

Опр ОДУ вида или вида называется ОДУ с разделяющимися переменными. ОДУ вида или вида называется ОДУ с разделенными переменными.

ЗАМЕЧАНИЕ Решения этих уравнений выписываются в квадратурах:

, .

_____

Опр Функция называется однородной функцией степени , если

.

Пример - однородная функция нулевой степени; - однородная

функция степени .

Опр ОДУ вида или вида называется однородным, если соответственно - однородная функция нулевой степени, - однородные функции одинаковой степени.

ЗАМЕЧАНИЕ Однородное ОДУ преобразуется в ОДУ с разделяющимися перемен ными, если зависимую переменную заменить на по формуле .

_____

Опр ОДУ вида , где функции заданы и непрерывны, называется уравнением Бернулли, если и линейным уравнением (ЛДУ) в противном случае.

ЗАМЕЧАНИЕ Эти ОДУ решаются методом вариации произвольной постоянной. 1) Сначала решается ОДУ с разделяющимися переменными .

.

2) Решение исходного уравнения ищем в виде , считая в предыдущем решении произвольную постоянную зависящей от (говорят: варьируя произвольную постоянную ). Для нахождения подставим это решение в

исходное уравнение: . После сокращения получаем уравнение с разделяющимися переменными для нахождения .

Пример Пусть в фильтре нижних частот входное напряжение изменяется по синусоидальному закону: . Тогда уравнение фильтра нижних частот имеет вид . Так как решение соответствующего однородного уравнения равно , то частное решение ищем в виде. находим из уравнения с разделяющимися переменными

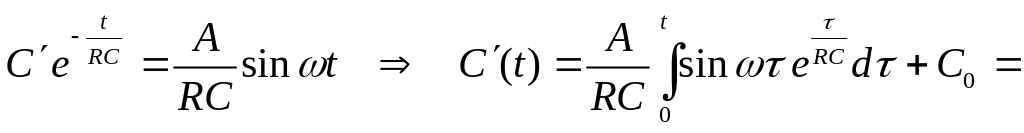
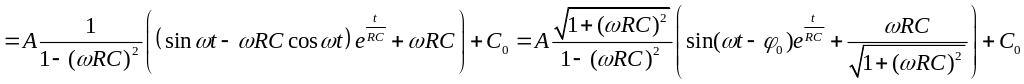где 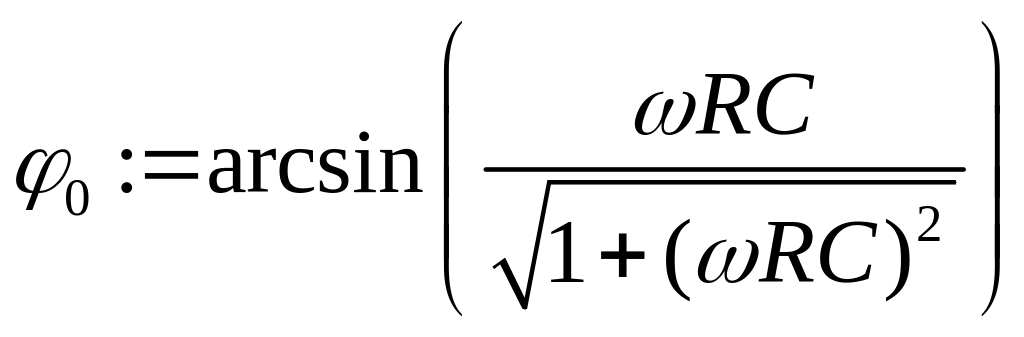. Тогда падение напряжения на конденсаторе изменяется по закону .

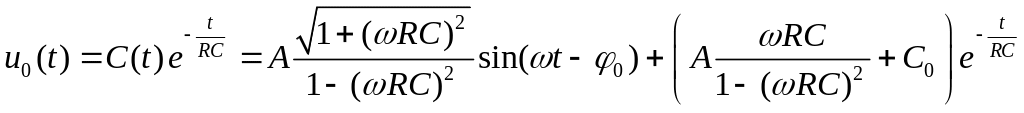С течением времени второе слагаемое стремится к нулю. Поэтому будет меняться периодически. Его амплитуда 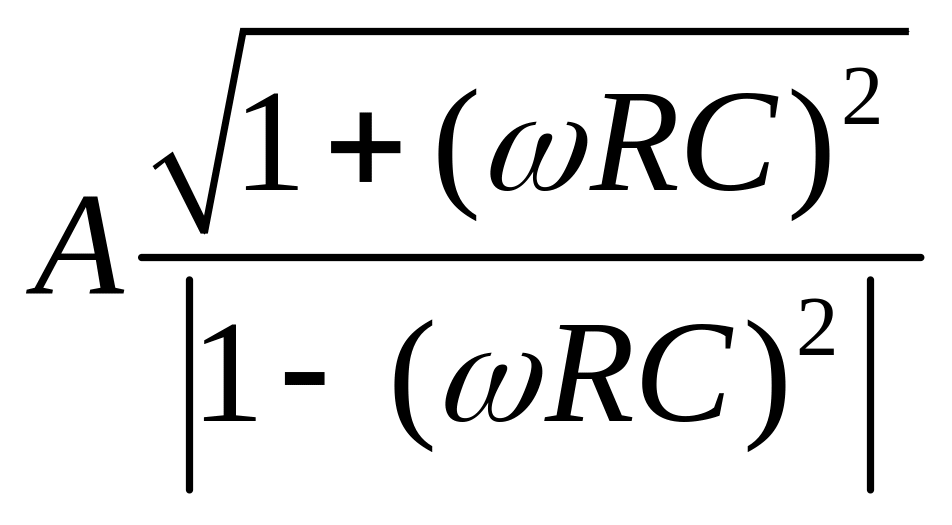, очевидно, мала для больших (верхних) значений частот , что и объясняет название фильтра.

­­­____

ЗАМЕЧАНИЕ 1 Решение ОДУ второго порядка вида сводится к решению ОДУ первого порядка с помощью замены .

ЗАМЕЧАНИЕ 2 Решение ОДУ второго порядка вида сводится к решению

ОДУ первого порядка с помощью замены на зависимую переменную .

Первое очевидное. Докажем второе. .

Пример (Уравнение колебаний математического маятника).

М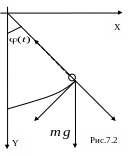 атериальная точка массы подвешена на нерастяжимой нити длины . На неё действуют две силы: вертикальная сила тяжести и сила реакции нити. Запишем закон колебаний маятника в виде

,

где - угол его отклонения от положения равновесия в момент времени. Равнодействующая этих сил направлена по касательной к маятнику и потому второй закон Ньютона для него имеет вид

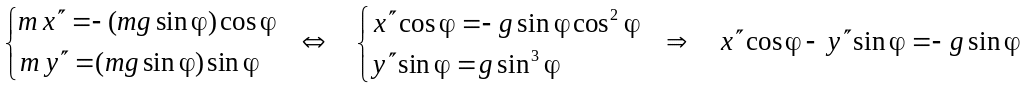Продифференцируем первую систему два раза

.

И мы вывели уравнение колебаний математического маятника

Это ОДУ второго порядка. Понизим его порядок с помощью замены

.

В крайнем левом положении маятника по физическому смыслу имеем

.
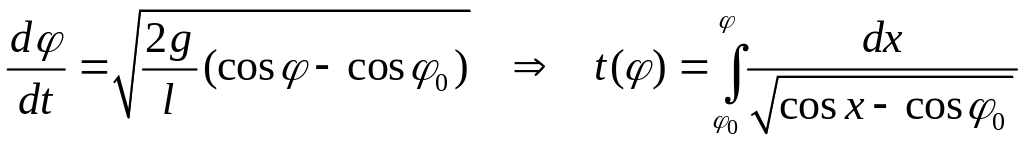