
- •8.Вопросы по теме « ряды и интеграл фурье»
- •8.1Примеры скалярного произведения для функций одной переменной
- •8.4 Определение ряда фурье и его коэффициентов для функций с периодом 2пи
- •8.5 Теорема Дирихле для разложения в ряд Фурье с периодом 2 пи
- •8.6 Ряд Фурье для функции с произвольным интегралом
- •8.7 Ряды Фурье для чётных и нечётных функций.
- •8.9 Комплексная формула для интеграла фурье
- •8.10Представление интеграла Фурье для четных и нечетных функций
- •9.Вопросы по теме «истоки операционного исчисленияы на примере преобразования Фурье»
- •9.1Преобразование Фурье (прямое и обратное) общего вида
- •9.2 Косинус-преобразование Фурье
- •9.3 Синус-преобразование Фурье
- •10 . Вопросы по теме «преобразование лаплпса».
- •11 Вопросы по теме «обыкновенные дифференциальные уравнения».
- •11.3 Понятие интеграла дифференциального уравнения
- •11.4 Задача Коши для дифференцмального уравнения
- •11.6 Понятие однородной функции двух переменных и однородного дифференциального уравнения.
- •11.7Уравнения в полных дифференциалах.
- •11.8 Неменее трех вариантов дифференциального уравнения с методом понижения его порядка
- •11.9 Линейные дифференциальные уравнения второго и высшего порядка Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения высших порядков
- •12 Вопросы по теме «линейные диф-ные уравнения и системы с постоянными коэф-ми»
- •12.3 Метод вариации произвольных постоянных решения линейных неоднородных уравнений
- •12.5 Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами
- •12.6 Метод решения системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами
- •13.Вопросы по теме»ряды и операционное исчисление решении Дифференциальных уравнений и систем
- •13.1Решение задачи Коши с помощью степенных рядов
- •13.2 Базовый подход к поиску общего решения дифференциального уравнения с помощью рядов
- •13.5 Базовый подход к решению задачи Коши для дифференциального уравнения с помощью операционного исчисления
- •13.6 Базовый подход к решению задачи Коши для систем дифференциальных уравнений с помощью операционного исчисления
- •14 Вопросы по теме «понятие статистики»
9.2 Косинус-преобразование Фурье
Преобразование фурье
Пусть
функция f(x) удовлетворяет
условиям интегральной теоремы Дирихле
и является четной функцией, тогда
коэффициент в (16) ![]() .
Представим интеграл Фурье (15) в виде:
.
Представим интеграл Фурье (15) в виде:
 (19)
(19)
 (20)
(20)
Функция
F(![]() ),
определенная формулой (19), называется
косинусом -преобразованием Фурье
для f(x).
),
определенная формулой (19), называется
косинусом -преобразованием Фурье
для f(x).
Формула (20) задает обратное косинус – преобразование Фурье, позволяющее по F(a ) находить f(x).
Аналогично, если f(x) – нечетная функция, то A(a ) = 0, тогда формулы (21) и (22) задают соответственно прямое и обратное синус-преобразование Фурье
 (21)
(21)
 (22)
(22)
Пусть функция f(x) представима интегралом Фурье в комплексной форме (17), а коэффициент С(a ), определенный формулой (18) называется спектральной функцией . Если интеграл Фурье в комплексной форме представить в виде
 (23)
(23)
то функция S(a ) также называется спектральной и S(a ) = 2p C(a ).
Преобразованием
Фурье называется функция ![]() определенная
формулой (24)
определенная
формулой (24)
 ,
(24)
,
(24)
а функция f(x) , определенная формулой (25) называется обратным преобразованием Фурье
 .
(25)
.
(25)
Преобразование Фурье отличается от спектральной функции только множителем
![]()
(![]() также
называется спектральной функцией).
также
называется спектральной функцией).
Если
функция f(x)
– оригинал
с показателем роста ![]() ,
то функция g(x), определенная формулой
,
то функция g(x), определенная формулой ![]() ,
где
,
где ![]() называется
затухающим оригиналом. Тогда для функции
g(x) существует и преобразование Фурье
и преобразование Лапласа и они связаны
между собой формулой
называется
затухающим оригиналом. Тогда для функции
g(x) существует и преобразование Фурье
и преобразование Лапласа и они связаны
между собой формулой
![]() .
(26)
.
(26)
Пример 1.
Для
функции ![]() найти
косинус преобразование Фурье.
найти
косинус преобразование Фурье.
Решение





Тогда косинус - преобразование Фурье функции имеет вид

Пример 2.
Найти
обратное преобразование Фурье для
функции 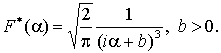
Решение.


![]()

9.3 Синус-преобразование Фурье
(синус-преобразование). Формулы (1), (2) и (3) обратимы, т. е. для чётных функций
![]() ,
(4)
,
(4)
а для нечётных функций
![]() .
(5)
.
(5)
В общем случае имеет место формула
![]() .
.
10 . Вопросы по теме «преобразование лаплпса».
10.1
Преобразова́ние Лапла́са —
интегральное преобразование, связывающее
функцию ![]() комплексного
переменного (изображение)
с функцией
комплексного
переменного (изображение)
с функцией ![]() вещественного
переменного (оригинал).
С его помощью исследуются свойства динамических
систем и
решаются дифференциальные и интегральные
уравнения.
вещественного
переменного (оригинал).
С его помощью исследуются свойства динамических
систем и
решаются дифференциальные и интегральные
уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
10.4/10.5/ 10,6/ 10,7/10.8/ 10,9/10,10
http://math.volchenko.com/Lectures/OC%20Orig.pdf
10.3
Прямое преобразование Лапласа
Преобразованием
Лапласа функции вещественной
переменной ![]() ,
называется функция
комплексной
переменной
,
называется функция
комплексной
переменной ![]() [1],
такая что:
[1],
такая что:

Правая часть этого выражения называется интегралом Лапласа.
[править]Обратное преобразование Лапласа
Обратным
преобразованием Лапласа функции комплексного
переменного ![]() ,
называется функция
вещественной
переменной, такая что:
,
называется функция
вещественной
переменной, такая что:

где ![]() —
некоторое вещественное число (см. условия
существования).
Правая часть этого выражения
называется интегралом
Бромвича.
—
некоторое вещественное число (см. условия
существования).
Правая часть этого выражения
называется интегралом
Бромвича.
Двустороннее преобразование Лапласа
Основная статья: Двустороннее преобразование Лапласа
Двустороннее
преобразование Лапласа — обобщение
на случай задач, в которых для
функции
участвуют
значения ![]() .
.
Двустороннее преобразование Лапласа определяется следующим образом:

