
- •Содержание
- •Глава 1. История развития учения о радиоактивности 7
- •Глава 2. Общие сведения о строении 15
- •Глава 3. Радиоактивный распад 35
- •Глава 4. Виды радиоактивных превращений (физические основы) 57
- •Глава 5. Взаимодействие ионизирующего излучения с веществом 88
- •Глава 6. Детекторы ионизирующих излучений 125
- •Глава 7. Методы измерения ионизирующих излучений 168
- •Глава 8. Статичтическая обработка радиометрических измерений 186
- •Предисловие
- •Глава 1. История развития учения о радиоактивности
- •Глава 2. Общие сведения о строении и свойствах ядер
- •2.1 Элементарные частицы
- •2.2 Свойства атомных ядер
- •2.3 Масса ядра и энергия связи
- •2.4 Вопросы для самоконтроля и задачи для самостоятельного решения
- •2.4.1 Вопросы для самоконтроля
- •2.4.2 Задачи
- •Глава 3. Радиоактивный распад
- •3.1 Основной закон радиоактивного распада
- •3.2 Статистический характер радиоактивного распада
- •3.3 Радиоактивный распад в природе
- •3.4 Последовательный распад радиоактивных ядер. Радиоактивное равновесие
- •3.5 Определение периода полураспада
- •3.6 Определение возраста минералов
- •3.7 Вопросы для самоконтроля и задачи для самостоятельного решения
- •3.7.1 Вопросы
- •3.7.2 Задачи
- •238U (4,51109 лет) → 234Th (24,1 суток) →.
- •Глава 4. Виды радиоактивных превращений (физические основы)
- •4.1 Альфа-распад
- •4.2 Бета-распад
- •4.2.1. Особенности бета-распада
- •4.2.2 Схемы бета-распада
- •4.2.3 Условия бета-распада
- •4.2.4 Бета-спектр и факторы, влияющие на его формирование
- •4.3 Фотонное излучение
- •4.3.1 Гамма-излучение
- •4.3.2 Место гамма-излучения в электромагнитном спектре
- •4.3.3 Рентгеновское излучение
- •4.4 Спонтанное деление ядер
- •4.5 Вопросы для самоконтроля
- •Глава 5. Взаимодействие ионизирующего излучения с веществом
- •5.1 Взаимодействие альфа-частиц с веществом
- •5.2 Взаимодействие электронов и позитронов с веществом
- •5.3 Черенковское излучение
- •5.4 Взаимодействие гамма-квантов с веществом
- •5.4.1 Фотоэффект
- •5.4.2 Комптоновское рассеяние γ-квантов
- •5.4.3 Эффект образования пары
- •5.4.4 Ослабление гамма-излучения в веществе
- •5.5 Вопросы для самоконтроля и задачи для самостоятельного решения
- •5.5.1 Вопросы
- •5.5.2 Задачи
- •Глава 6. Детекторы ионизирующих излучений
- •6.1 Газонаполненные ионизационные детекторы
- •6.1.1 Ионизационные камеры
- •6.1.2 Пропорциональные счетчики
- •6.1.3 Счетчики Гейгера-Мюллера
- •6.2 Сцинтилляционные детекторы
- •6.2.1 Основные характеристики сцинтилляторов
- •6.2.2 Основные виды и типы сцинтилляторов
- •6.2.3 Фотоэлектронные умножители (фэу)
- •6.3 Полупроводниковые (твердотельные) детекторы
- •6.3.1 Физические основы полупроводниковых детекторов
- •6.3.2 Принцип действия полупроводниковых детекторов
- •6.3.3 Типы полупроводниковых детекторов
- •6.4 Вопросы для самоконтроля
- •Глава 7. Методы измерения ионизирующих излучений
- •7.1 Радиометрия
- •7.1.1 Абсолютная и относительная активность
- •7.1.2 Радиометр как цепь измерительных преобразователей
- •7.2 Спектрометрия
- •7.2.1 Гамма-спектрометрия
- •7.2.2 Альфа-спектрометрия
- •7.3 Вопросы для самоконтроля
- •Глава 8. Статичтическая обработка радиометрических измерений
- •8.1 Общие положения
- •8.2 Распределение Пуассона при радиометрических измерениях
- •8.3 Погрешность скорости счета
- •8.4 Определение необходимого времени проведения радиометрических измерений с заданной точностью
- •8.5 Проверка правильности работы счетной аппаратуры
- •8.6 Оценка погрешности результата вычислений
- •8.7. Вопросы для самоконтроля
- •Рекомендованная литература
- •Приложение Радиоактивные семейства
5.1 Взаимодействие альфа-частиц с веществом
Альфа-частицы, как и другие тяжёлые заряженные частицы (например, протоны, дейтоны) взаимодействуют, главным образом, с орбитальными электронами атомов, вызывая их ионизацию и возбуждение. Вероятность же протекания ядерных реакций (см. главу 5) при энергиях альфа-частиц, испускаемых радиоактивными ядрами (до 9 МэВ), примерно в 103 раз меньше и зависит от заряда ядер материала.
Проходя через
вещество, альфа-частица совершает
десятки тысяч соударений, постепенно
теряя энергию. Из законов механики
следует, что максимальная энергия,
которую может получить атомарный
электрон при взаимодействии с α-частицей,
равна
![]() .
Благодаря значительной массе α-частицы
траектория ее движения в веществе
практически не отклоняется от
первоначального направления (рисунок
5.1).
.
Благодаря значительной массе α-частицы
траектория ее движения в веществе
практически не отклоняется от
первоначального направления (рисунок
5.1).

Рис. 5.1. Траектория движения альфа-частиц в веществе и процесс ионизации среды.
Тормозная способность
вещества может быть охарактеризована
величиной удельных
потерь энергии
![]() ,
где dE
- энергия,
теряемая частицей в слое вещества
толщиной dx.
Если энергия заряженной частицы теряется
на ионизацию среды, то говорят об удельных
ионизационных потерях. Удельная ионизация
не является постоянной величиной, а
зависит от пройденного расстояния
альфа-частицей. Если измерить зависимость
удельной ионизации от расстояния,
пройденного частицей, то получится
кривая, показанная на рисунке 6.2.
,
где dE
- энергия,
теряемая частицей в слое вещества
толщиной dx.
Если энергия заряженной частицы теряется
на ионизацию среды, то говорят об удельных
ионизационных потерях. Удельная ионизация
не является постоянной величиной, а
зависит от пройденного расстояния
альфа-частицей. Если измерить зависимость
удельной ионизации от расстояния,
пройденного частицей, то получится
кривая, показанная на рисунке 6.2.
Альфа-частицы обладают очень большой ионизирующей способностью, и поэтому теряют свою энергию на поглощение в сравнительно тонких слоях материала поглотителя. Ионизационные потери α-частиц, а также протонов, дейтонов и др. тяжелых частиц , пропорциональные числу электронов в 1 см3 поглотителя и обратно пропорциональные энергии частицы, вычисляются по уравнению:
![]() , (5.1)
, (5.1)
где
![]() – кинетическая энергия нерелятивистской
частицы (все альфа-частицы, испускаемые
радионуклидами, имеют кинетическую
энергию меньше 9 МэВ и поэтому не
являются релятивисткими);
– кинетическая энергия нерелятивистской
частицы (все альфа-частицы, испускаемые
радионуклидами, имеют кинетическую
энергию меньше 9 МэВ и поэтому не
являются релятивисткими);
![]() и
v
– заряд и скорость частицы;
и
v
– заряд и скорость частицы;
N – число атомов в 1 см3;
Z – эффективный заряд материала, так что ZN – среднее число электронов в 1 см3;
![]() и m
– заряд и
масса электрона;
и m
– заряд и
масса электрона;
I – средний ионизационный потенциал.
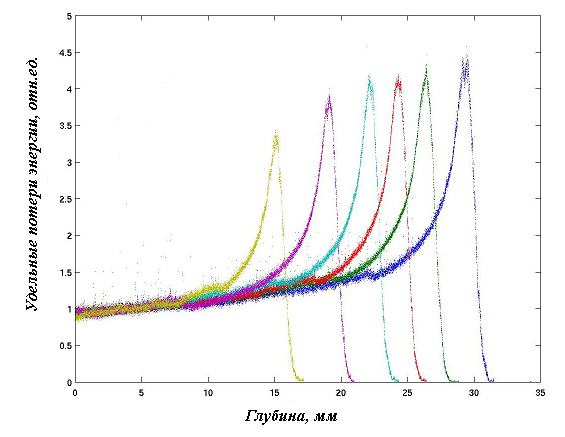
Рис. 5.2. Кривая Брега для α-частиц с различной энергией.
На образование одной пары ионов в воздухе -частица теряет примерно 33,85 эВ. Т.е., если начальная кинетическая энергия -частицы равна 4 МэВ, то она полностью затормозится с образованием 4106/33,85 1,18·105 пар ионов.
Уравнение (6.1) показывает, что ионизационные потери частицы растут с уменьшением ее кинетической энергии и при одинаковой энергии пропорциональны квадрату заряда частицы.
Пробег α-частиц
Альфа-частицы, имеющие одинаковую энергию, проходят в среде до полного замедления практически одно и то же расстояние. Зависимость числа частиц, прошедших определенный слой вещества, от толщины слоя имеет форму кривой (интегральная кривая), представленной на рисунке (рис. 5.3). Дифференциальная кривая отражает число α‑частиц в единицу времени, которые проходят расстояние от источника, лежащее в пределах от Rср до Rср + dR. Дифференциальная кривая совпадает по форме с кривой Гаусса. Максимум этой кривой приходится на величину среднего пробега частиц Rср. Разброс пробега называется страгглингом.
Если экстраполировать наклонный линейный участок интегральной кривой до оси абсцисс, то мы получим экстраполированный пробег α-частиц в веществе Rэ, который всегда больше чем, средний.
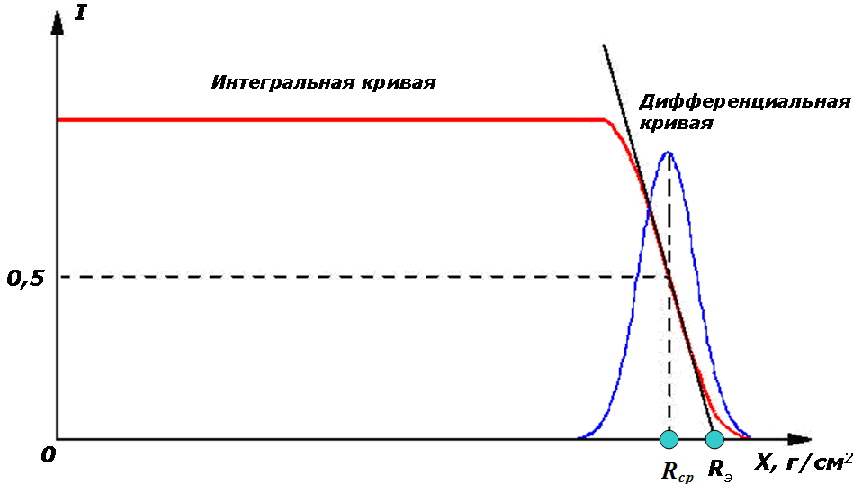
Рис. 5.3. Кривые интегрального и дифференциального распределения пробегов альфа-частиц для тонкого источника.
Разница между экстраполированным и средним пробегом составляет приблизительно 1 % от полного пробега альфа-частиц с энергией 5 МэВ.
Между пробегом альфа-частиц в воздухе и их энергией были установлены эмпирические соотношения. Так, например, средний пробег в воздухе при комнатной температуре и нормальном давлении для -частиц с энергией 210 МэВ связан с энергией Eα в МэВ эмпирической формулой:
![]() . (5.2.)
. (5.2.)
При меньших энергиях
величина пробега оказывается
пропорциональной
![]() ,
а при более высоких энергиях –
,
а при более высоких энергиях –
![]() .
.
Разброс пробегов
зависит от нескольких причин. Во-первых,
флуктуация числа атомов на пути частицы.
Если среднее число ионов, образуемых
α-частицей на длине ее пробега
![]() ,
то возможное отклонение от этого числа,
согласно статистическому закону, равно
,
то возможное отклонение от этого числа,
согласно статистическому закону, равно
![]() .
Среднее число пар ионов, образуемых
-частицей
с энергией 4 МэВ, равно 1,14·105
ионов.
Флуктуация этого значения составит
=338,06,
что составляет 0,3 %. Однако реальные
изменения в пробегах частиц значительно
выше.
.
Среднее число пар ионов, образуемых
-частицей
с энергией 4 МэВ, равно 1,14·105
ионов.
Флуктуация этого значения составит
=338,06,
что составляет 0,3 %. Однако реальные
изменения в пробегах частиц значительно
выше.
Второй причинной, вызывающей страгглинг, является перезарядка частиц при их движении через среду. При прохождении α‑частиц через вещество к ним может примкнуть один или два электрона. Таким образом, на всем пути частица имеет разный заряд. Опытным путем было установлено, что быстрая альфа-частица движется, в основном, как двухзарядный ион, при уменьшении скорости она будет терять заряд, двигаясь как однозарядный ион или даже как нейтральная частица. В результате перезарядка вызывает дополнительные флуктуации в ионизации, а значит и в величине пробега. Эта величина дает 1,5-1,7 % разброса пробегов.
Пробеги альфа-частиц и протонов в некоторых средах приведены в таблице 5.1.
Таблица 5.1 – Пробег альфа-частиц в различных веществах в зависимости от энергии Еa
Вещество |
Еа, МэВ |
||||||
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
|
Воздух, см |
2,5 |
3,5 |
4,6 |
5,9 |
7.4 |
8,9 |
10,6 |
Al, мкм |
16 |
23 |
30 |
38 |
48 |
58 |
69 |
Биологическая ткань, мкм |
31 |
43 |
56 |
72 |
91 |
110 |
130 |
Отношение пробегов для двух веществ, представленных в табл. 6.1, практически не зависят от энергии частицы и определяется отношением электронных плотностей ZN в уравнении (5.1). Для элементов значение
![]() , (5.3)
, (5.3)
где A – атомная масса;
ρ – плотность;
NА – число Авогадро.
Отношение Z/A для легких элементов близко к 0,5 и уменьшается до 0,39 для урана. Другим исключением является водород, для которого оно равно 1. Для водородсодержащих веществ максимальное значение у метана – 0,625, а других меньше: полиэтилен – 0,57, вода – 0,56 и т.д. Таким образом, с точностью не хуже 20 % можно принять, что
![]() ,
(5.3а)
,
(5.3а)
а произведение R·ρ (размерность г/см2) с точностью до 20 % является инвариантным и не зависит от природы вещества.
