Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТФКП.doc

Скачиваний:

Добавлен:

13.09.2019

Размер:

453.12 Кб

Скачать

☆

1. Комплексные числа: основные определения, геометрическая иллюстрация:

Алгебраїчна форма комплексного числа: z=x+iy.

При цьому x називається дійсною частиною z (x=Re z), y – уявною частиною z (y=Im z), i – уявною одиницею (i² = -1).

Якщо z=x, (y=0) → z – дійсне число.

Якщо z=iy, (x=0) → z – чисто уявне число.

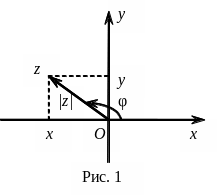
Комплексне число z=x+iy зображується точкою (або радіус-вектором) з координатами (x; y) на комплексній площині (рис. 1), при цьому вісь Ох називається дійсною віссю, а вісь Оу – уявною.

Спряжене комплексне число: , для z=x+iy.

У мова рівності двох комплексних чисел z₁, z₂ в алгебраїчній формі:

А ргумент z — це кут, утворений радіус-вектором, що зображує число z, з додатнім напрямом осі Ox. Для числа z=0 поняття аргументу не має змісту; для z 0 аргумент визначається неоднозначно:

, де, — головне значення аргументу.

М аючи число z, записане в алгебраїчній формі, головне значення аргументу z можна обчислити за формулою:

Р озглядаючи полярні координати точки, яка відповідає комплексному числу z=x+iy , дістанемо число z, записане у тригонометричній формі:

С пряжене :

П оказникова форма комплексного числа:

С пряжене :

У мова рівності двох комплексних чисел z₁, z₂ в тригонометричній формі:

2. Операции над комплексными числами:

Д одавання (віднімання) комплексних чисел зручніше виконувати в алгебраїчній формі; при цьому якщо z₁=x₁+iy₁, z₂=x₂+iy₂, то

М ноження і ділення комплексних чисел часто зручніше виконувати в тригонометричній або показниковій формах; при цьому якщо

т о

А якщо

, .

П іднесення до степеня зручніше виконувати, якщо z записане в тригонометричній формі (формула Муавра):

Корінь п-го степеня із має n різних значень, які знаходять за формулою:

3. Понятие области на комплексной плоскости. Граница области. Порядок связанной области:

Областью на множестве – называется множество точек на плоскости + свойства открытости и связности.

Открытость: любая точка множества принадлежит ей вместе с некоторым своим околом.

Связность: любые две точки этого множества можно соединить линией, что полностью состоит только с точек этого множества.

Точка, которая сама не принадлежит области, но любая ее окрестность содержит точки этой окрестности, называется граничной точной.

Совокупность граничных точек области называется граничной областью.

Область называется ограниченной, если ее можно заключить в некоторый круг конечного радиуса.

Для замкнутых областей, порядок связной области - называется число связных элементов границы этой области.

4. Понятие функции комплексной переменной. Предел функции:

Термин комплексная функция может относиться к двум видам функций:

К омплекснозначная функция: Комплекснозначная функция — функция вещественного переменного, имеющая комплексные значения:

, где u(x), v(x) – вещественные функции. Функция u(x) называется вещественной частью функции f(x) , а v(x) — её мнимой частью.

Ф ункция комплексного переменного: Это понятие — обобщение предыдущего варианта:

, однако здесь имеется более глубокая связь между u и v.

П онятие предела для последовательности и функции вводится так же, как и в вещественном случае, с заменой абсолютной величины на комплексный модуль. Если

Верно и обратное: из существования пределов компонент вытекает существование предела самой функции, и компонентами предела будут пределы компонентов. Непрерывность комплексной функции тоже определяется так же, как в вещественном случае, и она равносильна непрерывности обеих её компонент.

5 . Показательная и логарифмическая функции комплексной переменной:

П оказникова функція:

Свойства:

- при z=x, x є R , y = 0: exp x = e^x - совпадает

- при z=iy, y є R, x = 0: exp(iy) = e^x(cos y +i sin y)

- exp z₁*exp z₂=exp(z₁+z₂), exp z₁/ exp z₂= exp(z₁-z₂)

- Периодическая, T = 2πi

Логарифмическая функции:

Свойства:

- при z=x, x є R , y = 0: Ln(z)=ln(z), (так как exp x ↔ e^x)

- определена

- многозначная (так как exp w - периодичная)

- Все значения Ln (z):

де — головне значення логарифмічної функції.

6. Тригонометрические функции комплексной переменной:

Свойства:

- при z=x, x є R – совпадают с соответствующими функциями вещественной переменной.

- sin (-z) = -sin (z); cos (-z) = cos (z);

- T (sin z / cos z) = 2π; T (tg z / ctg z) = π;

- сохраняются все формулы тригонометрии

- не обмежені

7. Гиперболические функции комплексной переменной:

Свойства:

- - при z=x, x є R – совпадают с соответствующими функциями вещественной переменной.

- sh (-x) = -sh(x); ch(-x)=ch(x);

- T (sh x / ch x) = 2πi; T (th x / cth x) = πi;

- связь с тригоном. функциями: sin (iz) = ish(z);

cos (iz) = ch(z);

8 . Определение степени с комплексным показателем:

П усть :

З агальна степенева функція:

- при співпадає з zⁿ (однозначна)

- співпадає з (n - значень)

- при - безкінечно-значна.

З агальна показникова функція:

багатозначна.

П ри k = 0:

головне значення.

9. Дифференцируемость функции комплексной переменной. Понятие функции аналитической в точке и функции аналитической в области:

Основні властивості аналітичної функції:

- якщо f (x) та g(x) – аналітичні в точці, то f(x)+g(x), f(x)*g(x) – аналітичні в z_0.

- f(x)/g(x) – аналітична в точці z₀, якщо g(x) 0;

- якщо g(x) – аналітична в z₀ та f(w) – аналітична в w₀ = g(z₀), то f(g(z)) – аналітична в z₀ .

10. Критерий Коши-Римана. Условие Коши-Римана в полярных координатах. Выражение для производных:

11. Интеграл от функции комплексной переменной по контуру. Основные свойства. Формула Ньютона – Лейбница:

Основні властивості інтеграла:

- Лінійність: якщо

- Адетивність:

- Якщо Г_- - крива Г, але з протилежним напрямком обходу, то

- Оцінка інтеграла:

- Якщо довжина кривої, то

- Зведення до інтегралу по дійсній змінній, але від функції комплексної змінної:

12. Теорема Коші для однозв’язної області. Теорема Коші для багатозв’язної області (про складений контур).

13. Интегральная формула Коши и формула Коши для производных аналитических функций.

14. Теоремы Лиувилля и Морера:

Т еорема Лиувилля об ограниченных целых аналитических функциях: если целая функция f(z) комплексных переменных z = (z₁,...,z_n) ограничена, то есть , то f(x) – есть константа.

Теорема Мореры может быть сформулирована так:

Е сли функция f(z) комплексного переменного z в области D непрерывна и интеграл от неё по любому замкнутому спрямляемому контуру равен нулю, то есть

, то f(z) – аналитическая функция в D.

15. Ряд Лорана функции комплексной переменной. Теорема Лорана:

Р яд Лорана — двусторонне бесконечный степенной ряд по целым степеням z – z₀,то есть ряд вида

Э тот ряд понимается как сумма двух рядов:

- это главная часть ряда Лорана.

- это правильная часть ряда Лорана.

Т еорема Лорана: Любая однозначная аналитическая функция f(z) в кольце

представима в D сходящимся рядом Лорана.

16. Нули аналитической функции:

Т очка z₀ – називається нулем аналітичної функції f(z) в деякому околі, якщо z₀ належить цьому околу та

Н улем порядку k аналітичної функції f(z) в деякому околі цієї точки – називається точка z₀ для якої справедливе представлення

д е g(z) – аналітична в z₀ та

Порядок нуля в точці z₀ можна розглядати як номер першої з послідовно знайдених похідних функції в цій точці, що не дорівнює нулю.

17. Классификация изолированных особых точек аналитической функции:

Выделяют 3 типа изолированных особых точек:

- устранимая особая точка

- полюс

- существенно особая точка

18. Определение устранимой особой точки:

И золированная особая точка z₀ называется устранимой особой точкой функций f(z) если существует конечный предел

Теорема: Точка z₀ является устранимой особой точкой функции f(z) тогда и только тогда, когда главная часть ряда Лорана тождественно равняется нулю.

19. Определение полюса. Порядок полюса:

И золированная особая точка z₀ называется полюсом, если

Точка z₀ называется полюсом порядка k, тогда и только тогда, когда она является для функции

нулем порядка k.

Т еорема: Изолированная особая точка z₀ называется полюсом порядка k функции f(z) тогда и только тогда, когда в главной части ряда Лорана было конечное число отличных от нуля членов. При этом высшая отрицательная степень

будет порядком полюса в окрестности точки z₀_.

2 0. Теоремы о представлении функции в окрестности полюса. Связь с нулями:

П усть и z₀ - ноль порядка m₁ для f(z₁), z₀ - ноль порядка m₂ для f(z₂). Тогда, если m₁ > m₂, то z₀ – устранимая особая точка для f(z). А если m₁ < m₂, то z₀ – полюс порядка ( m₂ - m₁) для f(z).

21. Определение существенно особой точки:

И золированная особая точка z₀ называется существенной особой точкой функции f(z), если

- не существует.

Теорема: Точка z₀ является существенной особой точкой функции f(z) тогда и только тогда, когда главная часть ряда Лорана этой функции содержит бесконечное число слагаемых.

22. Определение вычета. Основная теорема о вычетах:

В ычетом функции f(z) в точке z₀ называется коэффициент С_-1 то есть с соответствующего ряда Лорана: