§4 Методы решения теплофизических задач.

При решении любой задачи стремятся установить количественные закономерности между исходными параметрами искомыми величинами.

Для установления такой зависимости необходимо прежде всего установить параметры,от которых эти величины зависят,а для этого необходимо исследовать механизм процесса.

При определении механизма необходимо схематизировать явления,т.е. исключить из рассмотрения второстепенные факторы и оставить лишь основные.

Количественные закономерности между параметрами и искомыми величинами устанавливаются 2 путями: теоретическим и эксперементальным.

Теоретический метод решения задач.

Сначала устанавливается механизм процесса, затем на базе механизма устанавливаются основные математические закономерности процесса и затем на базе основных законов составляются дифференциальные уравнения, которые в дифференциальной форме связывают искомые величины с независимыми переменными.

Далее формулируются основные однозначности,затем дифференциальное уравнение решается, причем с учетом условия однозначности.

Полученные таким путем зависимости представляют искомое решение задачи. Для проверки теоретического решения обычно ставится несколько экспериментов.

Однако диф-ое уравнение Фурье-Кирхгофа и Новье-Стокса в общем виде ( когда рассматривается трехмерное пространство и нестационарные процессы) неразрешимы. Поэтому при теоретическом решении рассматриваются только простые, схематизированные задачи.

Однако чрезмерная схематизация явлений приводит к решению, которое является слишком упрощенным.

Таким образом, математический метод позволяет рассмотреть задачу в общем виде, т.е. весь класс явлений распространения тепла путем математической постановки задачи.

Однако, как правило, при теоретическом методе невозможно решить диф-ое уравнение, иначе говоря, невозможно выделить из класса явлений одно единичное явление.

Экспериментальный метод.

Этот метод позволяет с большой достоверностью исследовать конкретное единичное явление. Но результаты исследования не могут быть распространены на другие явления, которые чем-либо отличаются от первого.

Лучшие стороны экспериментального и теоретического методов объединяются в теорию подобия.

Глава 3. Теория подобия

§1 Сущность подобия.

Теория подобия – это метод научного обобщения экспериментальных данных.

Теория подобия оперирует вместо обычных обобщенными переменными.

Пусть мы ищем следующие зависимость.

Необходимо задать размеры тела X, Y, Z.

Необходимо иметь физические параметры λ, с, а….

Должны иметь дополнительно начальные условия :

Необходимо определить граничные условия. В теории подобия вводится обобщенная температура и другие обобщенные величины.

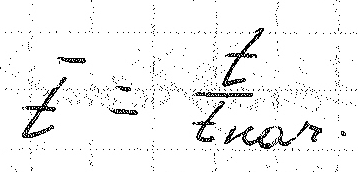( безразмерная велечина.)

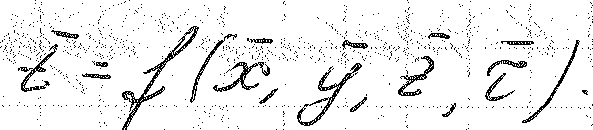
Обобщенные комплексы имеют нулевую размерность и находятся непостредственно из математической постановки задачи и для этого не требуется решать дифференциальные уравнения.

Такого рода уравнения относятся к группе явлений, которая уже понятия класса явлений, но шире понятия единичного явления. В группу входят так называемые, подобные явления.

Выделение группы явлений из класса достигается путем соответствующего задания условий однозначности.

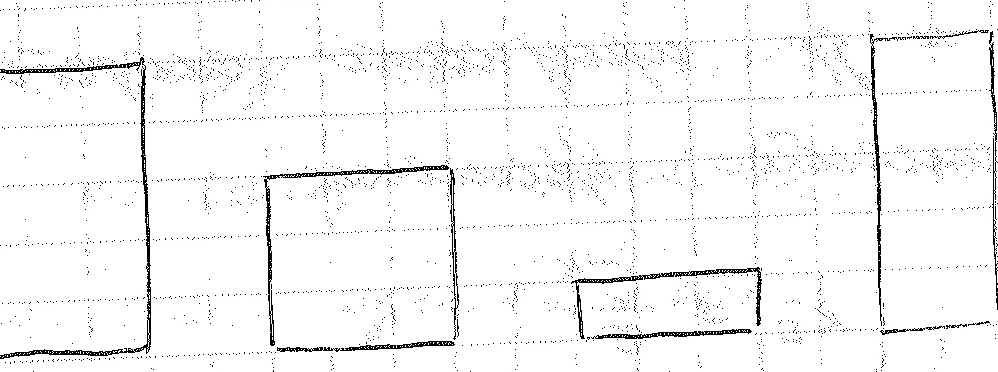Из этих фигур необходимо выбрать группу подобных фигур.

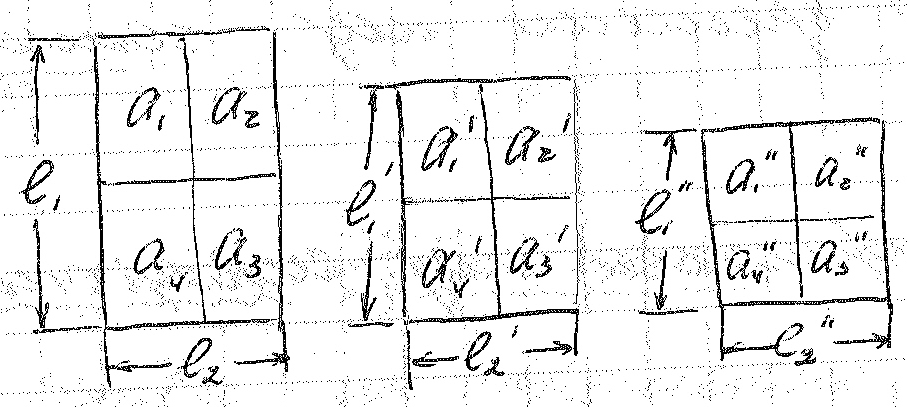
множитель преобразования.

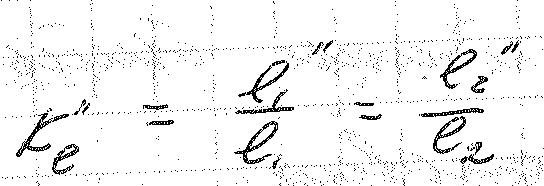
Выбранные фигуры подобны по геометрическим признакам. Теперь из фигур подобных по геометрическим признакам выберем фигуры подобные по физическим признакам.

a – теплопроводность.

Чтобы фигуры были подобны физическим признакам, необходимо,чтобы:

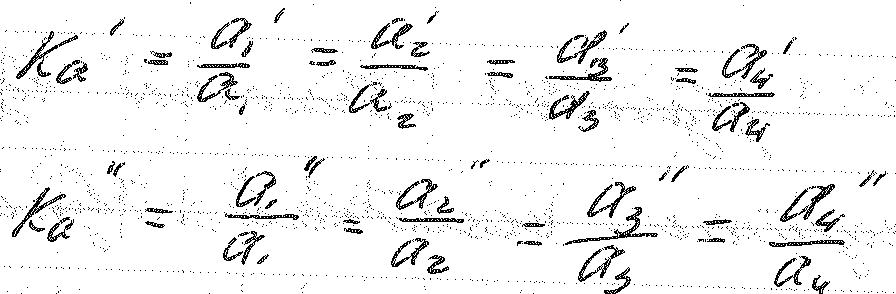
Явления будут подобны, если геометрические, физические и другие признаки сходственные в любые моменты времени.

Сходственность во времени называется - гомохронностью процесса.

Если K_τ =1, то процессы называются – синхронными.

У этих фигур должны быть подобные и начальные условия.

Необходимо подобие и граничных условий. В состав группы входят явления, которые обличают между собой только масштабом.

Теорема Кирпичева:

Подобными называются явления, которые описываются тождественными дифференциальными уравнениями и имеют подобные условия однозначности.

Для подобия необходимо также согласование между явлениями с тем, чтобы первому и второму условию эти явления удовлетворяли бы одновременно.

Множители преобразования выбираются по определенному правилу.