§2. Диффиренциальное уравнение движения вязкой несжимаемой жидкости Новье – Стокса.

Это уравнение выводится на основе 3х законов: закона сохранения энергии, 2ого закона Ньютона и закона Ньютона – Петрова:

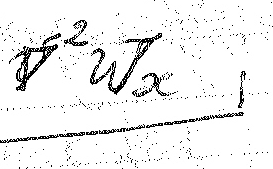
Ρ – плотность жидкости

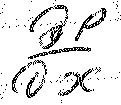- градиент давления вдоль оси x/

q_x – составляющая силы тяжести

μ – коэф. Вязкости

ώ_x – составляющая скорости вдоль оси x

оператор Лапласса по скорости

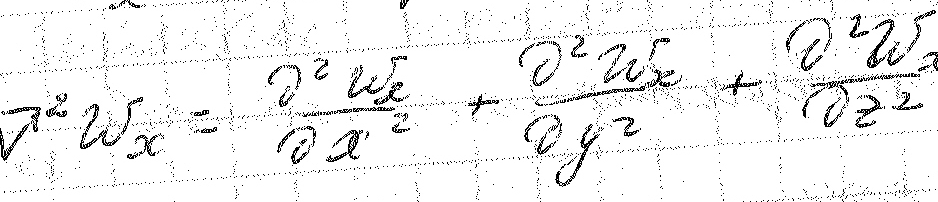
субстационарная производная, характеризующая ускорение жидкости.

Каждый член этого уравнения характеризует силу, отнесенную к единице объема.

- характеризует силу веса

характеризует силу давления

характеризует силу трения

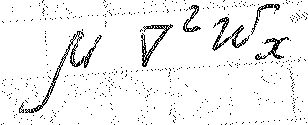характеризует силу инерции.

Знак минус у 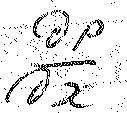указывает, что жидкость перемещается в сторону уменьшения P

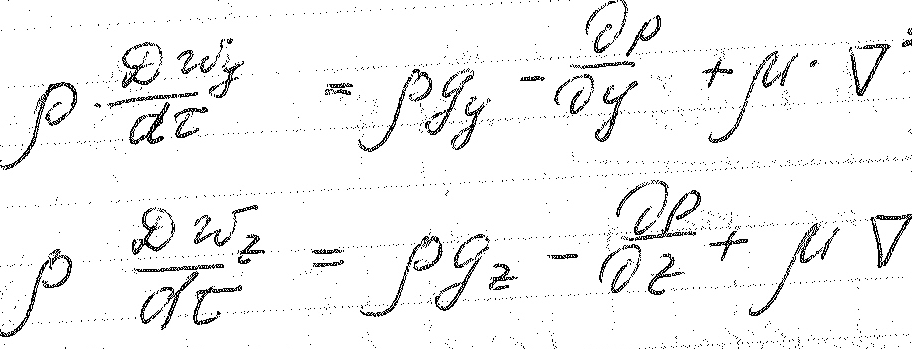
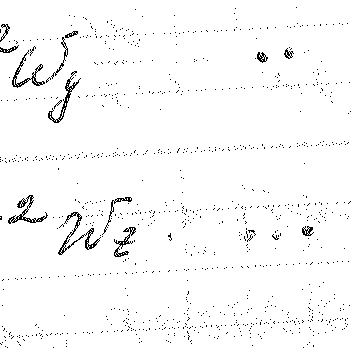
В каждом из уравнений Новье – Стокса содержится две неизвестные – давление и скорость.

Уравнение сплошности или уравнение неразрывности

Это уравнение выводится на основе уравнения сохранения массы.

Для несжимаемой жидкости уравнение сплошности имеет следующий вид:

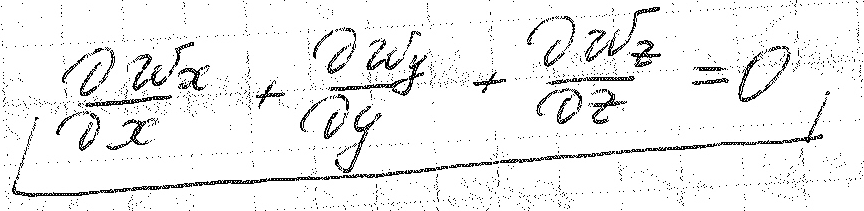
Рассмотренные уравнения представляют собой лишь математическое описание механизма явлений. Поэтому для решения конкретной задачи, которая имеет свою специфику, необходимо эту задачу однозначно определить.

§ 3 Условие однозначности

Условие однозначности определяются из дополнительных сведений,которые носят случайны характер,т.е. которые ни в коей мере не связаны с механизмом процесса.

В состав условия однозначности входят:

1. геометрические свойства, т.е. форма и размеры исследуемого тела или системы тел;

2. физические свойства тел;

3. Начальные условия,которые представляют собой распределение всех зависимых перемещенных,в момент времени, который принимается за начало отсчета.

t( x, y, z, τ)= t₀

Также начальные условия называются временными условиями

4. Необходимы также граничные условия,т.е. условия взаимодействия тела с окружающей средой.

Граничные условия при изучении задачи делятся на 4 рода.

1. Граничные условия первого рода задаются ввиде температуры поверхности исследуемого тела.

t(X, Y, Z, τ) –температура на поверхности.

t(X, Y, Z) = t_пов-ти

2. Граничные условия второго рода.

Задается удельный тепловой поток на поверхности тела, т.е. q(X, Y, Z,τ)

3. Граничные условия третьего рода задаются законом теплообмена тела с окружающей средой. Чаще этот закон задается в виде уравнения Ньютона:

α и tср – задаются..

Условия третьего рода носят универсальный характер. Температура поверхности должна быть определена.

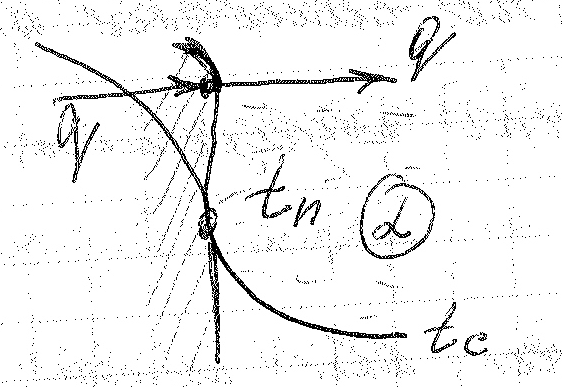
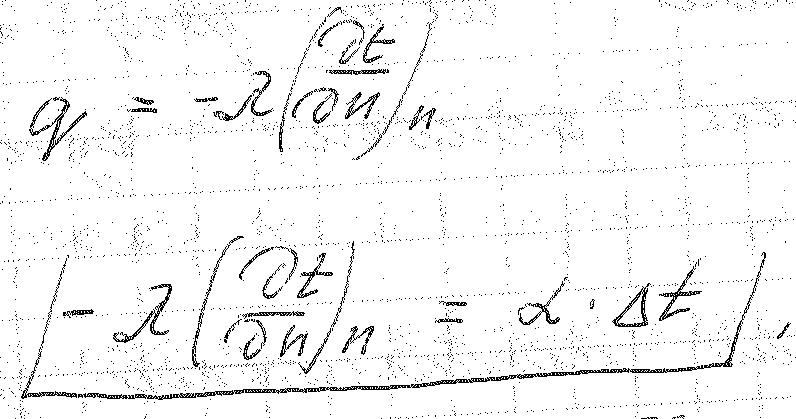
Это дифференциальное уравнение теплообмена граничных условий третьего рода.

4. Граничные условия четвертого рода характерезуют тепловое взаимодействие твердых тел.

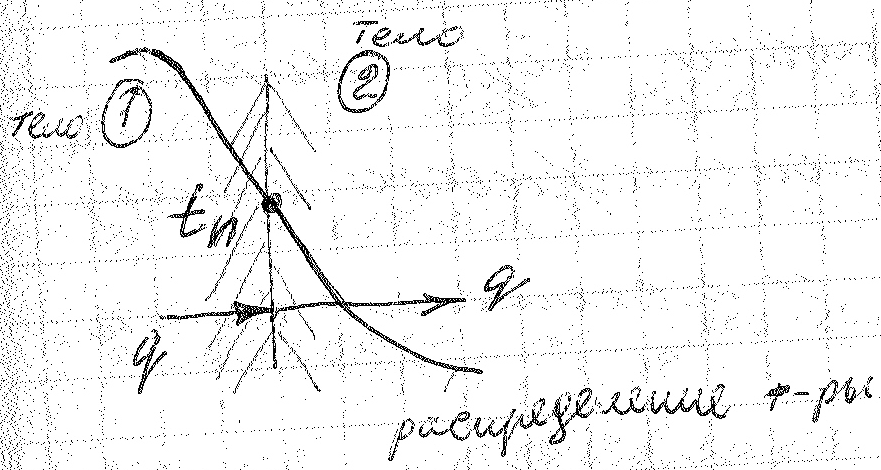
Определим подходящее к телу тепло q по закону Фурье:

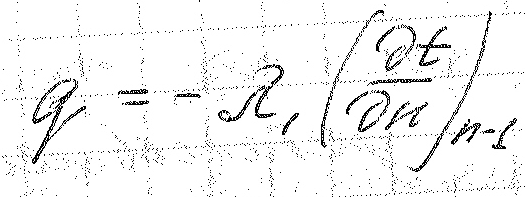
Это же количество тепла мы можем определить следующим образом

Тогда:

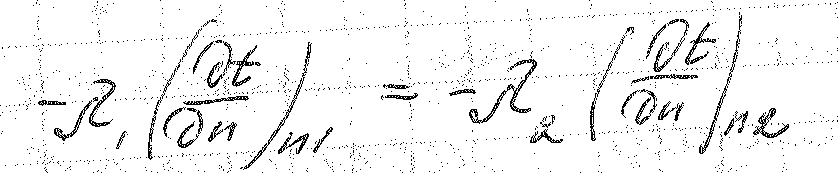
Граничные условия иногда называются пространственными условиями.

В целом геометрические,физические, начальные и граничные условия однозначно определяют задачу.

Математической постановкой задачи является система диференциальных уравнений в совокупности с условиями однозначности.