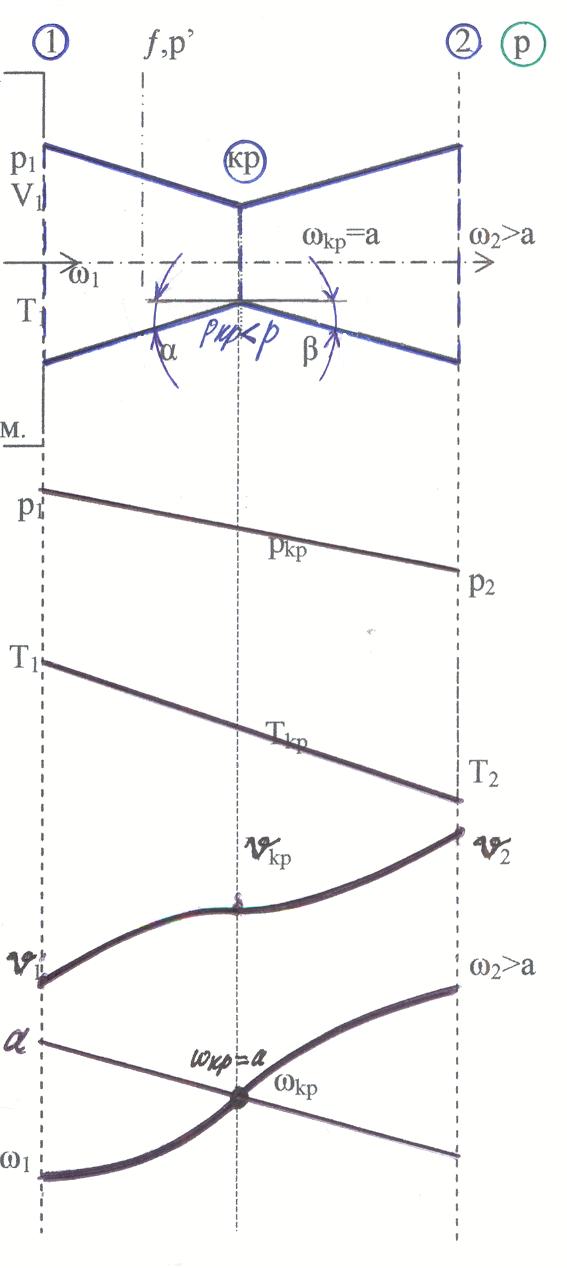
§6 Сопло Лаваля.

a = √kRT

Т.к. температура падает, то и скорость звука падает.

Сопло Лаваля позволяет получать сверхзвуковые скорости истечения газа. При этом расход газа не изменяется и по-прежнему определяется самым узким сечением сопла. Самое узкое сечение сопла называется критическим. Докритический участок - это дозвуковой участок. Закритический - это сверхзвуковой участок.

Профилирование сопла Лаваля.

2k p_{1 2 k+1}

G = ƒ √ k-1 V₁ β ^k - β ^k

p'

β = p₁ ( p’ – давление в рассматриваемом сечении) β = от 1 до 0

G – число заданное [кг/с]

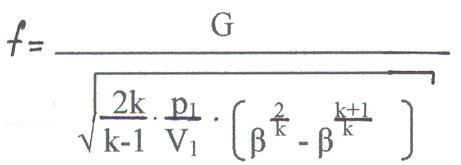
Задавая различные значения β, получаем площадь сечения сопла, в котором давление равно p’ .

Длину сопла по этой формуле не рассчитывают, её определяют экспериментально из условия безотрывного течения газа.

Сопло Лаваля имеет сложную форму по следующим причинам:

ω

G = ƒ∙ v , G – число

G •v = ƒ•ω (a)

Продифференцируем уравнение (а):

Gdv = ƒdω + ωdƒ (б)

Разделим полученное уравнение (б) на исходное уравнение (а):

dv dω dƒ

v = ω + ƒ - уравнение расхода в дифференциальной форме .

dƒ

ƒ - относительное изменение площади поперечного сечения в рассматриваемом сечении.

dv

v - относительное изменение удельного объема в этом сечении.

dω

ω - относительное изменение скорости потока в этом сечении.

dƒ dv dω

ƒ = v - ω

На дозвуковом участке:

dω dv dƒ

ω > v → ƒ < 0 → сопло сужается

В критическом сечении:

dω dv dƒ

ω = v = ƒ =0 → происходит сглаживание

На сверхзвуковом участке:

dω dv dƒ

ω < v → ƒ >0 → сопло расширяется .

В соплах Лаваля можно получить давление р₂ на срезе сопла, равное давлению р в окружающей среде, т.е. полностью понизить давление до давления окружающей среды. Такой режим истечения называется расчетным.

Если давление р₂ понизить до нуля, то поток можно разогнать в 2,5 раза.

59