§3 Цикл Карно в тепловой диаграмме.

T

a b

T₁

T₂

d c

M N s

Определим еще раз термичесикй КПД η_t цикла Карно, используя тепловую диаграмму.

___

q₁=пл.MabN=T₁MN

___

│q₂│=пл.NсdM=T₂MN

(1)

Покажем что в заданном диапазоне изменения температур (Т₁-Т₂), цикл Карно имеет максимальный термический КПД.

Впишем в цикл Карно произвольный цикл ABCD.

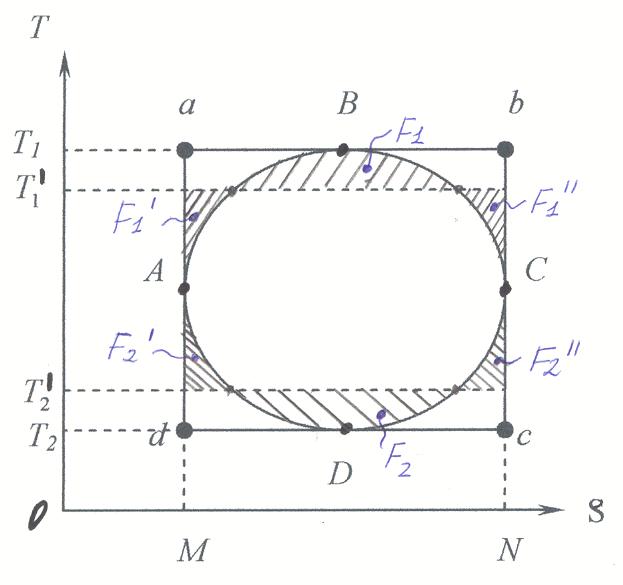
- теплота, подводимая в процессе ABC произвольного цикла.

- теплота, отводимая в процессе CDA произвольного цикла.

Надо показать <

пл.MABCN =

пл.MADCN =

где: - эквивалентные температуры:

-некая условная постоянная температура, при которой подводится та же теплота , что и в процессе ABC.(т.е. площадь F₁=пл. F₁¹+ пл. F₁¹¹=2 пл. F₁¹)

- некая условная постоянная температура, при которой отводится та же теплота , что и в процессе CDA. (т.е. площади F₂=пл. F₂¹+ пл. F₂¹¹=2 пл. F₂¹)

или (2)

Сравним выражение (2) с выражением (1);

; =>

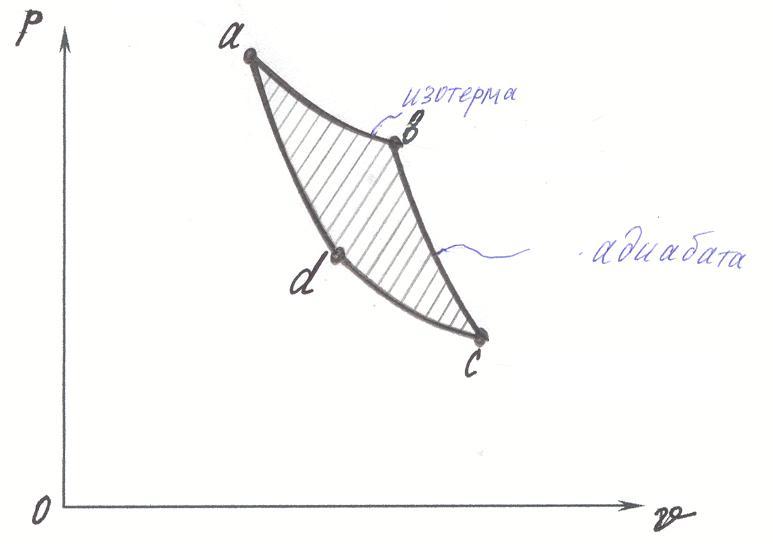
Цикл Карно в рабочей диаграмме:

Цикл Карно не используется не практически, не теоретически, т.к. работа цикла настолько мала, что она сопоставима с работой трения между молекулами газа. Чтобы увеличить работу цикла Карно при заданных R, T­₁, T₂ , необходимо увеличить степень расширения δ, но при этом двигатель получается громоздким (сотни метров).

§4 Энтропия газа.

а ) η_t=1-q₂/q₁

│q₂/T₂│=│q₁/T₁│

b) η_t=1-T₂/T₁

Формулы (а) и (б) определяют термический КПД. Обе они применимы только для цикла Карно.

Учитывая, что q₂ – отрицательная, то можно записать уравнение:

q₂/T₂ + q₁/T₁=0

или: ∑q/T=0 (1)

Это уравнение справедливо только для цикла Карно.

Рассмотрим произвольный цикл в pυ-координатах:

Разобьем цикл Карно рядом адиабат, близко расположенных друг к другу.

Рассмотрим две адиабаты. Произвольный процесс между ними заменим изотермическим процессом. Получим элементарный цикл Карно.

отношение dq/T обозначим как ds.

- интеграл Клазиуса

(2) Cледовательно, энтропия – параметр состояния/