Глава 4. Второй закон термодинамики.
§1 Круговые процессы (циклы).
В предыдущих главах предполагалось, что процесс расширения (сжатия) протекает непрерывно. Однако в действительности процесс расширения, например, протекает до тех пор, пока давление внутри системы не выровняется с давлением в окружающей среде.
Для получения непрерывно работы от газа, необходимо совершить круговой процесс или цикл.
Рассмотрим тепловой процесс в рабочей диаграмме.
р
M a-b
a
l
b
N
A B υ
Пусть точка а характеризует начальное состояние газа. Допустим, что процесс расширения протекает от точки а до точки b по стрелке М.
В этом процессе газ совершает работу равную площади под кривой процесса ab:
lM=пл.AaMbB
Возвратим газ в начальное состояние по стрелке N.
В этом случае над газом совершается работа равная:
lN= пл.BbNaA
Процессы, в которых газ, проходя через ряд промежуточных состояний, возвращается в начальное, называется круговыми процессами(циклами). Очевидно, что разность между lM и lN есть работа за 1цикл равная площади aMbNa.
L=lM-lN=пл.aMbNa
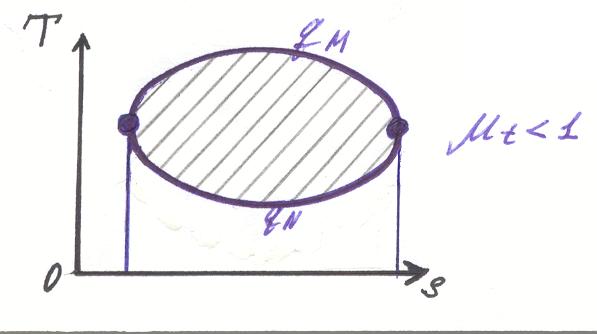
Рассмотрим этот же процесс в тепловой диаграмме.
T
M
a
q
b
N
s
A B
Пусть точка а характеризует начальное состояние газа. Допустим, что процесс подвода тепла происходит от точки а до точки b по стрелке М.
В этом процессе газу подводится теплота, равная площади под кривой процесса аb:
qM= пл. AaMbB
Возвратим газ в начальное состояние по стрелке N. В процессе bNa от газа отводится теплота.
qN=пл.BbNaA;
Очевидно, что разность между qM и qN определяет теплоту, подводимую к газу за цикл:
q=qM - qN=пл.aMbNa .
Связь между работой и теплотой цикла устанавливает I закон термодинамики.
q=Δu+l
Δu=ua-ua=0; q=l
Отсюда => два вывода:
● Площадь циклов в тепловой и рабочей диаграмме равны между собой.
● Направление цикла в рабочей и тепловой диаграмме совпадают.
Если цикл совершается по часовой стрелке, то система(газ) непрерывно совершает работу над окружающей средой за счет теплоты, постоянно подводимой из окружающей среды.
Если цикл совершается против часовой стрелки, то окружающая среда непрерывно производит работу над системой, а система отводит непрерывно тепло в окружающую среду.
Машины, у которых циклы совершаются по часовой стрелке и соответственно теплота преобразуется в работу, называется тепловыми машинами.
Установки, у которых цикл совершается против часовой стрелки и соответственно за счет затраченной извне работой от системы отводится тепло, называются холодильниками.
Совершенство тепловой машины оценивается с помощью термического КПД.
Термическим КПД ηt цикла называется отношение теплоты q, преобразованную в работу l цикла, ко всей подводимой теплоте qM.
ηt=q/qM=l/qM=(qM-qN)/qM=1-qN/qM
Из этой формулы видно, что чем меньше qN тем, больше термическое КПД, и наоборот:
qN↑ => ηt ↓ (qM=const)
