3.3. Функция. График.

Применение методов дифференциального исчислении позволяет проанализировать поведение функции на всей области ее определения. Для проведения такого анализа необхо­димо дать определения критической точки, экстремума функции, точки перегиба и др.

Точка x₀, принадлежащая области определения функции f(x) называется точкой максимума (минимума), если существует та­кое δ > 0, что для любого х ≠ х₀ из интервала (х₀ - δ, х₀ + δ) выполняется неравенство f(х)<f(х₀) (f(x) <f(х₀)).

Точки минимума и максимума называют точками экстре­мума функции.

Необходимое условие экстремума заключается в следую­щем: если точка x₀ является точкой экстремума функции f(х) и в этой точке существует f'(.х), то f'(x) = 0. Точки, в кото­рых f'(x) ⁼ 0, называют критическими точками 1-го рода.

Не все критические точки являются точками экстремума. Рассмотрим достаточные условия экстремума:

1) имеется некоторая функция f(х), непрерывная в точке x₀, для которой в окрестности точки x₀ (х₀ -δ, х₀ + δ), где δ > 0, быть может за исключением самой точки x₀, существует про­изводная f'(x). Если эта производная при переходе через точку х₀:

а) меняет знак с « + » на « - », то точка х₀ является точкой максимума;

б) меняет знак с « - » на « + », то точка х₀ является точкой минимума;

в) не меняет знак, то точка x₀ не является точкой экстремума;

2) имеется некоторая функция f(x), для которой в окрест­ности точки х₀ (х₀ -δ, х₀ + δ), где δ > 0, существуют первая и вторая производные, причем f'(x_Q) = 0, a f"(x₀) ≠0. Тогда:

а) при f"(x₀) < 0 функция имеет максимум;

б) при f"(xо) > 0 функция имеет минимум.

Приведем признаки возрастания и убывания функции. Пусть имеется некоторая дифференцируемая функция f(х). Она бу­дет возрастать (убывать) в некотором интервале (а,b), если ее производная f'(xо) имеет положительный (отрицательный) знак в любой точке этого интервала.

Рассмотрим понятие выпуклости функции. График функции называется выпуклым вверх в интервале (а, b), если он расположен ниже касательной, проведенной к нему в любой точке интервала (a, b). Если график функции лежит выше касательной, проведенной в любой точке рассматрива­емого интервала, то он называется выпуклым вниз в этом ин­тервале

Если функция f(х) имеет первую и вторую производные в интервале (а, b) и f"(x) > 0, то график функции имеет в этом интервале выпуклость вниз, и наоборот, при f"(х) < 0 гра­фик функции обращен выпуклостью вверх.

Точка графика функции f(х), в которой функция непре­рывна и существует касательная, называется точкой перегиба, если при переходе через нее график меняет направление вы­пуклости. Пусть функция f(х) непрерывна и имеет непрерыв­ные первую и вторую производные в интервале (а, b). Тогда в точке перегиба х₀ (а, b) вторая производная равна нулю, причем f"(x₀) при переходе через данную точку меняет свой знак.

Точки, в которых f"(x) = 0, называют критическими точ­ками 2-го рода.

Приведем общую схему исследования функции.

1. Найти область определения функции и, если это воз­можно, определить по виду функции множество ее значений.

2. Определить точки разрыва функции.

3. Найти точки пересечения графика функции с осью абсцисс (у = 0) и осью ординат (х = 0), а также интервалы знакопостоянства функции.

4. Исследовать функцию на четность и нечетность, а так же на периодичность.

5. Найти критические точки 1-го рода. I

6. Определить интервалы возрастания и убывания функции, найти ее экстремумы.

7. Найти критические точки 2-го рода.

8. Определить интервалы выпуклости и найти точки пе­региба.

9. Найти асимптоты.

10. Построить график функции.

Линейная функция

Линейной функцией называется функция вида f (x) =kх + b,

где k и b — некоторые числа.

Свойства линейной функции.

1) Область определения — множество всех действительных чи­сел R.

2) Область изменения (множество значений) при k ≠ 0 — мно­жество всех действительных чисел. При k = 0 множество значений функции состоит из одной точки b.

3) При k ≠ 0 и b ≠ 0 функция не является ни четной, ни нечетной. При k =0 (b — любое) функция четная, при b = 0 и k≠0 — нечетная.

4) Линейная функция непрерывна и дифференцируема на всей числовой оси; ее производная в каждой точке равна k.

5) Линейная функция не имеет экстремумов ни при каких значе­ниях k и b. При k ≠ 0 критических точек нет. При k = 0 каждая точка является критической точкой функции.

6) При k > 0 линейная функция возрастает при всех R, при k < 0 убывает при всех х R, при k = 0 постоянна.

7) График линейной функции пересекает ось Оу в точке у=b. При k≠ 0 график пересекает ось Ох в точке х = —b/k, при k = 0 он параллелен оси Ох.

Обратно пропорциональная зависимость

Переменную у называют обратно пропорциональной переменной х, если значения этих переменных связаны равенством у= k/x, где k — некоторое действительное число, отличное от нуля. Число k называют коэффициентом обратной пропорциональности.

Если считать х независимой переменной, a y — зависимой, то уравнение у = k/x определяет у как функцию от х. График функции у = k/x называется гиперболой,

Свойства функции f (х) = k/x

1) Область определения — множество всех действительных чисел, за исключением числа 0.

2) Область изменения (множество значений) — множество всех действительных чисел, за исключением числа 0.

3) Функция f (х) = k/x— нечетная, и ее график симметричен относительно начала координат. Она непрерывна и дифференцируема во всей области определения; f' (х} = — k/x², критических точек не имеет.

4) Функция f (х) = k/x при k > 0 монотонно убывает на проме­жутках в (— ∞, 0) и (0, + ∞), а при k <0 монотонно возрастает на тех же промежутках.

5) График функции у = k/x при k > 0 в промежутке (0; + ∞) направлен вогнутостью вверх, а в промежутке (— ∞, 0) — вогнуто­стью вниз. При k < 0 промежуток вогнутости вверх — (— ∞; 0), а промежуток вогнутости вниз — (0; + ∞).

Квадратичная функция

Функция f (x) = ах² + bх + с, где а, b, с — некоторые действи­тельные числа (а ≠ 0), называется квадратичной функцией. График квадратичной функции называется параболой.

Свойства квадратичной функции и ее гра­фик.

1) Область определения — вся числовая прямая.

2) При b ≠ 0 функция не является четной к не является нечетной. При b = 0 квадратичная функция — четная.

3) Квадратичная функция непрерывна и дифференцируема во всей области определения.

4) Функция имеет единственную критическую точку х =-b/(2а). Если а > 0, то в точке х = —b/(2а) функция имеет мини­мум. При х < —b/(2а) функция монотонно убывает, при х > —b/(2а) монотонно возрастает.

Если а < 0, то в точке х = —b/(2а) функция имеет максимум. При х < —b/(2а) функция монотонно возрастает, при х > — b/(2а) монотонно убывает.

Точка графика квадратичной функции с абсциссой х_в = -b/(2а) и ординатой у_в=f(x_в) называется вершиной параболы.

5) Область изменения функции: при а > 0—множество значение функции—промежуток (y_в;+ ∞); при а < 0 — множество значении функции — промежуток (-∞;y_в)

6) График квадратичной функции пересекается с осью Оу в точке у = с. В случае, если b² — 4ас > 0, график квадратичной функции пересекает ось Ох в двух точках (различные действительные корни квадратного уравнения); если b²— 4ас = 0 (квадратное уравнение имеет один корень кратности 2), график квадратичной функции ка­сается оси Од: в точке х = — b/(2а); если b² — 4ас < 0, пересечения с осью Ох нет.

График функции симметричен относительно прямой x = —b/(2а).

Степенная функция

Степенной функцией называется функция вида f (х) = х^а, где а — любое действительное число, называемое показателем степени.

Свойства степенной функции.

1)Область определения — множество всех положительных чисел.Область изменения — множество всех положительных чисел.

2)Степенная функция непериодична, не является четной и не является нечетной.

3) Степенная функция непрерывна во всей области определения.

4) Степенная функция дифференцируема во всей области опреде­ления, и ее производная вычисляется по формуле

5) Степенная функция х^а монотонно возрастает во всей области определения при а > 0 и монотонно убывает при а <0.

6) При а < 0 и а > 1 график степенной функции направлен вогнутостью вверх, а при 0 < а < 1 — вогнутостью вниз.

Показательная функция

Показательной функцией называется функция вида f (х) = а^x, где а — некоторое положительное действительное число, называемое основанием степени. При а = 1 значение показательной функции при любом значении аргумента равно единице, и случай а = 1 далее не будет рассматриваться.

Свойства показательной функции.

1) Область определения — вся число­вая прямая.

2) Область изменения (множество зна­чений) — множество всех положительных чисел.

3) Функция непрерывна и дифференци­руема во всей области определения, ее про­изводная вычисляется по формуле (а^x)' =а^х ln а

.

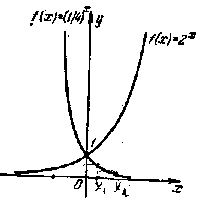
4) При а > 1 функция монотонно возрастает, при а < 1 монотонно убывает.

5) Показательная функция имеет обратную функцию, называемую логарифмической функцией.

6) График любой показательной функции пересекает ось Оy в точке у = 1.

7) График показательной функции — кривая, направленная во­гнутостью вверх.

Логарифмическая функция

Функцию, обратную показательной функции у = а*, называют логарифмической и обозначают y = log_a х.

Число а называется основанием логарифмической функции. Логарифми­ческую функцию с основанием 10 обозначают lg х, а логарифмическую функцию с основанием е обозначают Inх.

Свойства логарифмической функции:

1) Область определения — промежуток (0, +∞).

2) Область изменения (множество значений) — вся числовая прямая.

3) Логарифмическая функция непрерывна и дифференцируема во всей области определения, ее производная вычисляется по формуле

4) Логарифмическая функция монотонно возрастает, если а >1, и монотонно убывает, если 0<а< 1.

5) Графики всех логарифмических функций проходят через точку с координатами (1; 0).

6) При а> 1 график логарифмической функции — кривая, на­правленная вогнутостью вниз; при 0 < а < 1—кривая, направлен­ная вогнутостью вверх.